Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
2
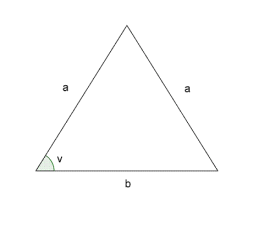
Vi har en rettvinklet, likebeint trekant med kateter lik og hypotenus lik . Den mellomliggende vinkelen mellom og , kalles .
a) Vis at .
b) Hvor stor er ?
c) Finn de eksakte verdiene til og ved hjelp av definisjonene av sinus og cosinus.
3
I en likebeint rettvinklet trekant er katetene 5.4 cm. Regn ut hypotenusen.
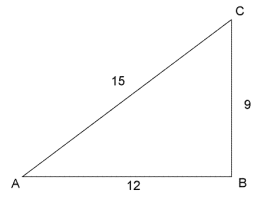
4
a) Bruk Pytagoras' setning til å vise at .
b) Finn de andre vinklene i trekanten.
5
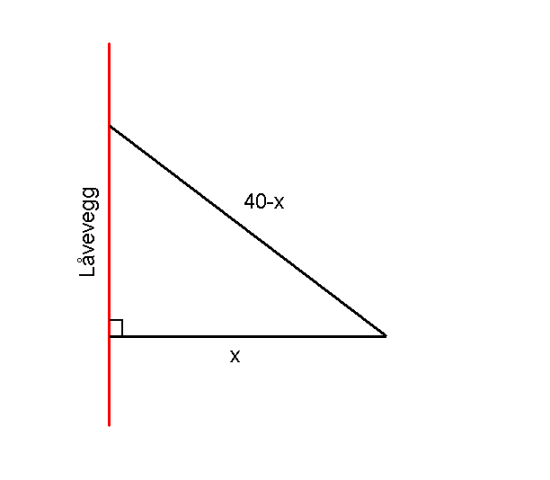
En bonde har m netting-gjerde og skal lage en innhegning for noen høns. Han bestemmer seg for å bruke låveveggen som den ene siden av innhegningen. På grunn av vanskelige grunnforhold med mye stein, ønsker han å bruke bare én påle, og dra nettingen rundt denne. Nettingen skal festes i veggen på to steder, og på det ene stedet, må gjerdet danne vinkel med låveveggen, se figur.
a) Vis at arealet av innhegningen er gitt ved .
b) Finn største mulige areal grafisk på lommeregneren.
6
En sirkel med sentrum S har en radius på 5 cm. Et punkt P ligger 13 cm fra S. En tangent til sirkelen går gjennom P. Hvor langt er det fra P til tangeringspunktet?
7
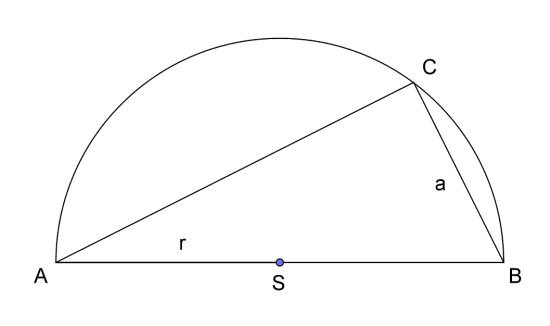
I en sirkel er periferivinkelen ( ) alltid lik halve sentrumsvinkelen ( ).
a) Forklar hvorfor må være rettvinklet.
b) Anta at og at er dobbelt så lang som . Vis at arealet av halvsirkelen unntatt er gitt ved .
8
a) Bruk arealformelen til å vise at arealet av trekanten er .
b) Vis at .
c) Vis at arealet av trekanten også er gitt ved .
9
Regn ut arealet av firkant ABCD der , AB=CD=5 cm og AD = 3cm.
10
Er en trekant med sider 5, 12 og 13 rettvinklet?
Fasit
1
2
b)
c)
3
7.6 cm
4
b) og .
5
b)
6
12 cm
7
a) Sentrumsvinkelen er , så .
b) Pytagoras' setning på gir . Følgelig blir arealet av halvsirkelen . Arealsetningen på trekanten gir at arealet av denne er .
8
9
Tips: I en trekant med vinkler 30o,60o,90o er den minste kateten halvparten av hypotenusen. Firkanten er et parallellogram.
A = 13 cm2
10
Ja