Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
2
3
Den deriverte til en funksjon er gitt ved .
a) Vis at .
b) Bestem nullpunktene til .
c) Bestem i hvilke intervaller vokser og avtar.
4
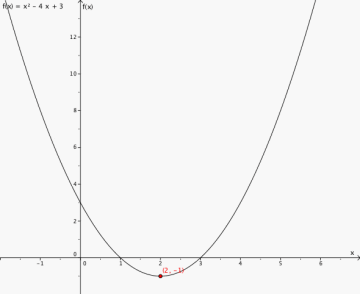
a) Finn bunnpunktet til f.
b) Bestem monotoniegenskapene til f.
c) Tegn grafen til f.
5
Bestem ved hjelp av digitalt verktøy, toppunktet på grafen til
6
7
Finn topp- og /eller bunnpunkt til funksjonen ved regning.
8
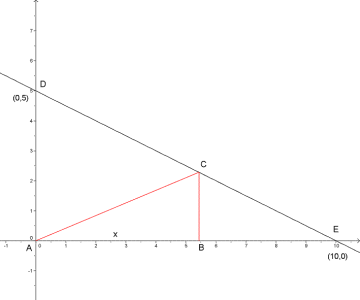
Punktet kan forflyttes langs linjestykket .
a) Vis at arealet av er gitt ved .
b) Hva blir det største arealet trekanten kan ha?
9
f(x)
10
En fastfood-kjede skal lansere en ny hamburger. De er usikre på hvilken pris burgeren bør ha, men den minste prisen den kan ha er kr. Basert på en markedsundersøkelse, tror de at antall solgte burgere per butikk per uke vil avhenge av prisen i tråd med funksjonen
,
der er prisen i kr.
a) Hvor mange burgere blir i gjennomsnitt solgt per butikk på en uke hvis prisen er kr?
b) Anta at det er seks restauranter i kjeden. Sett opp en funksjon som gir inntekten til kjeden per uke når er prisen i kr.
c) Hvilken pris gir maksimal inntekt, og hva blir maksimal-inntekten? Løs grafisk på lommeregneren.
Fasit
1
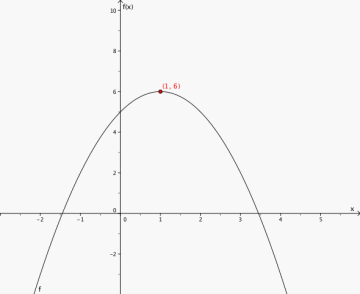
Toppunkt (1,6)
Grafen stiger når x<1
Grafen synker når x>1
2
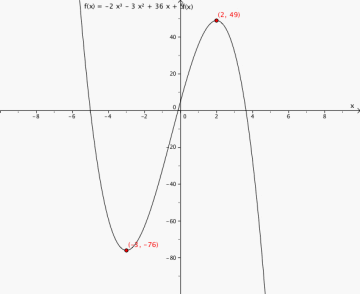
Toppunkt (2,49)
Bunnpunkt (-3,-76)
Grafen synker når x<-3 og når x>2. Grafen stiger når -3
3
b)
c)
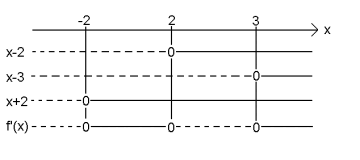
avtar i og i .
vokser i og i .
4
a) (2,-1)
b) minker når x<2, vokser når x>2
c)
5
(0, 25)
6
7
Bunnpunkt: (0,6)
8
b)
9
bunnpunkt: (-0,73, -2,73)
10
a) burgere
b)
c) kr, som gir kr.