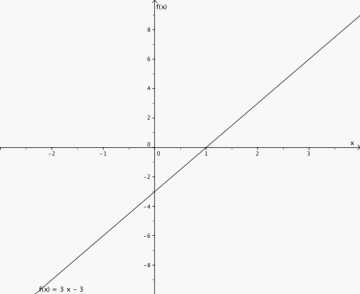Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
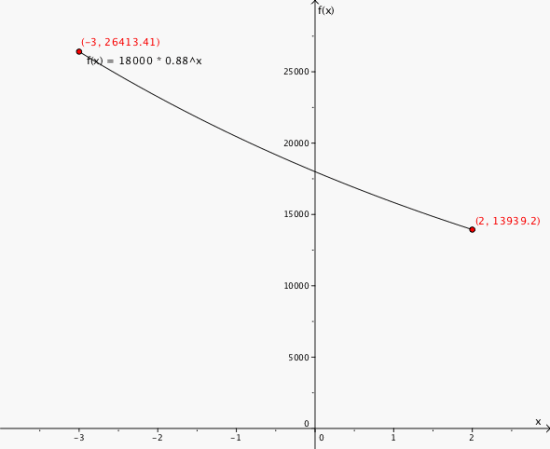
Det årlige verditapet for en moped er 12%. En tre år gammel moped er i år verdt 18 000 kroner.
a) Forklar hvorfor funksjonen f gitt ved er en matematisk modell for verdien av mopeden om x år.
b) Hva kostet mopeden da den var ny?
c) Tegn en graf som viser verdien til mopeden fra den var ny og til den blir fem år. Hvilke forutsetninger har du lagt til grunn for å kunne tegne grafen?
2
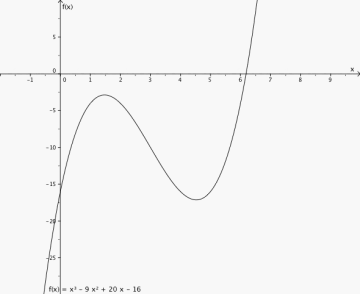
Tegn grafen til følgende tredjegradsfunksjon:
3
La være funksjonen .
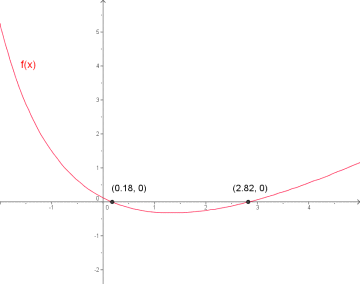
a) Finn nullpunktene til .
b) Finn funksjonsuttrykket for tangenten til grafen til i .
c) Tegn grafen til og tangenten i samme koordinatsystem.
4
f(x)
5
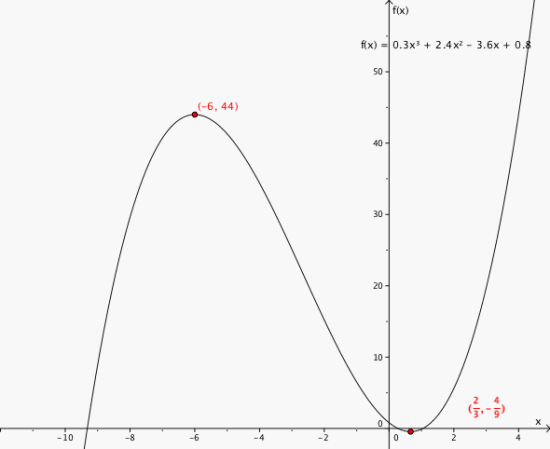
Tegn grafen til f gitt ved .
Bruk grafen til å finne eventuelle topp- og bunnpunkter.
6
Finn egenskaper ved grafen til denne funksjonen:
7
Tegn grafen og bestem veksthastigheten til funksjonen gitt ved
8
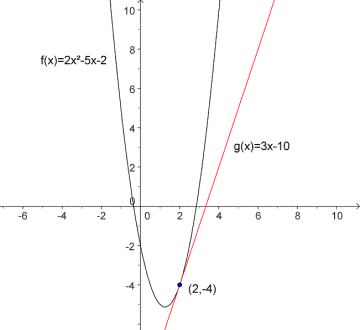
Vi lar være funksjonen .
a) Tegn grafen. Hva er definisjonsmengden og verdimengden ?
b) Vi lar . Hva blir skjæringspunktene mellom og ? Løs grafisk og ved regning.
9
Forklar hvordan grafene til og ligger i forhold til hverandre i samme koordinatsystem. Tegn deretter grafene.
10
Gitt funksjonen .
a) Tegn grafen i intervallet på lommeregneren.
b) Hva er den naturlige definisjonsmengden til funksjonen?
c) Bestem nullpunktene grafisk på lommeregneren og ved regning.
Fasit
1
b) 26 412 kr
c)
2
3
a)
b)
c)
4
5
toppunkt ( - 6 , 44 )
bunnpunkt
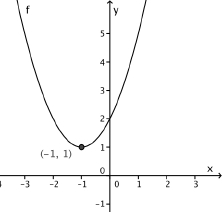
6
Grafen i et koordinatsystem der bunnpunktet (-1, -3) er markert:
7
Veksthastigheten er 3.
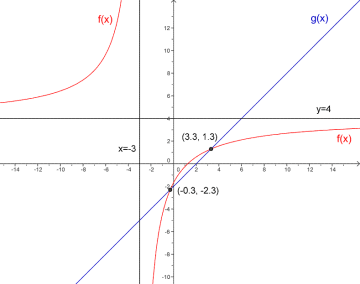
8
a) og
b)
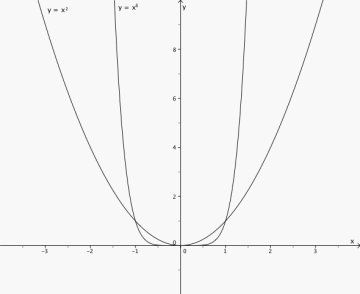
9
For
10
a)
b)
c)