Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Finn hypotenusen når motstående katet er 12 cm og vinkelen er 45o
2
Et tre kaster en m lang skygge på flat mark. Solhøyden er . Hvor høyt er treet?
3
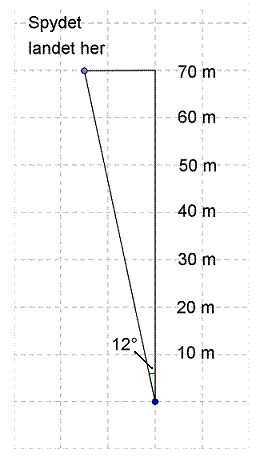
En spydkaster kaster et spyd slik at det danner en vinkel på 12o med aksen til tilløpet. Spydet når akkurat 70 meters-merket på denne aksen, se figuren. Hvor langt er spydkastet?
4
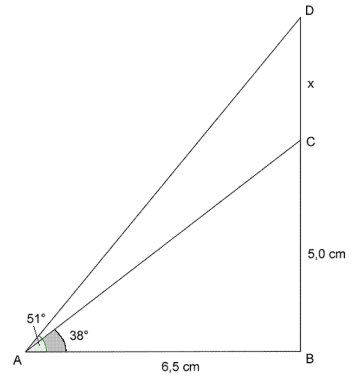
På figuren er og . .
a) Vis at
.
b) Bestem .
5
a) Finn høyden fra C ned på AB.
b) Regn ut arealet av trekanten.
6
I ABC er B = 90°, A = 63° og BC = 71,5 cm.
Finn AB.
7
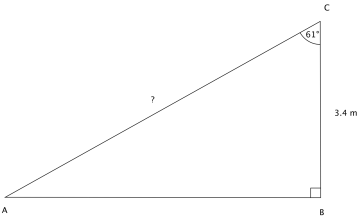
Se figuren og finn lengden av hypotenusen.
8
I trekant ABC er AC = 7,6 cm, vinkel C = 53o og vinkel B = 90o.
Regn ut lengden av sidene AB og BC
9
I ABC er AB= 1,6 cm B = 90° og C = 23°.
Finn AC.
10
a) På en flyplass står to instrumenter i hver sin ende av en rullebane. Rullebanens lengde er kjent. Instrumentene måler vinkelen siktelinja mot et fly danner med bakken. Forklar hvordan denne informasjonen kan brukes til å bestemme flyets høyde.
b) To personer står rett overfor hverandre, men de er på hver sin side av et tårn. De ser begge mot spiret på toppen. Siktelinja til den ene personen danner en vinkel på med bakken, mens siktelinja til den andre personen danner en vinkel på med bakken. Personene står m fra hverandre. Hvor høyt er tårnet?
Fasit
1
17.0 cm
2
m
3
71,56 m
4
b) cm
5
b) 10.5 cm2
6
AB = 34,6 cm
7
7,0 m
8
AB = 6,1 cm og BC = 4,6 cm
9
AC= 4,1 cm
10
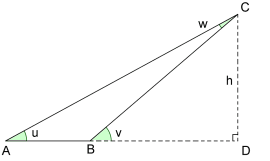
a) På figuren befinner instrumentene seg i punktene og . Flyet er i punkt . Siktelinjene danner vinklene og med bakken. Vi ser at vinkelen . Videre gir sinussetningen . Til slutt får vi, siden er rettvinklet, at .
b) m.