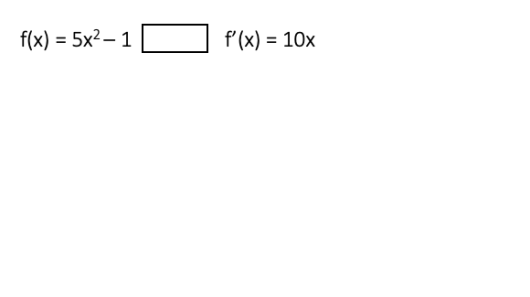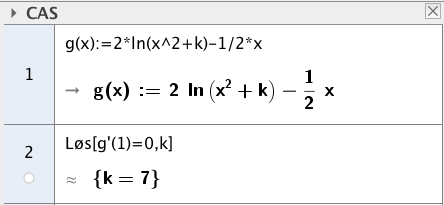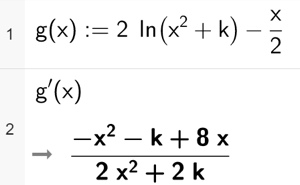Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3022 2017 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler på Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Hjelpemidler på Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 7 oppgaver. Del 2 har 4 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
DEL 1 Uten hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4TBF
Deriver funksjonene
a)
b)
c)
Oppgave 2 (2 poeng) Nettkode: E-4TBJ
Skriv så enkelt som mulig
Oppgave 3 (6 poeng) Nettkode: E-4TBL
Vektorene , og er gitt, der .
a)
Bestem
b)
Bestem
c)
Bestem slik at
d)
Bestem slik at
Oppgave 4 (5 poeng) Nettkode: E-4TBQ
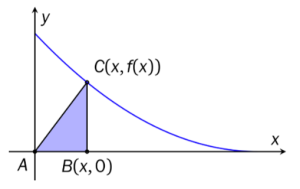
Funksjonen er gitt ved
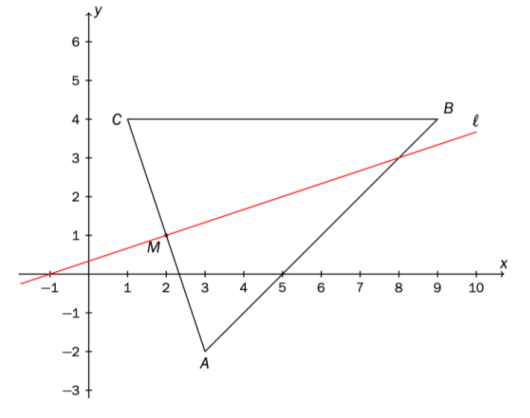
En rettvinklet er gitt ved punktene , og . Se skissen til høyre.
a)
Vis at arealet til kan skrives som
b)
Bestem slik at arealet til blir størst mulig.
c)
Bestem arealet når . Er det andre -verdier som gir dette arealet?
Oppgave 5 (6 poeng) Nettkode: E-4TC8
En nøkkelboks er en boks med plass til nøkler. Noen slike bokser har kodelås.
For én type nøkkelboks lages en kode ved å stille inn fire tall. Hvert tall velges blant tallene til . Et tall kan velges flere ganger. Tallene må være stilt inn i en bestemt rekkefølge.
a)
Hvor mange ulike koder finnes det for denne typen nøkkelboks.
For en annen type nøkkelboks lages en kode ved å velge et bestemt antall forskjellige tall blant tallene til . Tallene trenger ikke å være stilt inn i en bestemt rekkefølge.
b)
Hvor mange ulike koder finnes for denne typen nøkkelboks dersom koden skal bestå av fire forskjellige tall?
c)
Hvor mange tall må koden bestå av for at antallet mulige koder skal bli størst mulig? Hvor mange koder er det da?
Oppgave 6 (7 poeng) Nettkode: E-4TCK
En har hjørnene , og . Punktet er midtpunktet på .
a)
Vis ved vektorregning at har koordinatene .
La være midtnormalen til .
b)
Forklar at
er en parameterfremstilling for .
c)
Avgjør om punktet ligger på .
d)
Bestem koordinatene til skjæringspunktet mellom og midtnormalen til .
Oppgave 7 (3 poeng) Nettkode: E-4TCQ
Nedenfor er det gitt noen utsagn. Skriv av utsagnene. I boksen mellom utsagnene skal du sette inn ett av symbolene , eller . Husk å begrunne svarene.
a)
b)
Oppgave 8 (2 poeng) Nettkode: E-4TCY
Funksjonen er gitt ved
Grafen til har en tangent som går gjennom origo. Bestem likningen for denne tangenten.
DEL 2 Med hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4TD0
Jakob har en spilleliste med sanger på mobilen sin. Fire av sangene på spillelisten er med artisten Kygo. Programmet spiller av sangene i tilfeldig rekkefølge (shuffle) med tilbakelegging. Det vil si at samme sang kan bli spilt at flere ganger etter hverandre.
a)
Forklar at sannsynligheten alltid er for at neste sang som blir spilt, er med Kygo.
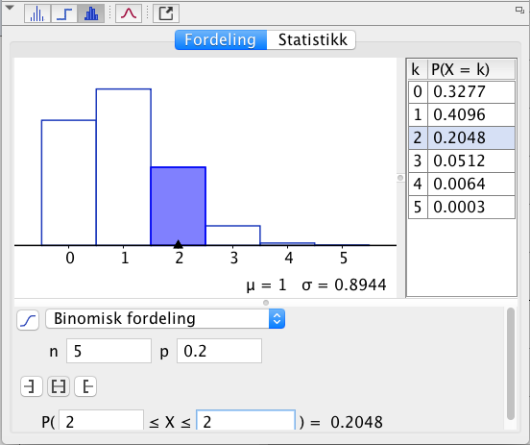
b)
Jakob vil høre på fem sanger fra spillelisten. Bestem sannsynligheten for at nøyaktig to av sangene han spiller, er med Kygo.
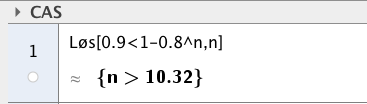
c)
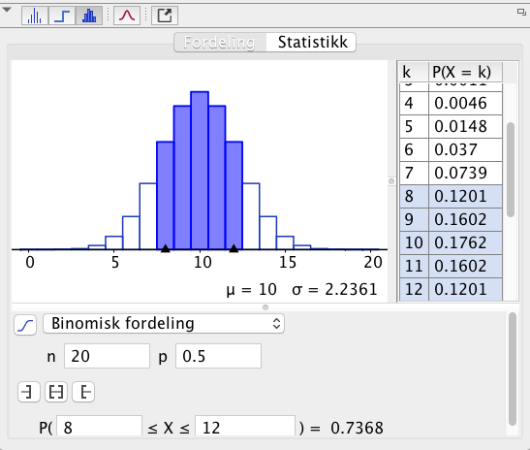
Hvor mange avspillinger må man høre for at sannsynligheten for å få høre minst én sang med Kygo skal være større enn ?
Oppgave 2 (5 poeng) Nettkode: E-4TDU
En har hjørnene , og .
a)
Bestem , og bruk vektorregning til å bestemme .
Tyngdepunktet til en trekant med hjørnene og er generelt gitt ved der er origo.
b)
Bestem, ved vektorregning, koordinatene til tyngdepunktet til .
En er gitt. To av hjørnene er og . Tyngdepunktet er .
c)
Bestem koordinatene til hjørnet .
Oppgave 3 (8 poeng) Nettkode: E-4TE1
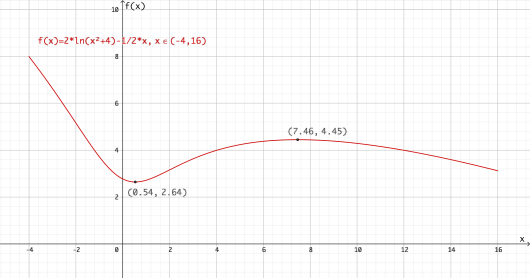
Funksjonen er gitt ved
a)
Bruk graftegner til å tegne grafen når
b)
Bestem eventuelle topp- og bunnpunkt på grafen til .
Funksjonen er gitt ved
c)
Bruk CAS til å bestemme slik at har et ekstremalpunkt i .
d)
Bruk blant annet CAS til å bestemme hvor mange ekstremalpunkt har for ulike verdier av .
Oppgave 4 (6 poeng) Nettkode: E-4TEA
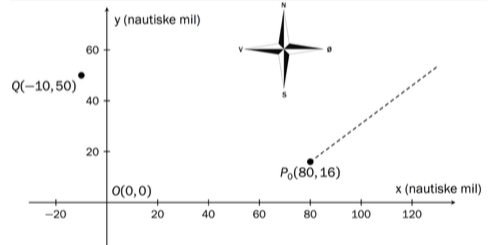
 Skipet Euler sender ut en melding om at det har fått motorstopp. Kapteinen oppgir at posisjonen er i et bestemt koordinatsystem. På grunn av driften vil posisjonen (i nm) i timer senere være gitt ved
Skipet Euler sender ut en melding om at det har fått motorstopp. Kapteinen oppgir at posisjonen er i et bestemt koordinatsystem. På grunn av driften vil posisjonen (i nm) i timer senere være gitt ved
a)
Hvilken fartsvektor driver skipet med? Hvor stor er farten (banefarten)?
En redningsbåt som ligger i , sier at den er klar til å gå mot skipet og kan være ved Euler om timer.
b)
Hvor stor fart holder redningsbåten?
En annen redningsbåt er i posisjonen når meldingen blir sendt. Den kan holde en fart på nm/h.
c)
Bruk CAS til å bestemme hvor lang til det vil gå før denne redningsbåten kan være framme ved Euler.