
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2015 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 8 oppgaver. Del 2 har 7 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4CR5
| Dag | Temperatur |
| Mandag | |
| Tirsdag | |
| Onsdag | |
| Torsdag | |
| Fredag | |
| Lørdag |
Tabellen ovenfor viser hvordan temperaturen har variert i løpet av noen dager.
Hva må temperaturen være på lørdag dersom medianen av målingene skal bli 7 °C ?
Løsningsforslag
Jeg tenker
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi setter opp de forskjellige temperaturene i stigende rekkefølge.
Vi skal plassere et tall på denne skalaen slik at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
der er temperaturen på lørdag. Medianen av tallene over er gjennomsnittet av de to midterste tallene, altså og . Hvis medianen skal være , må derfor være lik .
Svar: Temperaturen på lørdagen må være .
Mer om
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Medianen er den verdien som vi finner i midten av et rangert datamateriale. Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Tabell

Median
Statistikk
For flere eksempler og forklaringer se artikkelen Median.
For å øve mer, se oppgavesettet om median i Treningsleiren.
Oppgave 2 (1 poeng) Nettkode: E-4CR7
En vare koster i dag 240 kroner. Prisen er da satt ned med 20 %.
Hvor mye kostet varen før prisen ble satt ned?
Løsningsforslag
Jeg tenker:
Hvis prisen er satt ned til kroner, så er kroner av originalprisen.
Vi ser at er av originalprisen. Med andre ord, vi har at Det betyr at originalprisen må være kroner. Vi vet at , så dette er lik så originalprisen var .
Svar:
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Prosent
For flere eksempler og forklaringer se artikkelen Regneregeler.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
Oppgave 3 (2 poeng) Nettkode: E-4CR9
Forskere antar at universet er ca. 14 milliarder år gammelt.
a)
Skriv 14 milliarder på standardform.
Løsningsforslag a)
Jeg tenker:
Én milliard er . Vi skal skrive det som et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Et tall på standardform er på formen der er et tall mellom og , og er et heltall.
Vi har at millard er , så milliarder er . Dette er nesten på standardform, bortsett fra at tallet før tierpotensen ikke er mellom og . Vi vet at , så
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Svar:
Mer om:
Denne oppgaven er om Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3... Symbolet for mengden av hele tall er ℤ. En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Standardform
Heltall
Potens
Eksempel:
For flere eksempler og forklaringer se artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.
b)
I ett år er det ca. 32 millioner sekunder.
Omtrent hvor mange sekunder gammelt er universet? Skriv svaret på standardform.
Løsningsforslag b)
Jeg tenker
Vi må
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.
Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Én million er , så millioner er . Dette er cirka antall sekunder i året. Universet er cirka år gammelt, og det er sekunder. Vi regner ut for hånd.
| 3 | 2 | 4 | = | 8 | ||||||
| 1 | 2 | 8 | ||||||||
| 3 | 2 | |||||||||
| 4 | 4 | 8 |
Vi ser at , så universet er sekunder gammelt.
Svar: sekunder
Mer om
Denne oppgaven er om Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Standardform
Potens
Eksempel:
For flere eksempler og forklaringer se artiklene Oppsummering av regneregler for potenser og Multiplikasjon av desimaltall.
For å øve mer, se oppgavesettene multiplikasjon og tall på standardform i Treningsleiren.
Visste du at
Her har vi uttrykt et ufattelig stort tall på veldig liten plass. Dette viser styrken til tall på standardform, og hvorfor det er mye brukt i for eksempel astrofysikk.
Oppgave 4 (2 poeng) Nettkode: E-4CRC
Regn ut
a)
Løsningsforslag a)
Jeg tenker
Vi ser en brøk med
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Vi regner ut
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen.
Svar: Det blir
Mer om
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Brøk

For flere eksempler og forklaringer se artikkelen Oppsummering av regneregler for potenser.
For å øve mer, se oppgavesettet om potensregning i Treningsleiren.
b)
Løsningsforslag b)
Jeg tenker
Vi ser en
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Vi tar
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Svar:
Mer om
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Eksponent
xn = x · x · x...· x, n gangerGrunntall
Brøk

For flere eksempler og forklaringer se artiklene Rask gjennomgang av regneregler for potens og røtter og Karoline bruker potensregler.
For å øve mer, se oppgavesettet om potensregning i Treningsleiren.
Oppgave 5 (2 poeng) Nettkode: E-4CRF
Antall elever ved en skole har avtatt lineært de siste 10 årene. For 10 år siden var det 1 400 elever ved skolen. Nå er det 1 340 elever ved skolen.
a)
Bestem en modell som viser utviklingen disse 10 årene.
Løsningsforslag a)
Jeg tenker:
Vi skal lage en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Vi lar være antall år etter år siden, og være antall elever i år . Det vil for eksempel si at er antall elever ved skolen for 8 år siden, og er antall elever i dag. Det vi skal gjøre er å finne en
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Svar: Hvis er antall elever for år siden, er .
Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Linje
For flere eksempler og forklaringer se artikkelen Å lage en matematisk modell.
For å øve mer, se oppgavesette om lineære funksjoner i Treningsleiren.
b)
De neste årene regner en med at antall elever vil avta med 0,5 % per år.
Bestem en modell som viser hvor mange elever det vil være ved skolen om år.
Løsningsforslag b)
Jeg tenker:
Hvis noe avtar med en viss prosentandel hvert år, så kan vi modellere det med en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vi kan modellere dette med en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Hvis er antall elever ved skolen år etter i år, så er .
Mer om:
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Eksponentialfunksjon

Vekstfaktor
Prosent
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Eksempel: Antall bakterier i en gryte.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleiren.
Oppgave 6 (6 poeng) Nettkode: E-4CRK
| Alder | Frekvens |
| 10 | |
| 20 | |
| 30 | |
| 40 |
Tabellen ovenfor viser aldersfordelingen for lærerne ved en skole.
a)
Bestem gjennomsnittsalderen for lærerne ved skolen.
Løsningsforslag a)
Jeg tenker:
Vi arbeider med gruppert informasjon. Da antar vi at dataene vi har er jevnt fordelt innenfor gruppene.
At vi antar at dataene er jevnt fordelt innenfor gruppene, betyr at for eksempel gjennomsnittalderen av alle som er i intervallet er
Tabellen lister opp aldersgrupper på venstre side, og
Frekvens
Frekvensen er resultatet av å dele det totale antallet ganger en hendelse intereffer i løpet av et bestemt tidsintervall på intervallets lengde.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: Gjennomsnittsalderen er år.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger. Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennGjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
Tabell

For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
b)
Lag et histogram som viser aldersfordelingen for lærerne.
Løsningsforslag b)
Jeg tenker:
Her må vi huske på at det siste aldersintervallet er dobbelt så stort som de andre.
Det aller første vi gjør, er å tegne opp et passende
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.

Nå skal vi lage søylene våre. I aldersgruppen er det lærere. Det betyr at vi skal lage en søyle som har grunnflate (fordi det er så stort aldersintervallet er), og den skal ha areal (fordi det er lærere i denne aldersgruppen). Da må høyden til søylen være . Tilsvarende må høyden på søylene til aldersgruppene og være henholdsvis og . Det siste intervallet, , er derimot dobbelt så stort som de forrige. Vi skal lage en søyle som har som grunnflate, og areal . Da må søylen ha høyde . Resultatet er vist under.
Svar: 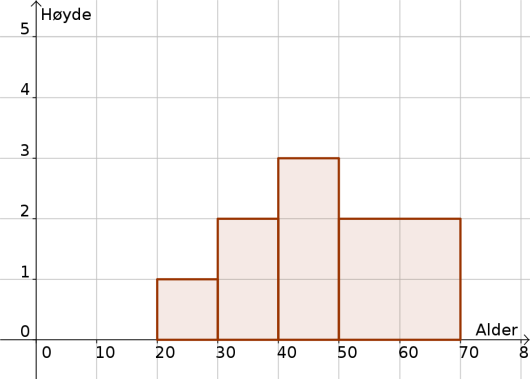
Mer om:
Denne oppgaven er om Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). Den horisontale aksen i et koordinatsystem. Den loddrette aksen i et koordinatsystem. Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Koordinatsystem

x-akse

Kalles også førsteakse.y-akse

Kalles også andreaksen.Histogram
Statistikk
For flere eksempler og forklaringer se artikkelen Histogram.
c)
Utvid tabellen med en kolonne som viser relativ frekvens, og en kolonne som viser kumulativ frekvens.
Løsningsforslag c)
Jeg tenker
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Det aller første vi gjør, er å skrive ned den nye tabellen vi skal fylle ut.
| Alder | Frekvens | Relativ frekvens | Kumulativ frekvens |
|---|---|---|---|
| 10 | |||
| 20 | |||
| 30 | |||
| 40 |
Vi starter med de
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
| Alder | Frekvens | Relativ frekvens | Kumulativ frekvens |
|---|---|---|---|
| 10 | |||
| 20 | |||
| 30 | |||
| 40 |
Så skal vi regne ut de
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Svar:
| Alder | Frekvens | Relativ frekvens | Kumulativ frekvens |
|---|---|---|---|
| 10 | 10 | ||
| 20 | 30 | ||
| 30 | 60 | ||
| 40 | 100 |
Mer om
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Antall observasjoner av en spesiell hendelse dividert på antall observasjoner. Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Tabell

Relativ frekvens
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.Kumulativ frekvens

Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
Oppgave 7 (6 poeng) Nettkode: E-4CRR
Karl står på balkongen og kaster en ball opp i lufta. Etter sekunder er ballen tilnærmet
meter over bakken, der
a)
Fyll ut tabellen nedenfor
| 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | |
| 18,75 | 18,75 | 8,75 |
Løsningsforslag a)
Jeg tenker
Her skal vi regne ut verdien til
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Det første vi gjør er å skrive av tabellen.
| 0 | 1 | 2 | 3 | ||||
Nå starter vi utfyllingen. Under der står, skal vi skrive verdien til . Det gjør vi ved å sette inn i uttrykket for . Da får vi Vi skriver dette inn i tabellen.
| 0 | 1 | 2 | 3 | ||||
| 15 |
Videre skal vi regne ut , og . Det gjør vi på helt tilsvarende måte som over. Vi fåraltså , og . Vi fyller dette inn i tabellen som vist under.
Svar:
| 0 | 1 | 2 | 3 | ||||
| 15 | 20 | 15 | 0 |
Mer om
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og .Funksjon
Tabell

Polynom
For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
b)
Tegn grafen til .
Løsningsforslag b)
Jeg tenker
Her kan vi tegne inn punktene fra tabellen inn i et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Det første vi gjør er å tegne et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Nå skal vi tegne inn punktene fra tabellen. Under i tabellen står det . Det betyr at , altså at er et punkt på grafen til . Vi tegner av en prikk på dette stedet i koordinatsystemet. På tilsvarende måte skal vi tegne av prikker i punktene , , og så videre.

Til slutt skal vi tegne grafen som går mellom disse prikkene. Vi prøver å gjøre kurven så jevn som mulig, og tegner derfor ikke rette streker mellom punktene. Resultatet er vist under.
Svar: 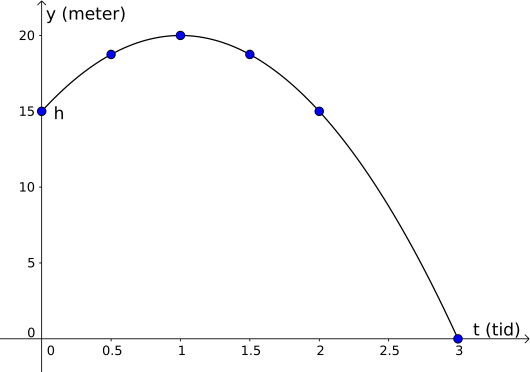
Mer om
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).Tabell

Punkt

Graf
Funksjon
Koordinatsystem

For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
c)
Gi en praktisk tolkning av verdiene av og .
Løsningsforslag c)
Jeg tenker
Her må vi bruke teksten, og huske på at er ballens høyde over bakken etter sekunder.
Tallet er hvor høyt ballen var over bakken idet Karl kastet den. Karl stod på en balkong, og dette betyr at balkongen var cirka meter høy. Videre er ballens høyde over bakken etter sekunder; denne høyden er , og det betyr at ballen har truffet bakken. Med andre ord tok det sekunder fra ballen ble kastet til den traff bakken.
Svar: Ballens starthøyde, og omtrentlig balkongens høyde, var meter. Siden traff ballen bakken sekunder etter den ble kastet.
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Graf
Koordinatsystem

Funksjon
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?.
Oppgave 8 (3 poeng) Nettkode: E-4CRV
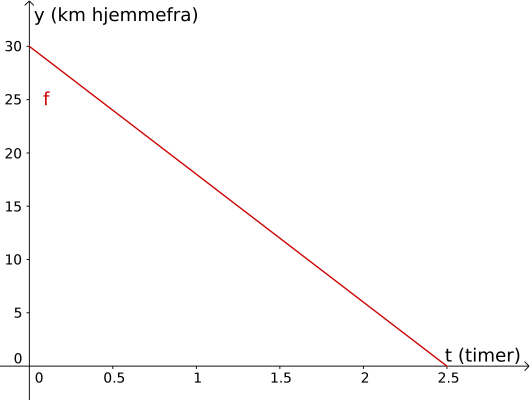
Sigurd er 30 km fra hjemmet sitt. Han sykler hjemover med en konstant fart på 12 km/h.
Lag en grafisk framstilling som viser sammenhengen mellom antall timer og antall kilometer han er hjemmefra.
Hvor lang tid tar det før han kommer hjem?
Løsningsforslag
Jeg tenker
Her er det lurt å tegne en
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Vi skal tegne
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
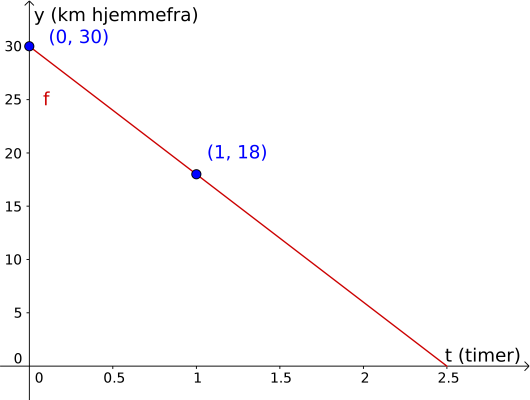
Vi kan se direkte at likningen til linjen er , fordi
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Fart
Fart er tilbakelagt distanse per tidsenhet.
Fart måles ofte i km/h, som leses kilometer per time, eller m/s som leses meter per sekund.
Når noe beveger seg veldig raskt, kan det være hensiktsmessig å bruke km/s.
Videre skal vi finne ut hvor lang tid det tar før Sigurd kommer hjem. Sigurd er hjemme når han er kilometer i avstand fra hjemmet sitt, altså der . På grafen vår ser vi helt tydelig at der , altså bruker Sigurd 2 timer og 30 minutter på hjemreisen. Vi kunne også løst dette problemet ved å løse likningen , altså Vi legger til på begge sider og dividerer på . Da får vi akkurat som før.
Svar: Sigurd brukte timer og minutter på hjemreisen, gitt at han syklet i retningen rett mot hjemmet sitt.
Mer om
Denne oppgaven er om Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). Den loddrette aksen i et koordinatsystem. Lineære funksjoner er funksjoner som er skrevet på formen . Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Koordinatsystem

y-akse

Kalles også andreaksen.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Stigningstall

Graf
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.
DEL 2 Med hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4CRX
Per, Pål og Espen skal låne 3 000 kroner hver. Lånene skal betales tilbake etter seks måneder. De får følgende betingelser:
- Per får tilbud om å betale tilbake 3 450 kroner etter seks måneder.
- Pål får tilbud om en månedlig rente på 2,2 %.
- Espen får tilbud om en månedlig rente på 1,8 % og et etableringsgebyr på 100 kroner.
Gjør beregninger, og avgjør hvem som får det beste tilbudet.
Løsningsforslag
Jeg tenker
Her må vi regne ut hvor mye hvert av lånene koster totalt.
Vi regner ut hvor mye penger man må betale totalt. Det første lånet, altså lånet til Per, koster ganske enkelt kroner. Pål har en månedlig rente på . Etter måneder, blir det totale beløpet Pål må betale, lik Dette er litt mindre enn det Per måtte betale. Espen betaler i månedlig rente, men med et etableringsgebyr på kroner. Derfor må Espen betale totalt Dette er mindre enn Per, men ikke like lite som Pål. Derfor fikk Pål det beste tilbudet.
Svar: Pål fikk det beste tilbudet. (Pål betalte , mens Per og Espen betalte henholdsvis og .)
Mer om
Denne oppgaven er om Renter er prisen du betaler for å låne penger, eller det du tjener dersom du låner ut penger. Se renteformel og rentefot Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Rente
Prosent
For flere eksempler og forklaringer se artikkelen Renter.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
Oppgave 2 (4 poeng) Nettkode: E-4CS0
Tabellen nedenfor viser antall kvinnelige studenter i Norge noen utvalgte år.
| År | 2001 | 2003 | 2005 | 2007 | 2009 | 2011 | 2013 |
| Antall kvinnelige studenter |
53553 | 58237 | 59562 | 63292 | 62957 | 68391 | 73332 |
La svare til år 2000, til år 2001, og så videre.
a)
Bruk opplysningene i tabellen til å bestemme en lineær modell som viser hvordan antall kvinnelige studenter har utviklet seg i denne perioden.
Løsningsforslag a)
Jeg tenker
En
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Først lager vi et regneark med tallene vi har. Dette gjør vi ved å velge «Regneark» i «Vis»-menyen, og å skrive inn punktene. I den første kolonnen skriver vi -verdiene tilsvarende årene i tabellen, altså , , og så videre, som representerer , , og så videre. I neste kolonne skriver vi antall kvinnelige studenter i Norge i de gitte årene. Vi markerer tallene vi har skrevet, og velger «Liste med punkt» i «Lag»-menyen. Listen blir hetende «Liste1». Nå kan vi finne en lineær modell ved å skrive kommandoen
RegLin[Liste1]i «Skriv inn»-vinduet. Da får vi opp en linje, og den har likning Dette er den lineære modellen vår.
Svar: Den lineære modellen er .
Mer om
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner er funksjoner som er skrevet på formen .Regresjon
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Regresjon 1.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.
b)
Hvor stor har økningen i antall kvinnelige studenter vært i gjennomsnitt per år i denne perioden?
Løsningsforslag b)
Jeg tenker
Her skal vi se på
Proporsjon
Proporsjon betyr at to forhold er like.
Eksempel: a forholder seg til b som c forholder seg til d,
Fra til økte antall kvinnelige studenter med Denne økningen skjedde over år, så gjennomsnittlig økning er studenter per år. Vi kunne også sett dette ved å tegne linjen mellom det første og siste punktet i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
En annen mulighet for å estimere gjennomsnittlig økning, vil være å bruke stigningstallet til den lineære modellen vi fant i deloppgave a). I så fall ville vi svart . Dette tallet vil være en bedre estimator på hvordan ting har vært og hvordan det vil utvikle seg videre. Dette svaret vil også være mer robust enn
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: Gjennomsnittlig økning var studenter i året.
Mer om
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Linje
Stigningstall

Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.
c)
Anta at denne utviklingen fortsetter i årene som kommer.
I hvilket år vil antall kvinnelige studenter passere 85 000?
Løsningsforslag c)
Jeg tenker
Her er det usikkert om vi skal bruke den første
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi har funnet likningen til den lineære modellen i a). Hvis antall kvinnelige studenter hadde økt med samme gjennomsnittøkning som i perioden mellom og , ville den lineære modellen vært linjen som gikk gjennom punktene og . Å finne ut når antall kvinnelige studenter passerer , tilsvarer å finne
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
y = 85000i GeoGebra, og å markere krysningspunktene som vist under.
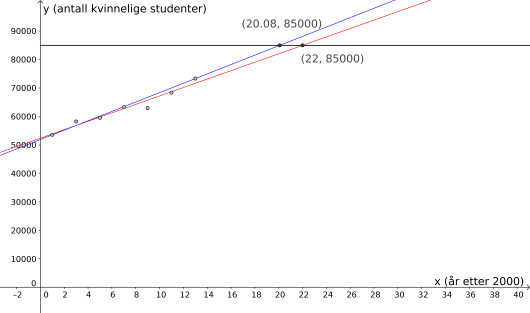
På bildet er den røde linjen den lineære modellen vi fant i a), mens den blå linjen viser hva som skjer hvis vi følger den gjennomsnittlige økningen i b). I følge modellen i a) vil antall kvinnelige studenter passere når , altså i 2022; i følge modellen i b) vil det skje i .
Svar: I følge modellen i a) vil antall kvinnelige studenter passere i , og i følge den gjennomsnittlige veksten i b) vil det skje i .
Mer om
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Skjæringspunkt

Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Linje
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artiklene Grafisk løsning av likninger og Eksempel: Når koker vannet?.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Oppgave 3 (3 poeng) Nettkode: E-4CS4
Tallene nedenfor viser temperaturen målt i grader celsius klokka 16 den 30. juni de siste 20 årene i by A.
20 18 20 19 19 21 20 22 22 18 17 18 22 19 21 20 22 22 21 17
a)
Bruk regneark til å bestemme gjennomsnitt og standardavvik for datamaterialet.
Løsningsforslag a)
Jeg tenker
Her kan vi bruke regneark i Excel.
Det første vi gjør er å skrive ned alle tallene i en kolonne i regnearket. Vi har brukt Excel.
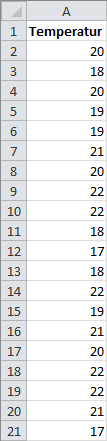
For å regne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
=GJENNOMSNITT(A2:A21)og
=STDAV.P(A2:A21)henholdsvis. Resultatet er vist under.
Svar: Vi har brukt formlene
=GJENNOMSNITT(A2:A21)og
=STDAV.P(A2:A21)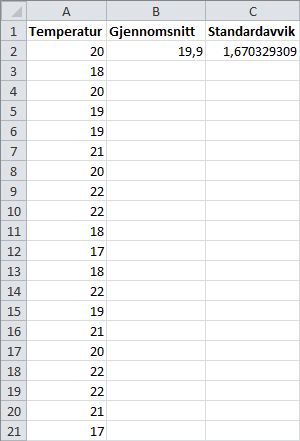
Mer om
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger. Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Funksjon
Statistikk
Standardavvik
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
For flere eksempler og forklaringer se artikkelen Varians og standardavvik.
b)
Tilsvarende data er samlet inn i by B. Gjennomsnittet her er 20,8 °C , og standardavviket er 3,4 °C.
Noen planlegger et større utearrangement 30. juni neste år og er avhengige av varmt vær. Arrangementet skal finne sted enten i by A eller i by B.
Hvilket råd vil du gi arrangørene ut fra de oppgitte dataene?
Løsningsforslag b)
Jeg tenker
By B har høyere gjennomsnittstemperatur, men også høyere standardavvik.
Fordi
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Svar: By A gir mer forutsigbarhet i temperaturen, mens by B gir høyere gjennomsnittstemperatur.
Mer om
Denne oppgaven er om Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger. Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.Statistikk
Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Standardavvik
For flere eksempler og forklaringer se artiklene Gjennomsnitt, median og typetall og Varians og standardavvik.
Oppgave 4 (7 poeng) Nettkode: E-4CS8
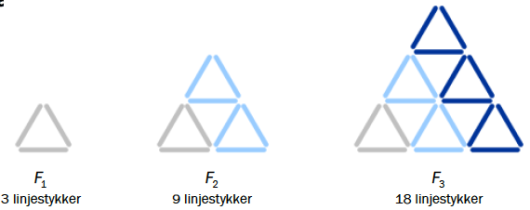
Ovenfor ser du tre figurer , og . Tenk deg at du skal fortsette å lage figurer etter samme mønster.
a)
Hvor mange linjestykker vil det være i ?
Løsningsforslag a)
Jeg tenker
Vi må legge til
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
Vi ser at hver figur er den samme som forrige figur, men tillagt en rad med trekanter. For å få legger man til trekanter, og man legger til trekanter til for å komme videre til . For å komme til legger man derfor til trekanter. Hver trekant har linjestykker i seg, så derfor må vi legge til linjestykker for å komme fra til . Figur har allerede linjestykker i seg, som skrevet i oppgaven, og da blir antall linjestykker i lik .
Svar: linjestykker
Mer om
Denne oppgaven er om En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Linje
Trekant

For flere eksempler og forklaringer se artikkelen En trekant.
b)
Forklar hvordan antall linjestykker endrer seg fra figur til figur, og lag et regneark som gir en oversikt over antall linjestykker i de 20 første figurene , , ...,
Løsningsforslag b)
Jeg tenker
I hver figur må vi legge til nok trekanter til å fylle opp en ny rad.
For å komme fra figur til figur , må vi legge til nye trekanter, som hver har linjestykker i seg. Det betyr at hvis er antall linjestykker i figur og er antall linjestykker i figur , så er For eksempel ser vi at , og da må , og , akkurat som i henholdsvis figur og figur .
Dette kan vi representere i et regneark. Vi fører opp en tabell over antall linjestykker i hver figur. I den første figuren er det linjestykker.
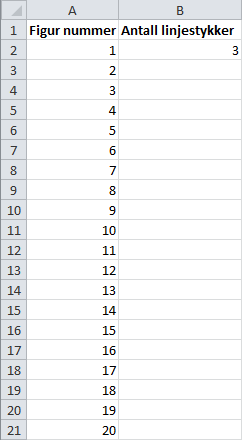
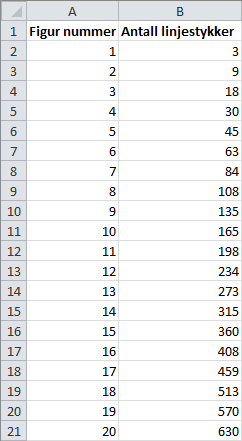
Vi kan regne ut antall streker i figur ved hjelp av , akkurat som over, bare ved hjelp av regnearket. Vi bytter ut i formelen med ruten der antall linjer i forrige figur står, i dette tilfellet B2, og vi bytter ut med tallet i kolonnen til venstre og opp, altså A2. Vi skriver det følgende i rute B3:
=B2 + 3*(A2 + 1)Denne prosedyren skal vi gjøre for de resterende figurene også, og vi kan gjøre det enkelt ved å “dra” boksen B3 ned til B21. Se resultatet under.
Svar: Hvis er antall linjestykker i figur , så er ..
Mer om
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Tabell

Linje
Trekant

For flere eksempler og forklaringer se artikkelen Parenteser i et regnestykke.
c)
Antall linjestykker i figur kan skrives som et andregradsuttrykk.
Bruk regresjon til å bestemme dette andregradsuttrykket.
Løsningsforslag c)
Jeg tenker
Her skal vi bruke
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
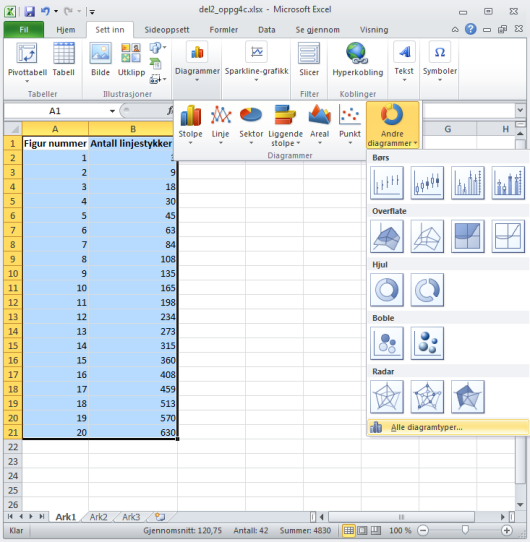
I det nye vinduet velger vi «Punkt» og deretter velger bildet med bare punkter på som vist under.
Vi får da opp en graf med punktene våre, men vi vil også lage en trendlinje og derfor høyreklikker vi og velger «Legg til trendlinje...».
Velg «Polynom» blant valgmulighetene. Dette betyr at vi vil finne et
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Vi får da opp en linje som passer til punktene og funksjonsuttrykket til linja.
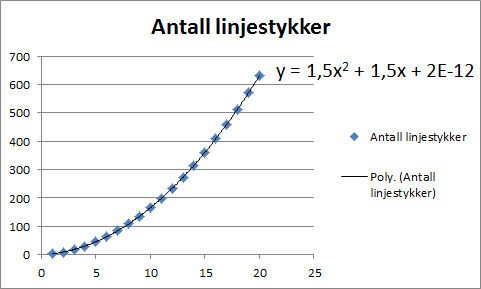
Fordi funksjonen angir antall linjestykker, må gi og derfor er antall linjestykker i figur gitt ved .
Svar: Figur har linjestykker.
Mer om
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. Den horisontale aksen i et koordinatsystem. Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Regresjon
x-akse

Kalles også førsteakse.Andregradsuttrykk
Linje
Graf
For flere eksempler og forklaringer se artikkelen Regresjon 1.
Visste du at:
I denne oppgaven startet vi med likningen og fant at vi kunne uttrykke bare ved hjelp av , uten å måtte regne ut først. Likningen over er et eksempel på en differenslikning, og vi sier at uttrykket er løsningen til differenslikningen. Vi merker oss her at løsningen på likningen ikke er et tall, men en likning i seg selv. Mange ting i naturen kan modelleres ved hjelp av differenslikninger, for eksempel veksten av kaniner som formerer seg. Et kjerneeksempel på en differenslikning er den kjente Fibonacci-tallrekken, der neste tall i rekken er summen av de to foregående, og vi starter med 1. Rekken blir 1, 1, 2, 3, 5, 8, 13, og så videre. Vi kan representere dette som en differensligning på følgende måte:Her har vi fått med et ledd , som vi ikke hadde i vår oppgave. På grunn av dette leddet kalles ligningen over for en differensligning av andre grad. Løsningen til ligningen er (overraskende nok)Tallet kalles ofte det gylne snitt, og man skriver gjerne den greske bokstaven når man refererer til tallet (på samme måte som at man skriver for ). Det gylne snitt er en historie for seg selv.
d)
Bruk andregradsuttrykket du fant i oppgave c) til å bestemme hvor mange linjestykker det vil være i
Løsningsforslag d)
Jeg tenker
Her kan vi sette inn i
Formel
En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.
Eksempel: , er en formel for flateinnholdet av en sirkel med radius r.
Fra deloppgave c) vet vi at figur har linjestykker. Derfor må ha akkurat som vi fikk i b).
Svar:.
Mer om
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.Funksjon
Andregradsuttrykk
For flere eksempler og forklaringer se artikkelen Andregradsfunksjoner.
Oppgave 5 (6 poeng) Nettkode: E-4CSD
Du skal kjøpe ny sykkel, og du vil forsikre den. Dersom sykkelen blir stjålet, må du betale 2000 kroner i egenandel på forsikringen.
Anta at sykkelen koster kroner som ny. Dersom sykkelen blir stjålet før det har gått et år, vil du få utbetalt kroner i erstatning fra forsikringsselskapet. Erstatningen avtar med 10 % per år.
a)
Forklar at er en modell for mye du får utbetalt dersom sykkelen blir stjålet etter år.
Løsningsforslag a)
Jeg tenker
Erstatningen avtar med hvert år, så
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
La oss si at sykkelen ble stjålet etter år. Den opprinnelige erstatningen man skulle fått er nå redusert med , fra til . Dette er det samme som . Hvis den hadde blitt stjålet etter år, ville vi fått i erstatning. Generelt, hvis sykkelen blir stjålet etter år, så vil vi fåi erstatning. Derfor er en god modell.
Svar: Vekstfarten til erstatningen er , så om sykkelen ble stjålet etter år hadde vi fått kroner i erstatning.
Mer om
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Eksponentialfunksjon

Vekstfaktor
Prosent
For flere eksempler og forklaringer se artikkelen Hva er prosent?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
b)
Du velger å kjøpe en sykkel som koster 10 000 kroner.
Hvor mye får du utbetalt dersom sykkelen blir stjålet etter 7 år?
Løsningsforslag b)
Jeg tenker
Her kan vi bruke formelen vi fikk i deloppgave a).
Fra deloppgave a) vet vi at hvis sykkelen ble stjålet etter år, så hadde vi fått kroner i erstatning, der er det sykkelen kostet som ny. I vårt tilfelle kostet sykkelen ny, og den ble stjålet etter 7 år, så og . Da får vi kroner i erstatning.
Svar: Cirka kroner
Mer om
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? .Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Prosent
For flere eksempler og forklaringer se artikkelen om Typer av funksjoner.
c)
For å forsikre sykkelen må du betale 150 kroner i forsikringspremie per år. Anta at sykkelen blir stjålet etter år.
Sett opp en modell som viser hvor mye du totalt sitter igjen med når du tar hensyn til det du har betalt i forsikringspremie i løpet av disse årene.
Løsningsforslag c)
Jeg tenker:
Vi må finne ut hvor mye vi har betalt i premie i årene før sykkelen ble stjålet.
Her må vi tolke hva som menes med at sykkelen blir stjålet etter år. Vi tolker det som at sykkelen er år gammel når den blir stjålet. Hvis den blir stjålet første året, er . Hvis den blir stjålet det andre året er . Det tilsvarer altså at den stjeles etter år.
Vi må betale forsikring en gang i året, første gang når vi kjøper sykkelen. Etter ett år betaler vi forsikringspremie for . gang. Etter 2 år betaler vi forsikringspremie for . gang og så videre. Etter år, eller når sykkelen blir år gammel, betaler vi forsikringspremie for gang nummer .
Totalt innbetalt premie hvis sykkelen stjeles etter år blir
kroner. Utbetalt erstatningssum blir
kroner. Når vi tar hensyn til innbetalt premie, får vi en erstatning på
kroner.
Svar: Modellen er der er hvor mye sykkelen kostet da den ble kjøpt. Hvis sykkelen kostet som ny, ville vi sittet igjen med kroner.
Mer om:
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Hva er matematisk modellering?.
d)
Din venn Ronny mener at du bør si opp forsikringsavtalen etter 13 år.
Ta utgangspunkt i modellen du fant i oppgave c) og kommenter Ronnys utsagn.
Løsningsforslag d)
Jeg tenker:
Vi antar at sykkelen kostet kr, altså er og vi må finne ut hvor mye penger vi sitter igjen med hvis sykkelen ble stjålet etter år.
Dersom sykkelen stjeles etter 13 år, altså mens den er 13 år gammel, vil forskjellen mellom det vi får utbetalt og det vi totalt har betalt for forsikringen være
kroner. Dersom sykkelen stjeles mens den er 12 år gammel, blir denne forskjellen
kroner.
Ronny tenker antakelig at han vil få utbetalt mer enn han totalt sett har betalt i forsikringspremie hvis sykkelen stjeles før den har blitt 13 år gammel. Stjeles den etter at den har blitt 13 år gammel, vil han ha betalt inn minst kroner mer i forsikringspremie enn han har fått utbetalt i erstatning. Han ønsker derfor ikke å forsikre sykkelen etter at den har blitt 13 år gammel.
Idet sykkelen blir 13 år gammel må vi avgjøre om vi skal forsikre den for det kommende året. Alle tidligere innbetalinger gjelder en tjeneste vi allerede har fått, nemlig forsikring for alle de foregående årene. Det er kun fremtiden vi bør tenke på når vi vurderer forsikring. Derfor bør vi se på følgende: Sykkelens verdi, erstatningssum, forsikringspremie, sannsynligheten for at sykkelen blir stjålet i løpet av det neste året og egen evne til å erstatte et eventuelt tap av sykkelen.
Her er det lett å beregne erstatningssum. Denf finner vi fra uttrykket i oppgave a), og vil være
kroner. Spørsmålet er om vi vil betale kroner for å kunne få kroner utbetalt hvis sykkelen blir stjålet mens den er 13 år gammel. Hvis sykkelen ikke har blitt stjålet de 13 første årene, og kanskje ikke har blitt mer attraktiv i årenes løp, er sannsynligheten for at den blir stjålet antakelig liten. Det er gode argumenter for at de kronene som kunne gått til forsikring heller bør investeres i noe annet.
Svar: Det er gode argumenter for at de 150 kronene som kunne gått til forsikring heller bør investeres i noe annet.
Mer om:
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Eksponentialfunksjon

Tabell

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Eksempel: Når koker vannet?.
Oppgave 6 (6 poeng) Nettkode: E-4CSI
Funksjonen gitt ved
viser temperaturen grader celsius i sjøen et sted på Sørlandet dager etter
31. desember 2013.
a)
Bruk graftegner til å tegne grafen til .
Løsningsforslag a)
Jeg tenker:
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi skal bruke kommandoen
Funksjon[ <Funksjon>, <Start>, <Slutt> ]i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
f = Funksjon[-0.0000028*x^3+0.001*x^2-0.025*x+3.8, 0, 300]Her må vi stille inn GeoGebra på desimaler for å kunne se funksjonsuttrykket i algebrafeltet. Videre må vi tilpasse
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Svar: 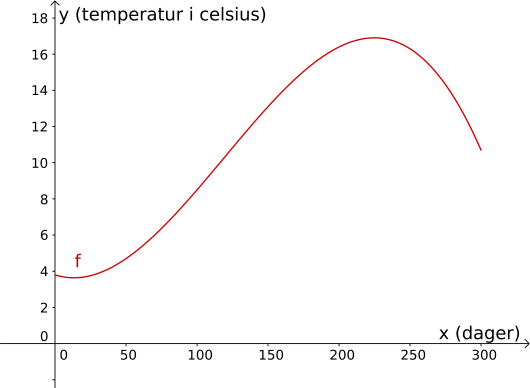
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Funksjon
Polynom
Graf
For flere eksempler og forklaringer se artikkelen Fra en funksjon til en graf. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet grafisk framstilling i Treningsleiren.
b)
Bestem forskjellen mellom høyeste og laveste temperatur.
Løsningsforslag b)
Jeg tenker:
Høyeste og laveste temperatur er -koordinatene til henholdsvis
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Ekstremalpunkt[f]i «Skriv inn»-vinduet i GeoGebra-filen fra deloppgave a). Kommandoen «Ekstremalpunkt» ser bare på ekstremalpunkter i det indre av definisjonsmengden. Det kunne tenkes at funksjonen oppnår større eller lavere verdier i endepunktene for intervallet enn de verdiene vi har funnet med kommandoen. Vi ser på grafen at det ikke er slik. Funksjonsverdiene for nær eller nær er mellom de verdiene vi fant med kommandoen «Ekstremalpunkt». Hadde høyre endepunkt for definisjonsmengden vært i stedet for , ville vi fått lavest temperatur etter dager.
Da ser vi at bunnunktet har koordinater , og at toppunktet har koordinater . Dette betyr at etter rundt 13 dager så var temperaturen , og etter rundt 225 dager var temperaturen . Forskjellen mellom den høyeste og den laveste temperaturen er
Svar: Forskjellen er .
Mer om:
Denne oppgaven er om En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall. Eksempler: og . En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt . Funksjon
Polynom
Graf
Ekstremalpunkter
Toppunkt

Bunnpunkt

For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.
c)
Bestem og den momentane vekstfarten til når . Hva forteller disse svarene?
Løsningsforslag c)
Jeg tenker:
For å finne må vi sette inn i uttrykket for . Vi kan bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
For å finne , skriver vi ganske enkelt
f(100)i «Skriv inn»-vinduet i GeoGebra. Da får vi . Det betyr at temperaturen i sjøen var da det hadde gått dager.
Så skal vi finne den
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
(100,f(100))Videre trykker vi på «Tangenter» i menyen med linjer. Deretter velger vi punktet vårt, og grafen . Tangenten er vist under.
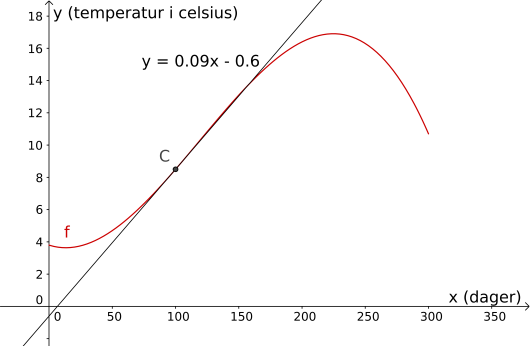
Her ser vi at tangentlinjen har likning . Det betyr at den momentane stigningen til i er . Dette forteller oss at etter dager, så vil temperaturen øke med cirka per dag.
Svar: , så temperaturen i sjøen var da det hadde gått dager. Den momentane vekstfarten til der var , så etter dager, økte temperaturen med cirka per dag.
Mer om:
Denne oppgaven er om Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet. Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Lineære funksjoner er funksjoner som er skrevet på formen . En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Tangent

Momentan vekstfart
Funksjon
Graf
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Ligning
Derivasjon
For flere eksempler og forklaringer se artikkelen Introduksjon til derivasjon - gjennomsnittlig og momentan vekstfart.
For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.
Visste du at
Der er også mulig å finne momentan vekstfart ved regning. Dette gjøres på følgende måte. La oss si at vi vil finne den momentane vekstfarten til en funksjon der , for eksempel og . Først velger vi oss et annet punkt på grafen til , for eksempel . Så finner vi ligningen for linjen som går gjennom disse to punktene; dette kan vi gjøre på den vanlige måten vi har lært. Det vi gjør videre, er å flytte dette nye punktet nærmere og nærmere . Da vil likningen for linjen mellom punktene bli mer og mer lik tangetlinjen i . Dette er vist på bildet under; de stiplede linjene er linjen mellom de to punktene, og den røde linjen er tangentlinjen.
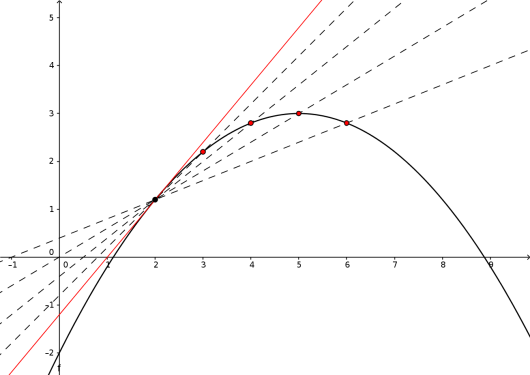
Stigningstallet til linjene vil altså tilnærme seg den momentane vekstfarten. Men selv om vi gjør dette ganger, så vil ikke stigningstallet være helt likt den momentane vekstfarten – derfor må vi bruke det som kalles grenseverdier. Hvis du vil vite mer om grenseverdier, og det å finne momentan vekstfart ved hjelp av disse, burde du først lese lynkurset i grenseverdier og deretter lynkurset i derivasjon.
For mer om grenseverdier, se lynkurset Grenseverdier.
Oppgave 7 (6 poeng) Nettkode: E-4CSN
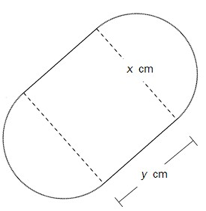
Tenk deg at du skal lage en boks. Bunnen og toppen av boksen skal være satt sammen av et rektangel og to halvsirkler og ha form som vist på figuren ovenfor. Sideflaten skal stå vinkelrett på topp og bunn. Sett bredden i rektanglet lik cm, lengden lik cm og høyden lik cm.
a)
Forklar at volumet av boksen er gitt ved
Løsningsforslag a)
Jeg tenker
Boksen er et
Prisme
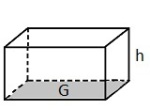
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.
Har et prisme grunnflate G og høyde h, er volumet lik G · h.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
der er arealet til grunnflaten av boksen og er høyden. (Vi dropper enheten cm for enkelhets skyld.) Vi har ikke tallverdier for , og , men vi kan late som om vi har det, og regne med dem som vanlige tall likevel. Grunnflaten består av et
Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Arealet til begge halvsirklene til sammen er derfor , og arealet til hele grunnflaten er
Dette kan vi sette inn i likningen
og vi får at
akkurat som vi ville ha.
Svar: er arealet til grunnflaten, og multipliserer vi med høyden får vi volumet.
Mer om
Denne oppgaven er om Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene. En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk. Eksempel: , er en formel for flateinnholdet av en sirkel med radius r. Sirkel brukes i to betydninger: 1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets. Areal: En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Volum

Areal
Noen måleenheter for areal er m2, dm2 og cm2.Geometri
Formel
Sirkel

2) Flaten som sirkellinjen begrenser.
Omkrets: Ligning
For flere eksempler og forklaringer se artikkelen Et rett prisme.
For å øve mer, se oppgavesettet om volum i Treningsleiren.
b)
Summen av lengden og bredden i rektanglet skal være 10 cm, og summen av bredden og høyden skal være 5 cm.
Forklar at og , og bruk dette til å sette opp et uttrykk for volumet av boksen uttrykt med .
Løsningsforslag b)
Jeg tenker
Summen av lengden i
Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
Vi har at og . I den første likningen kan vi trekke fra på begge sider, og forkorte. Da får viPå samme måte trekker vi fra på hver side av likningen , og vi får , som var det vi ville ha.
Nå skal vi bruke det vi har funnet til å sette opp et uttrykk for volumet bare uttrykt ved . Det gjør vi ved å sette inn og i likningen for
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Dette er volumet uttrykt kun ved . Vi kunne multiplisert ut parentesene, men det blir ikke spurt etter i oppgaven.
Svar: .
Mer om
Denne oppgaven er om En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°. Omkrets: Ligning
Funksjon
Volum

Rektangel

Areal:
For flere eksempler og forklaringer se artiklene Et rektangel og Lineære likninger.
For å øve mer, se oppgavettet om førstegradslikninger i Treningsleiren.
c)
Bruk graftegner til å bestemme hvor bred boksen må være for at volumet skal bli størst mulig. Hvor stort blir volumet da?
Løsningsforslag c)
Jeg tenker
Vi kan tegne
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
I forrige oppgave fant vi ut at hvis bredden til boksen er , så er
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
(Det å skrive i stedet får , betyr bare at størrelsen avhenger av . Det betyr ingenting annet. Men nå kan vi tenke på som en funksjon: Hvis bredden til boksen er , så setter vi inn i funksjonsuttrykket vårt, og volumet til boksen blir .)
Vi kan tegne grafen til med
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
V(x) = (pi*(0.5*x)^2 + x*(10-x))*(5-x)i «Skriv inn»-vinduet, og tilpasser aksene slik at vi ser hele grafen. For å finne toppunktet til grafen, skriver vi ganske enkelt kommandoen
Ekstremalpunkt[V]Da ser vi at
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
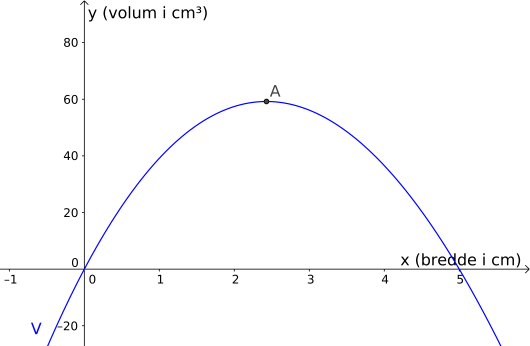
Hvis vi går lenger ut i grafen til , ser vi at funksjonen får veldig store verdier; mye større enn . Disse verdiene er ikke interessante. Det er fordi hvis , så er , og det har ingen fysisk tolkning at boksen har negativ høyde.
Svar: Boksen har størst volum, på , når bredden til boksen i centimeter er .
Mer om
Denne oppgaven er om Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3). En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Vi sier at et punkt er et ekstremalpunkt for en funksjon hvis det enten er et toppunkt eller bunnpunkt for funksjonen. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemVolum

Funksjon
Graf
Ekstremalpunkt

Toppunkt

Koordinat
For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.




