
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2013 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Doruller: http://pub.tv2.no/multimedia/TV2/archive/00950/First_price_950599i.jpg (21.10.2012)
- Andre bilder, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4BUZ

En kveld kjørte en taxisjåfør 10 turer.
Nedenfor ser du hvor mange passasjerer han hadde med på hver av turene.
1 5 3 3 5 2 1 4 1 2
a)
Bestem medianen, gjennomsnittet og typetallet for dette datamaterialet.
Løsningsforslag a)
Jeg tenker:
Denne oppgaven er om
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
For å finne
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Videre skal vi finne gjennomsnittet av tallene. Gjennomsnittet er
eller sagt på en annen måte, forholdet mellom summen av tallene over og antall tall. Sjåføren kjørte 10 turer til sammen, og gjennomsnittet blir derfor(Her har vi valgt bruke tallene satt opp i stigende rekkefølge, for da kan det være lettere å regne ut summen.)
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Svar: Medianen er , gjennomsnittet er og typetallet er 1.
Mer om:
Denne oppgaven er om
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Typetall
Typetallet er det tallet som opptrer flest ganger i et innsamlet tallmateriale fra for eksempel en spørreundersøkelse.
Eksempel: 1, 1, 2, 2, 2, 3, 3, 4, 4, 5. Her er typetallet 2.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere eksempler og forklaringer se artikkelen Gjennomsnitt, median og typetall.
For å øve mer, se oppgavesettet om median, gjennomsnitt og typetall i Treningsleieren.
b)
Sett opp en tabell som viser frekvens og kumulativ frekvens for antall passasjerer på turene.
Løsningsforslag b)
Jeg tenker:
Frekvens
Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.
Se frekvenstabell
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Vi skal sette opp en
Frekvenstabell
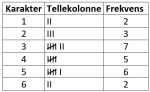
En frekvenstabell er en opptelling og ordning av dataene i en datasamling.
Se frekvens
Frekvens
Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.
Se frekvenstabell
| Antall passasjerer | Frekvens | Kumulativ frekvens |
|---|---|---|
Videre skal vi finne
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
| Antall passasjerer | Frekvens | Kumulativ frekvens |
|---|---|---|
Dette gjør vi for alle de andre tallene også. Vi merker oss at kumulativ frekvens for vil være kumulativ frekvens av pluss frekvensen til , for da får vi med alle turene det har vært med eller færre passasjerer. Dermed kan vi finne alle de kumulative frekvensene ved å se på frekvens-kolonnen og det vi tidligere har oppført i den kumulative frekvens-kolonnen. Den kumulative frekvensen for er , for er den , for er den , for er den , og for er den . Vi fyller dette inn i tabellen. Den ferdige tabellen er vist under.
Svar:
| Antall passasjerer | Frekvens | Kumulativ frekvens |
|---|---|---|
Mer om:
Denne oppgaven er om Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer. Se frekvenstabell Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere. Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien. Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Frekvens
Kumulativ frekvens

Statistikk
For flere eksempler og forklaringer se artikkelen Frekvens.
Oppgave 2 (1 poeng) Nettkode: E-4BV2
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker:
Et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
En god strategi er å skrive hvert
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Svar: .
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall. Eksempel: Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerStandardform
Mer om tall på standardform finner du i artikkelen Tall på standardform. For flere eksempler og forklaringer om potensregler se artikkelen Rask gjennomgang av regneregler for potens og røtter.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleieren.
Oppgave 3 (2 poeng) Nettkode: E-4BV4
Hvilken av de to brøkene A og B nedenfor har størst verdi?
A:
B:
Løsningsforslag
Jeg tenker:
Vi skal regne med
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Vi prøver å få tallene på samme form, og starter med . Vi vil gjerne ha bort brøkstreken, og det gjør vi ved å “flytte opp” nevneren og bytte fortegn på eksponenten. Det gjør vi ved å multiplisere med over og under brøkstreken. Vi fårDet kan også være lurt å
Primtallsfaktorisering
Er å skrive et tall som et produkt av primtall.
Eksempel:
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Vi fortsetter med . Først ser vi at siden , så er Videre er , og da er . Her bruker vi potensregelen med et produkt som grunntall. Eksponenten dukker opp på hver faktor når vi løser opp parentesen. Dermed får vi Dette er altså nevneren i brøken , så er lik Vi multipliserer brøken med over og under brøkstreken for å få et penere svar. Da får vi
Nå kan vi sammenligne og . Brøken kunne skrives som . Vi kan få dette mer likt ved å skrive det som en brøk; vi vet nemlig at . Dermed er lik , og er lik . Fra dette ser vi at er større enn , siden .
Svar: , så er størst
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En potens består av et grunntall og en eksponent. Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent. En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten. Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde.Potens
Eksempel: Grunntall
Eksponent
xn = x · x · x...· x, n gangerBrøk

For flere eksempler og forklaringer se artikkelen Inger Christin forteller om potensregler.
For å øve mer, se oppgavesettet om potenser i Treningsleieren.
Oppgave 4 (5 poeng) Nettkode: E-4BV7
Sigvald får følgende tilbud fra foreldrene sine:
|
TILBUD 1 Du får 100 kroner i fast |
TILBUD 2 Du får 50 kroner i fast |
a)
Sett opp et matematisk uttrykk som kan være en modell for tilbud 1, og et matematisk uttrykk som kan være en modell for tilbud 2.
Løsningsforslag a)
Jeg tenker:
Vi kan sette opp funksjonene og tilhørende henholdsvis tilbud og tilbud slik at er antall kroner i ukelønn hvis Sigvald vasker opp ganger, og tilsvarende for .
Vi lar være antall kroner Sigvald får i ukelønn hvis han vasker opp ganger og godtok tilbud , og at er tilsvarende for tilbud . La oss starte med å finne et uttrykk som beskriver tilbud . Vi ser at er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
På helt tilsvarende vis finner vi at stigningstallet til er , og at konstantleddet er . Dermed kan vi modellere tilbud med
Svar: Vi kan modellere tilbud med , og tilbud med .
Mer om:
Denne oppgaven er om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleieren.
b)
Skisser grafen til hver av modellene, og gi Sigvald råd om hvilket tilbud han bør velge.
Løsningsforslag b)
Jeg tenker:
Vi har
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi merker oss at det står at vi skal skissere grafen, og da trenger vi ikke ta med alle detaljene vi skulle ha tatt med hvis det hadde stått “tegn grafen”. Vi starter med . Det første vi gjør er å lage et
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.

Vi vet at er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.

Vi kan gjøre det samme med . Fra konstantleddet får vi at er et punkt på grafen, og hvis Sigvald vasker opp ganger får han en ukelønn på kroner, så er et annet punkt på grafen. Vi tegner den rette linjen mellom de to punktene. Vi gjør det i samme koordinatsystem som tidligere, slik at vi kan sammenligne de to modellene.
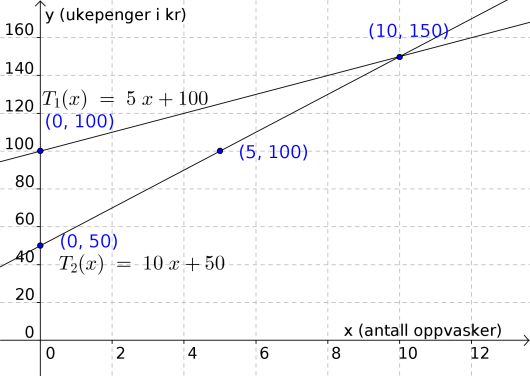
Her ser vi at gir mest ukelønn når , og at gir mest ukelønn når . Dermed burde Sigvald godta tilbud hvis han vasker opp mindre enn ganger per uke, og godta tilbud hvis han vasker opp mer.
Svar: Sigvald burde godta tilbud 1 hvis han vasker opp mindre enn 10 ganger per uke, og godta tilbud 2 hvis han vasker opp mer.

Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Graf
Skjæringspunkt

Koordinatsystem

Stigningstall

For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleierene.
Oppgave 5 (2 poeng) Nettkode: E-4BWN
Tegn av tabellen nedenfor i besvarelsen din, gjør beregninger, og fyll inn det som mangler.
| Plassverdisystem med grunntall 10 |
Plassverdisystem med grunntall 2 |
Løsningsforslag
Jeg tenker:
(NB! Omforming til og fra binære tall er ikke lenger med i læreplanen for 2P.) Vi skal finne ut hva er i titallsystemet, og hva er i totallsystemet.
Vi starter med å finne ut hva er i totallsystemet. Dette tallet skal stå i første rute. Tallet er likVi vet at , , , , og . Da blir regnestykket over likVi fyller inn dette i tabellen.
| Plassverdisystem med grunntall 10 | Plassverdisystem med grunntall 2 |
|---|---|
Videre skal vi finne ut av hva er i totallsystemet. Det gjør vi ved å finne ut hvilke toerpotenser man skal legge sammen for å få . Vi har , og det er den største toerpotensen som er under . Videre har vi , og den største toerpotensen som er under er . Til slutt er . Da ser vi atDet betyr at vi kan skrive somDermed er det samme som i totallsystemet. Vi fyller inn dette i tabellen, og den ferdige tabellen er vist under.
Svar:
| Plassverdisystem med grunntall 10 | Plassverdisystem med grunntall 2 |
|---|---|
Mer om:
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Tabell

Potens
Eksempel:
For flere eksempler og forklaringer se artikkelen 2-tallsystem (binært system).
Visste du at:
Måten man skriver desimaltall på, er ikke entydig. Et slående eksempel er at er det samme som tallet (uendelig nitall). Et enkelt bevis for dette går slik:
Men er ikke det eneste eksempelet. Tallet kan skrives som , og kan skrives som . Faktisk er de eneste tallene med entydig desimalutvikling (som det heter), tall som ikke kan skrives med et endelig antall desimaler. Eksempler er og . Dette er brøker med andre tall enn og i nevneren, som er primtallsfaktorene til . Dette kan generaliseres til andre tallsystemer også: I -tallsystemet kan brøker som bare har primtallsfaktorene til i nevneren, skrives på flere måter på desimalform. For eksempel kan brøken skrives både som og som i totallsystemet, fordi er en (den eneste) primtallsfaktoren i .
Oppgave 6 (3 poeng) Nettkode: E-4BXC
Stian har kjøpt en bruktbil. Bilen kostet 100 000 kroner.
Anta at verdien vil avta med 10 % per år.
a)
Sett opp en modell som Stian kan bruke for å regne ut verdien av bilen i årene som kommer.
Løsningsforslag a)
Jeg tenker:
Hvis en verdi avtar med per tidsenhet, så er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Bilen vil være verdt etter år.
Mer om:
Denne oppgaven er om
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
For flere eksempler og forklaringer se artikkelen Hva er prosent?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
b)
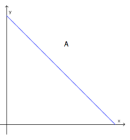
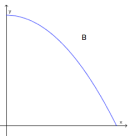
Hvilken av grafene nedenfor er grafen til ? Begrunn svaret ditt.
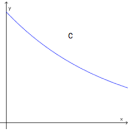
Løsningsforslag b)
Jeg tenker:
Verdien til bilen vil avta mest i begynnelsen, og deretter slake ut.
Verdien til bilen vil avta forholdsvis raskt i begynnelsen, men deretter flate ut, fordi av er mer enn av et mindre tall, for eksempel . En måte å se på det på, er at etter hvert år så skal verdien kuttes med én tiendedel. Da ser vi at er den eneste grafen som passer. Grafen er dessuten den eneste som ikke blir 0. Det stemmer med modellen vår, for det finnes ikke noen verdi slik at .
Svar: Grafen er riktig, fordi verdien avtar mer i begynnelsen enn etter hvert. Det kan også argumenteres med at er den eneste grafen som ikke treffer -aksen, akkurat som .
Mer om:
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Den horisontale aksen i et koordinatsystem. Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Graf
x-akse

Kalles også førsteakse.Prosent
Eksponentialfunksjon

For flere eksempler og forklaringer se artikkelen Typer av funksjoner og Eksponentiallikninger.
For å øve mer, se oppgavesettet om eksponentialfunksjoner i Treningsleieren.
Oppgave 7 (2 poeng) Nettkode: E-4BXG
Tabellen nedenfor viser inntektene til personene i et borettslag.
| Inntekt (i 1000 kroner) |
Antall |
Bestem gjennomsnittsinntekten til personene i borettslaget.
Løsningsforslag
Jeg tenker:
Dette er klassedelt materiale, og da antar vi at
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Det er personer i klassen . Vi antar at disse er jevnt fordelt utover klassen, slik at gjennomsnittlig inntekt av disse er (tusen kroner). Når vi skal regne ut
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Vi kunne ha regnet ut brøken for hånd, men det kan være enklere å bruke det faktum at på
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Svar: , gitt at dataene er jevnt fordelt innenfor hver klasse.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
Oppgave 8 (4 poeng) Nettkode: E-4BXJ
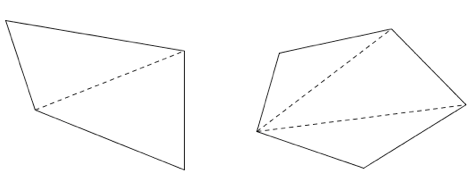
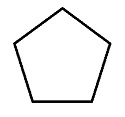
Vinkelsummen i en trekant er .
a)
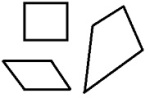
Bruk figurene ovenfor til å bestemme vinkelsummen i en firkant og i en femkant.
Løsningsforslag a)
Jeg tenker:
Firkanter og femkanter kan deles opp i trekanter som vist på tegningene.
Vi kan bruke
Vinkelsum
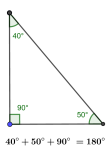
Summen av alle vinklene i en mangekant.
Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.
Vi tegner opp en hjelpetegning.
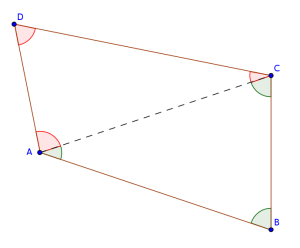
Ut i fra tegningen kan vi se at vinkelsummen til firkanten bare er summen av vinkelsummene i de to trekantene:Dette blir altså lik . Vi kan være mer pedantiske og finne vinkelsummen med regning. Vinkelsummen i firkanten erVi ser at , og at . Dette kan vi sette inn i vinkelsummen over, og vi fårNå kan vi gjøre om på rekkefølgen av leddene over.Men uttrykket i den første parentesen over er vinkelsummen i , og det andre uttrykket er vinkelsummen i , så vinkelsummen i firkanten er . Vi merker oss at alle firkanter kan deles inn i to trekanter på denne måten, så vinkelsummen i enhver firkant er .
Vi kan gjøre det samme for femkanten. Femkanter kan deles inn i tre trekanter, og da blir vinkelsummen i femkanten lik .
Svar: Vinkelsummen i en firkant er , og vinkelsummen i en femkant er .
Mer om:
Denne oppgaven er om Femkant er en geometrisk figur med fem sidekanter. En firkant er en geometrisk figur med fire hjørner og fire sidekanter. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Summen av alle vinklene i en mangekant. Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader. Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.Femkant
Firkant
Trekant

Vinkelsum

Geometri
For flere eksempler og forklaringer se artikkelen Vinkelsum i en mangekant.
b)
Bestem vinkelsummen i en sekskant og i en åttekant.
Løsningsforslag b)
Jeg tenker:
Vi kan dele inn de nye figurene inn i
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
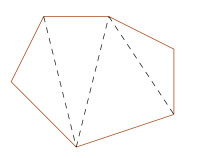
Vi kan dele inn sekskanter og åttekanter slik som i forrige oppgave. En sekskant kan deles inn i trekanter:
Mens en åttekant kan deles inn i :
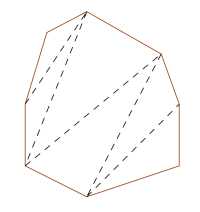
Dermed er vinkelsummen i en sekskant lik , mens vinkelsummen i en åttekant er .
Svar: Vinkelsummen i en sekskant , og vinkelsummen i en åttekant er lik .
Mer om:
Denne oppgaven er om Femkant er en geometrisk figur med fem sidekanter. En firkant er en geometrisk figur med fire hjørner og fire sidekanter. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Summen av alle vinklene i en mangekant. Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader. Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.Femkant

Firkant

Trekant

Vinkelsum

Geometri
For flere eksempler og forklaringer se artikkelen Tom forteller om vinkler og vinkelmål.
c)
Trekanter, firkanter, femkanter og så videre kalles mangekanter.
I en mangekant er vinkelsummen . Hvor mange kanter har denne mangekanten?
Løsningsforslag c)
Jeg tenker:
Vi kan prøve å finne et system ut i fra deloppgavene a) og b).
Vi kan løse denne oppgaven på to måter; den første går ut på å prøve seg frem, mens den siste går ut på å lage en generell formel for vinkelsummen i en -kant.
Vi kan få en firkant fra en trekant ved å “lime på” en trekant til en av sidene, slik som vist i a). Tilsvarende kan vi en femkant ved å “lime på” en trekant til en firkant. Hver gang vi limer på en trekant, adderer vi til vinkelsummen av mangekanten. En åttekant hadde vinkelsum . Legger vi til en trekant, slik at vi får en nikant, blir vinkelsummen . Legger vi på en trekant til blir vinkelsummen ; legger vi på enda en blir vinkelsummen , og legger vi på en siste trekant blir vinkelsummen , og det var det som var etterspurt. Vi har lagt til kanter på en åttekant, så figuren med vinkelsum er en tolvkant.
Vi kan generalisere dette. I en trekant er vinkelsummen . Legger vi på trekanter, så får vi en -kant, og denne har vinkelsum . Dette passer med at firkanter har vinkelsum , at åttekanter har vinkelsum , og så videre. Dermed er vi ute etter det tallet som gir en vinkelsum på . Vi ser at vi kan multiplisere med for å få ; dermed er så . Derfor har mangekanten kanter.
Svar: kanter.
Mer om:
Denne oppgaven er om En mangekant er en geometrisk lukket figur som er satt sammen av rette linjestykker. Kalles også en polygon. Eksempel: trekant, firkant, femkant (pentagon) og sekskant (heksagon). En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. Summen av alle vinklene i en mangekant. Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader. Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.Mangekant
Trekant

Vinkelsum

Geometri
For flere eksempler og forklaringer se artikkelen Vinkelsum i en mangekant.
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4BXO
| Stortinget ved starten av perioden 2009-2013 |
|
| Parti | Antall representanter |
| Arbeiderparti | 64 |
| Fremskrittspartiet | 41 |
| Høyre | 30 |
| Sosialistisk Venstreparti | 11 |
| Senterpartiet | 11 |
| Kristelig Folkeparti | 10 |
| Venstre | 2 |
a)
Lag et sektordiagram som illustrerer opplysningene gitt i tabellen ovenfor.
Løsningsforslag a)
Jeg tenker:
Vi kan bruke et program for regneark.
Vi velger Excel. Det første vi gjør er å legge inn tabellen i regnearket.
Vi vil lage et sektordiagram. Derfor markerer vi tabellen vi har lagt inn, trykker “Sett inn”, og velger sektordiagram.
Resultatet er vist under.
Svar: 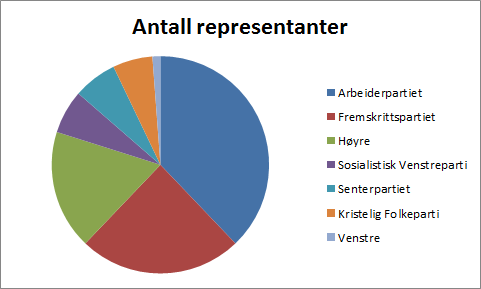
Mer om:
Denne oppgaven er om regneark,
Sektordiagram
Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Lynkurset om regneark er under utarbeidelse og kommer snart.
For å øve mer, se opppgavesettet om sektordiagram i Treningsleieren.
b)
| Stortinget ved starten av perioden 2009-2013 |
||
| Parti | Antall kvinner | Antall menn |
| Arbeiderparti | 32 | 32 |
| Fremskrittspartiet | 10 | 31 |
| Høyre | 9 | 21 |
| Sosialistisk Venstreparti | 3 | 8 |
| Senterpartiet | 7 | 4 |
| Kristelig Folkeparti | 4 | 6 |
| Venstre | 2 | 0 |
Lag et passende diagram som illustrerer opplysningene gitt i tabellen ovenfor.
Løsningsforslag b)
Jeg tenker:
Vi kan bruke regneark. Et
Stolpediagram
Et søylediagram uten bredde på søylene.
Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak.
Se Søylediagram
Vi bruker Excel. Det første vi gjør er som vanlig å legge inn tabellen i regnearket.
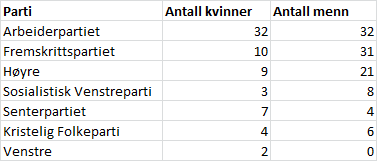
Vi markerer tabellen, og trykker “Sett inn” for å finne et passende diagram. Vi velger et gruppert stolpediagram, for da er det lett å se hvor mange kvinner og menn som har stemt på de diverse partiene. Resultatet er vist under.
Svar: 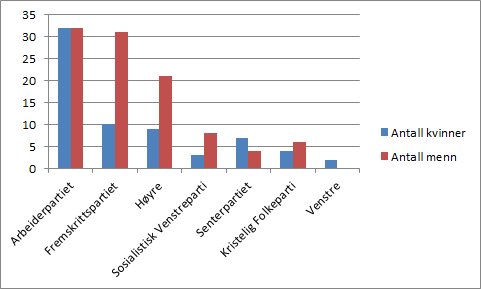
Mer om:
Denne oppgaven er om regneark, Et søylediagram uten bredde på søylene. Søyle- og stolpediagram brukes ofte om hverandre, og forskjellen er bare en definisjonssak. Se Søylediagram Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Stolpediagram
Statistikk
For flere eksempler og forklaringer se artikkelen Søyle- og stolpediagram i lynkurset Statistikk (del II). Lynkurset om regneark er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om søylediagram i Treningsleieren.
Oppgave 2 (6 poeng) Nettkode: E-4BXT
Familien din er på ferie og skal leie en bil. Tabellen nedenfor viser hvor mye det koster å leie bilen hvis dere kjører 100 km, og hvor mye det koster hvis dere kjører 150 km.
| Antall kilometer | 100 | 150 |
| Pris (kroner) | 500 | 625 |
Det er en lineær sammenheng mellom antall kilometer og pris.
a)
Hva vil det koste å leie bilen dersom dere skal kjøre 300 km?
Løsningsforslag a)
Jeg tenker:
Siden det er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Det koster å kjøre , og for å kjøre . Det betyr at det koster ekstra per kilometer man kjører. Hvis vi skal kjøre bilen i , så må vi legge til til prisen det koster å kjøre . Dermed har vi pris for er lik
.
Svar:.
Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen .Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
b)
Dersom dere kjører km, må dere betale kroner.
Bestem en modell på formen som viser sammenhengen mellom og .
Løsningsforslag b)
Jeg tenker:
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi finner den lineære (rette) modellen i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

Her ser vi at likningen til modellen vår er .
Alternativ løsning
Vi kan også finne denne likningen ved regning. Det koster ekstra å kjøre ; per kilometer blir dette . Det betyr at når øker med én i uttrykket , så øker med . Derfor er
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Svar: .
Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer se artikkelen Førstegradslikninger. For mer om lineære funksjoner se artiklene Fra en funksjon til en graf og Fra en graf til en funksjon i lynkurset Funksjoner (del I).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
c)
Gi en praktisk tolkning av tallene og i denne oppgaven.
Løsningsforslag c)
Jeg tenker:
Tallet er
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Vi vet at hvis man reiser kilometer, så må man betale kroner. Hvis vi reiser i , så må vi betale kroner. Det betyr at det koster å leie bilen i utgangspunktet, så startprisen er . Videre koster det per kilometer vi kjører.
Svar: Tallet er hvor mye det koster å leie bilen i utgangspunktet, og er antall kroner det koster å kjøre per kilometer.
Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen . Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen. Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Stigningstall

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Hvorfor ser grafen ut som den gjør?.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Oppgave 3 (3 poeng) Nettkode: E-4BXX
Petter vil sende en e-post med en matematikkoppgave til to personer 1. januar. Anta at hver av de to personene sender e-posten videre til to nye personer dagen etter, at hver av de fire som da får den, også sender den videre til to nye personer dagen etter at de mottok den, og at e-posten fortsetter å spres på samme måte i dagene framover.
a)
Hvor mange personer vil motta e-posten 6. januar?
Løsningsforslag a)
Jeg tenker:
Antall personer som sender e-posten dobles hver dag.
. januar sendes (og mottas) det e-poster. . januar sender hver av disse e-poster hver, og så da mottas det e-poster. Den . januar sender hver av disse e-poster, så det mottas e-poster. Hver dag dobles altså antall e-poster mottatt. Den . januar mottas det e-poster, den . januar mottas det e-poster, og den 6. januar mottas det e-poster. Generelt mottas det e-poster etter dager.
Svar: e-poster
Mer om:
Denne oppgaven er om En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.Potens
Eksempel:
For flere eksempler og forklaringer se artikkelen Potenser med samme grunntall.
For å øve mer, se oppgavesettet om potensregning i Treningsleieren.
b)
På hvilken dato vil antall mottatte e-poster på én dag for første gang bli større enn én milliard?
Løsningsforslag b)
Jeg tenker:
Fra deloppgave a) vet vi at det mottas e-poster etter dager. Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi vil finne ut hvor stor må være for at skal være større enn én milliard (). Det kan vi gjøre ved å prøve å sette inn større og større tall for , eller så kan vi løse problemet grafisk. Vi finner ved prøving og feiling at
så første dag med mer enn én milliard mottatte e-poster er 30. januar.
Alternativ løsning
Vi tegner
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
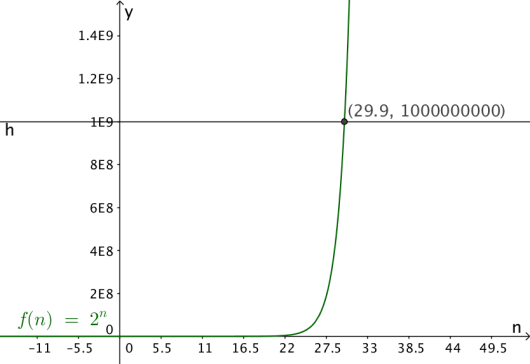
Her ser vi at , altså at . Det betyr at det mottas 1 milliard e-poster den 30. januar.
Svar: Den 30. januar.
Mer om:
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Skjæringspunkt

Linje
Potens
Eksempel: Funksjon
For flere eksempler og forklaringer om skjæringspunkter se artikkelen Grafisk løsning av likninger og mer om potensregning i artikkelen Oppsummering av regneregler for potenser.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
Visste du at:
Denne oppgaven viser hvor utrolig stort eksponentiell vekst kan være. Her er også forklaringen for hvorfor kjedebrev når veldig mange.
Oppgave 4 (7 poeng) Nettkode: E-4BY5
Tabellene nedenfor viser resultatene for de åtte beste utøverne på 1500 m skøyter for menn under OL i 1968 og under OL i 2010.
OL 1968
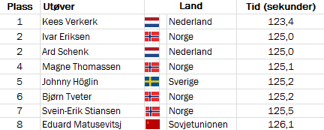
OL 2010
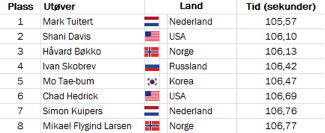
a)
Hvor mange prosent sank vinnertiden med fra 1968 til 2010?
Løsningsforslag a)
Jeg tenker:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Vi vil finne ut hvor mange prosent vinnertiden sank med fra til . Hvis er
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
Svar: Cirka .
Mer om:
Denne oppgaven er om Prosent betyr hundredel og skrives %. Eksempel: Hvor mange prosent er 1 av 4? . Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi. Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.Prosent
Vekstfaktor
For flere eksempler og forklaringer se artikkelen Prosent av hva da?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.
b)
Bestem gjennomsnittstiden for de åtte beste i 1968 og for de åtte beste i 2010.
Løsningsforslag b)
Jeg tenker:
Vi skal finne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Hvis vi skulle ha regnet ut
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
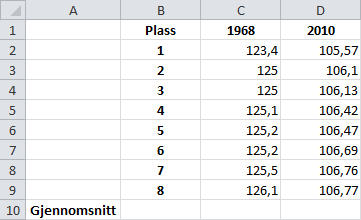
Vi kan finne gjennomsnittene på to måter. Enten kan vi gjøre det manuelt, ved å summere opp tallene i hver kolonne og dividere med . For gjør vi dette ved å skrive
=SUMMER(C2:C9)/8(C2:C9 refererer til rutene C2, C3, ..., C9, og det er i disse rutene tidene ligger i.) Vi kan også bruke Excels innebygde funksjoner, ved å skrive
=GJENNOMSNITT(C2:C9)Uavhengig av hvilken metode vi bruker, får vi at gjennomsnittet i var cirka sekunder, mens gjennomsnittet i var cirka sekunder. Vi bruker samme antall desimaler som dataene som er oppgitt.
Svar: Gjennomsnittet i var cirka sekunder, og gjennomsnittet i var cirka sekunder.
Mer om:
Denne oppgaven er om Gjennomsnitt er en middelverdi av alle dataene. Gjennomsnittet finner du ved å: Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Gjennomsnitt
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4. Statistikk
For flere eksempler og forklaringer se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleieren.
c)
Bestem standardavviket for de to tallmaterialene.
Hvorfor er standardavviket større i 1968 enn i 2010?
Løsningsforslag c)
Jeg tenker:
Vi skal finne
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Vi bruker samme regneark som i forrige oppgave. Vi bruker Excels innebygde funksjon for å finne
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
=STDAV.P(C2:C9)Vi bruker STDAV.P fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt STDAV, ville vi fått estimerte verdier basert på utvalg.
Det er det samme med , bare at vi bytter ut med . Da får vi følgende regneark.
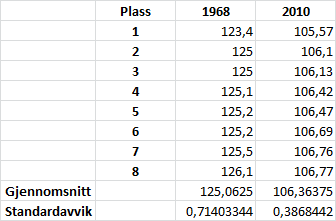
Standardavviket til tidene i var cirka , og standardavviket for var cirka . Vi ser at tidene i ligger mellom til sekunder, mens tidene i ligger mellom og , altså et betydelig mindre intervall. Vi ser dermed at tidene i varierer mer enn tidene i , og det er akkurat derfor standardavviket er størst i .
Svar: Standardavviket til tidene i var cirka sekunder, og standardavviket for var cirka sekunder. Standardavviket i er større enn i fordi de åtte beste tidene varierte mer i enn i .
Mer om:
Denne oppgaven er om Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet. Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.Standardavvik
Statistikk
For flere eksempler og forklaringer se artikkelen Varians og standardavvik.
Oppgave 5 (8 poeng) Nettkode: E-4BYC

Tabellen nedenfor viser sammenhengen mellom diameteren til en dorull og hvor mange meter papir som er brukt av dorullen.
| Antall meter papir som er brukt av dorullen |
0 | 2 | 6 | 10 | 12 |
| Dorullens diameter (millimeter) |
102 | 96 | 83 | 72 | 67 |
a)
Tegn et koordinatsystem med meter som enhet langs -aksen og millimeter som enhet langs - aksen. Marker verdiene fra tabellen ovenfor som punkter i koordinatsystemet.
Løsningsforslag a)
Jeg tenker:
Vi kan bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Først skriver vi inn alle punktene i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Svar: 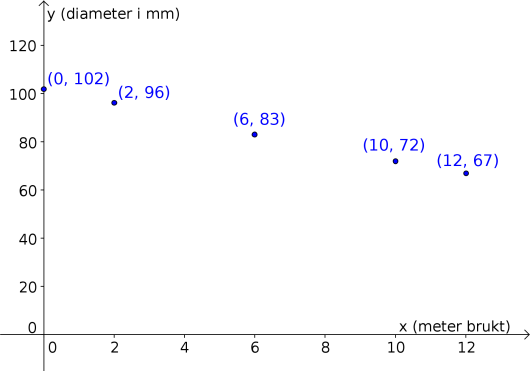
Mer om:
Denne oppgaven er om Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0). En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirennKoordinatsystem

Graf
Tabell

For flere eksempler og forklaringer se artikkelen Å lage en matematisk modell. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleieren.
b)
Bruk regresjon til å bestemme en lineær funksjon som passer godt med punktene fra oppgave 5 a). Tegn grafen til funksjonen i samme koordinatsystem som du brukte i oppgave 5 a).
Løsningsforslag b)
Jeg tenker:
Vi bruker
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Vi kan finne den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
RegLin[A, B, C, D, E]i “Skriv inn”-feltet i GeoGebra. Resultatet er vist under. Vi høyreklikker på linjen i algebrafeltet, og velger “Likning ” for å få ligningen til linjen på den kjente formen. Vi ser at linjen har ligningen .
Svar: Linjen har likningen .

Mer om:
Denne oppgaven er om En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. Lineære funksjoner er funksjoner som er skrevet på formen . Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Ligning
Regresjon
Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Regresjon 1.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleieren.
c)
En tom dorull har en diameter på 38 mm.
Hvor mange meter papir er det på en ny dorull ifølge modellen i oppgave 5 b)?
Løsningsforslag c)
Jeg tenker:
Dorullen er tom når diameteren er på millimeter. Vi lurer på hvor mange meter dopapir som er brukt når dorullen har denne diameteren.
Vi er ute etter å finne hvor mange meter dopapir som er brukt når diameteren til dorullen er . Det gjør vi ved å finne ut når den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
y = 38i “Skriv inn”-linjen i den samme
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Vi ser at skjæringspunktet har koordinater . Det tolkes slik: Når vi har brukt meter dopapir, så er diameteren til dorullen millimeter, altså er dorullen tom. Det må bety at det er meter dopapir på dorullen når den er ny.
Svar: meter
Mer om:
Denne oppgaven er om Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen. Lineære funksjoner er funksjoner som er skrevet på formen . En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Skjæringspunkt

Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Linje
Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleieren.
d)
På pakken med doruller står det at hver dorull inneholder 160 ark. Hvert ark er 14 cm langt.
Hvordan stemmer modellen i oppgave 5 b) med dette?
Løsningsforslag d)
Jeg tenker:
Vi må finne ut hvor mange meter dopapir det er på rullen i følge pakken, og sammenligne med svaret vi fant i forrige oppgave.
Hvis hvert ark er langt og hver dorull har ark, så må det være dopapir på hver dorull. I følge modellen vår er det meter, så vi var ikke så langt unna.
Svar: I følge pakken er det dopapir per rull, og i følge modellen vår er det . Det er en akseptabel feilmargin.
Mer om:
Denne oppgaven er om Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Hva er matematisk modellering?.
Oppgave 6 (6 poeng) Nettkode: E-4C0R
| Bilmerke | Volvo | |
| Bilmodell | V50 | |
| Nybilpris i 2006 | 299 990 | |
| Antatt verdi i 2011 | 171 000 | |
| Verditap | 128 900 | |
| Verditap årlig | 25 780 |
I 2011 kjøpte Helene en bruktbil. Hun fant da tabellen ovenfor på Internett. Alle beløp er oppgitt i kroner.
a)
Forklar at det årlige verditapet på bilen er beregnet ved hjelp av en lineær modell, og bestem denne modellen.
Løsningsforslag a)
Jeg tenker:
Verditapet er en konstant sum per år. Det er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Bilen var verdt i utgangspunktet, og i følge tabellen mistet den i verdi årlig. Det betyr at etter ett år, så var bilen verdt ; etter to år var bilen verdt , og så videre. Etter år var bilen dermed verdt Hvis er bilens verdi i kroner etter år, så er altså Dette er modellen som er brukt i tabellen, og det er på formen , så modellen er lineær.
Svar: Hvis er bilens verdi i kroner etter år, så er (i følge tabellens modell). Dette funksjonsuttrykket er på formen , så modellen er lineær.
Mer om:
Denne oppgaven er om Tabeller brukes til å organisere informasjon, ofte i kolonner og rader. Eksempel: rutetabell for buss, resultatliste for skirenn Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner er funksjoner som er skrevet på formen .Tabell

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
b)
Helene lurer på om det vil være mer realistisk å bruke en eksponentiell modell.
Bestem en eksponentiell modell som totalt gir samme verditap på bilen fra 2006 til 2011 som den lineære modellen.
Løsningsforslag b)
Jeg tenker:
Vi kan finne en
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi bruker
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
P(x) = RegEksp[A, B]i “Skriv inn”-vinduet i GeoGebra.

Vi ser at den eksponentielle modellen har funksjonsuttrykk .
Svar: Hvis er verdien til bilen år etter , så er .
Mer om:
Denne oppgaven er om Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet. En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Regresjon
Potens
Eksempel: Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Johannes viser eksponential- og logaritmefunksjoner og lynkurset Kultur og modellering.
For å øve mer, se oppgavesettet funksjoner i praktiske situasjoner i Treningsleieren.
c)
Hva er Helenes bil verd i 2013 ifølge den lineære modellen?
Hva er Helenes bil verd i 2013 ifølge den eksponentielle modellen?
Løsningsforslag c)
Jeg tenker:
Vi bruker den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Svar: I følge den lineære modellen vil bilen være verdt , og i følge den eksponentielle modellen vil den være verdt .
Mer om:
Denne oppgaven er om Lineære funksjoner er funksjoner som er skrevet på formen . En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Matematiske modeller brukes ofte for å beskrive fenomener i naturen. Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på. Lineære funksjoner

Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.Eksponentialfunksjon

Matematisk modell
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere eksempler og forklaringer se artikkelen Hva er matematisk modellering?.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleieren.




