Øvingsoppgaver med fasit

I $\mathrm{\Delta }PQR$ er $\angle$R = 27,2°, PR = 23,1 cm og QR = 8,2 cm. Regn ut arealet av trekanten.

I $\boxed{\text{?}}ABCD$ er AB = 6,0 cm, AD = 4,0 cm, DC=5,2 cm, $\angle A={90}^o$ og $\angle D={105}^o$.

Regn ut arealet av firkanten.

I en figur ABCD er AB og CD parallelle (AB || CD)

AB=BC=5 cm, CD = 7cm, og korteste avstand mellom AB og CD er 3 cm.

a)      Konstruer figuren.

b)      Hva heter figuren?

c)      Regn ut areal og omkrets.

 Et rektangel har sider AB = CD = 12 cm og BC = DA = 5 cm. Konstruer rektangelet. Avsett E på AB slik at AE = 7 cm. Merk av punktet F, som ligger i rektangelet, 4 cm fra DA og samtidig 2 cm fra AB. Regn ut omkrets og areal av femkanten AECFD(A).

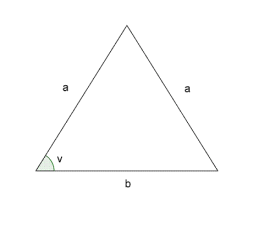
a) Bruk arealformelen $A=\frac{g\cdot h}{2}$ til å vise at arealet av trekanten er $A=\frac{b\sqrt{a^2-\frac{b^2}{4}}}{2}$.

b) Vis at $\sin v=\frac{\sqrt{a^2-\frac{b^2}{4}}}{a}$.

c) Vis at arealet av trekanten også er gitt ved $A=\frac{1}{2}a\cdot b\cdot \sin v$.

a) Konstruer en likesidet trekant ABC med sider 5 cm.

b) Roter trekanten 60 grader mot urviseren om B.

c) Hva heter den figuren du nå har fått?

d) Kall det siste hjørnet i den nye figuren for E og speil trekanten AEB om EB.

e) Hva heter den figuren du nå har fått?

f) Kall det siste hjørnet i den nye figuren for F og regn ut areal og omkrets av AEFC.

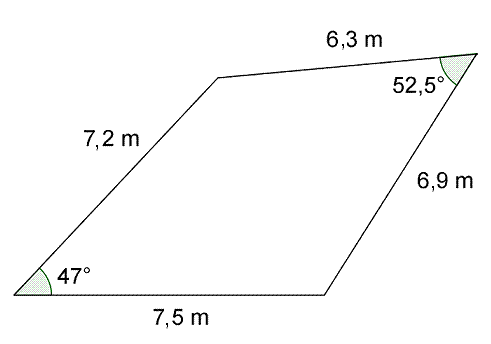
Hva er arealet av firkanten?

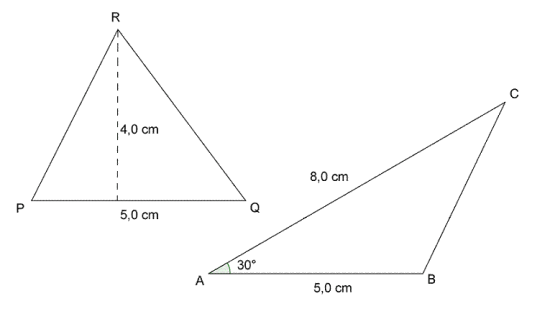
Hvilken av trekantene har størst areal?

Firkanten $ABCD$ er et parallellogram. $AB=a$ og $AD=b$, mens vinkelen mellom $AB$ og $AD$, kalles $v$. Finn et uttrykk for arealet av parallellogrammet.

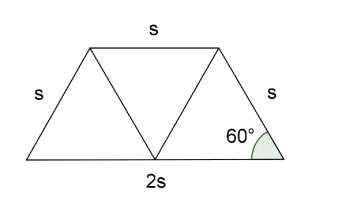
Tre likesidete trekanter med sidelengde $s$ settes sammen til å danne et trapes.

a) Tegn trapeset og vis at omkretsen blir $5s$.

b) Bruk én av trekantene til å vise at $\sin \left({60}^o\right)=\frac{\sqrt{s^2-\frac{s^2}{4}}}{s}=\frac{\sqrt{3}}{2}$.

c) Vis at arealet av trapeset er $A=\frac{3\sqrt{3}}{4}{s}^2$.