Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Funksjonen f er gitt ved
a) Tegn grafen til f.
b) Finn bunnpunktet til f.
2
3
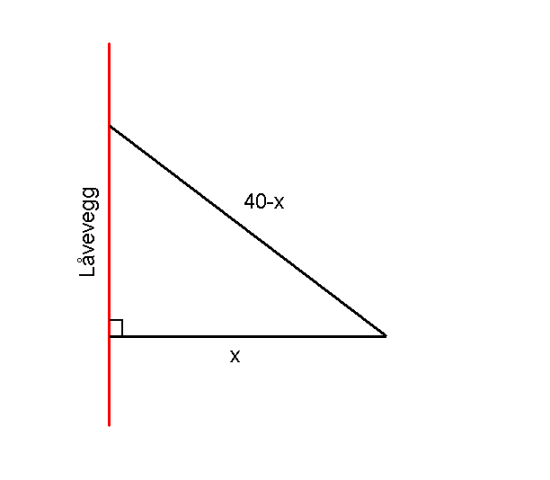
En bonde har m netting-gjerde og skal lage en innhegning for noen høns. Han bestemmer seg for å bruke låveveggen som den ene siden av innhegningen. På grunn av vanskelige grunnforhold med mye stein, ønsker han å bruke bare én påle, og dra nettingen rundt denne. Nettingen skal festes i veggen på to steder, og på det ene stedet, må gjerdet danne vinkel med låveveggen, se figur.
a) Vis at arealet av innhegningen er gitt ved .
b) Finn største mulige areal grafisk på lommeregneren.
4
5
Tegn grafen på lommeregneren og finn koordinatene til eventuelle topp- og bunnpunkter for disse funksjonene:
6
Den deriverte til en funksjon er gitt ved .
a) Vis at .
b) Bestem nullpunktene til .
c) Bestem i hvilke intervaller vokser og avtar.
7
8
9
f(x)
10
Tegn grafen ved hjelp av et digitalt verktøy og finn koordinatene til eventuelle topp- og bunnpunkter for følgende funksjon:
Fasit
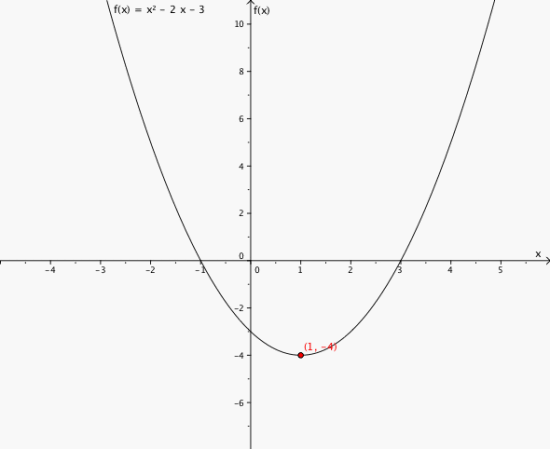
1
a)
Grafen til f(x) og bunnpunktet (1,-4)
b) Bunnpunkt (1,4)
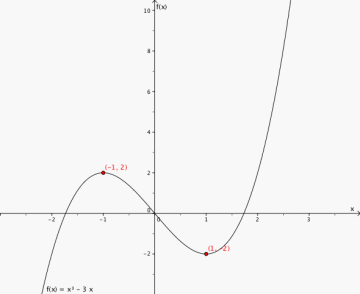
2
Toppunkt (-1,2)
Bunnpunkt (1,-2)
Grafen stiger når x<-1 og når x>1. Grafen synker når -1
3
b)
4
5
Toppunkt: (-0,33, 1,19)
Bunnpunkt: (1, 0)
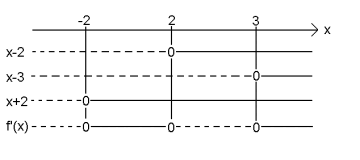
6
b)
c)
avtar i og i .
vokser i og i .
7
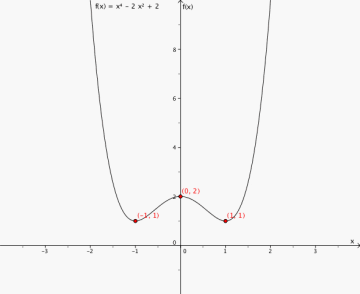
toppunkt (0,2)
bunnpunkter (-1,1) og (1,1)
Grafen synker når x<-1 og når 0
8
9
10
toppunkt:
bunnpunkt: