Øvingsoppgaver med fasit

Lenke til dette oppgavesettet (kan bokmerkes)

Oppgaver

1

ID: 34592

Finn den deriverte til følgende tredjegradsfunksjon:

$f (x) = \frac{7}{5} x^{3} - \frac{1}{3} x^{2} - \frac{19}{3} x + \frac{1}{2}$

2

ID: 33555

Finn et uttrykk for den deriverte til f.

$f (x) = - \frac{1}{3} x^{2} + \frac{2}{5} x + 1000$

3

ID: 49711

Det er i dag 250 arbeidsledige i en kommune. Om $x$ år forventes antall arbeidsledige å være gitt ved funksjonen

$A (x) = - 2 x^{3} + 12 x^{2} - 6 x + 250$ .

Prognosen er imidlertid kun gyldig for de neste seks årene, dvs. $x \in [0, 6]$ .

a) Tegn grafen på lommeregneren og beskriv utviklingen i antall arbeidsledige med ord.

b) Hva er det høyeste antallet arbeidsledige som forventes i kommunen? Løs grafisk og ved regning.

c) Når er forventet antall arbeidsledige lik 270? Løs grafisk.

d) Hva er den forventede prosentvise endringen for hele seksårsperioden?

4

ID: 83848

Deriver $p (t) = {\frac{1}{4} t}^{4} + \frac{1}{2} t^{2} + \frac{1}{2}$ . Deriver den deriverte.

5

ID: 49698

La $f$ være funksjonen $f (x) = x^{3} - 4 x + 5$ .

a) Finn likningen til tangenten for $x = 0$ .

b) Finn likningen til tangenten for $x = 2$ .

c) Har grafen til $f$ tangenter som er parallelle med tangentene i a) og b)? Undersøk dette og finn evt. likningene til de parallelle tangentene.

6

ID: 83760

Kan to forskjellige potensfunksjoner har samme derivert? Begrunn svaret.

7

ID: 35644

Formelen

h (t) = - \frac{1}{30} t^{3} + \frac{5}{2} t^{2}, t \in [0, 50]

gir oss høyden av et tre målt i centimeter t år etter at frøet spirte.

a) Finn høyden av treet om 20 år og 40 år.

b) Finn den deriverte av h

c) Regn ut veksthastigheten om 20 år og om 40 år

8

ID: 35602

Finn

f^{'} (x)

når f er funksjonen gitt ved

f (x) = - 3 x + 4

9

ID: 35612

La funksjonen f være gitt ved

f (x) = x^{3}

a) Bruk formelen

{(x^{n})}^{'} = n \cdot x^{n - 1}

til å finne

f^{'} (x)

.
b) Finn vekstfarten i punktet x = 2.

c) Finn ligningen for tangenten i punktet

(2, f (2))

.
d) Tegn grafen til f sammen med tangenten i et koordinatsystem.

10

ID: 83808

Sarah deriverer funksjonen $f (x) = {2 x}^{3} + {4 x}^{2} - 5 x + 8$ på følgende måte:

${f^{'} (x) = ({2 x}^{3})}^{'} + {({4 x}^{2})}^{'} - {(5 x)}^{'} + {(8)}^{'} = {2 x}^{2} + {8 x}^{1} - 5 x + 0 = 2 x^{2} + 3 x$

Rett opp feilene i Sarahs derivasjon.

Fasit

1

ID: 34592

Fasit:

$f^{'} (x) = \frac{21}{5} x^{2} - \frac{2}{3} x - \frac{19}{3}$

2

ID: 33555

Fasit:

$f^{'} (x) = - \frac{2}{3} x + \frac{2}{5}$

3

ID: 49711

Fasit:

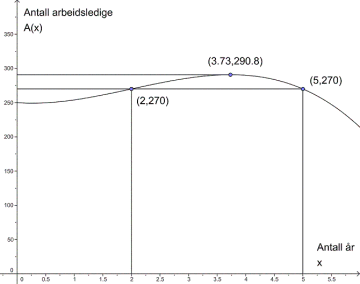
a) Antallet arbeidsledige stiger sakte fram til en topp nås om ca. 4 år. Deretter reduseres antallet relativt raskt, se figur.

b) Høyeste antall ledige er ca. $291$ for $x = 2 + \sqrt{3} \approx 3, 73$ år.

c) Etter $x = 2$ år og $x = 5$ år

d) $14, 4 %$ nedgang

4

ID: 83848

Fasit:

$p^{'} (t) = x^{3} + x$

Den derivertes deriverte $p^{''} (t) = {3 x}^{2} + 1$

5

ID: 49698

Fasit:

a) $y = - 4 x + 5$

b) $y = 8 x - 11$

c) Ingen parallelle til tangenten i a).

Én parallell til tangenten i b): $y = 8 x + 21$ , som tangerer $f$ for $x = - 2$ .

6

ID: 83760

Fasit:

7

ID: 35644

Fasit:

a) 7.33 m og 18.67 m
b)

h^{'} (t) = - \frac{1}{10} t^{2} + 5 t

c) 60 cm per år og 40 cm per år.

8

ID: 35602

Fasit:

f^{'} (x) = - 3

9

ID: 35612

Fasit:

a) 3x²
b) 12
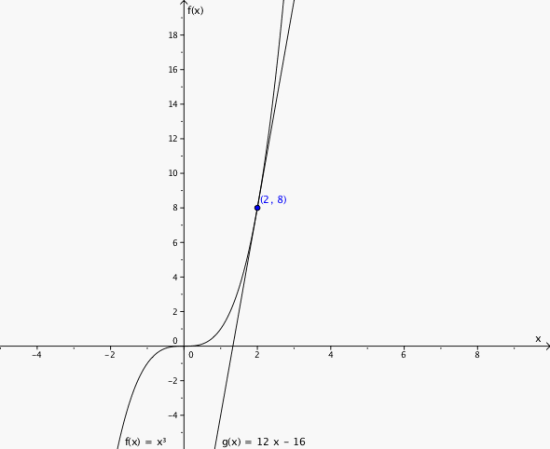
c) y = 12x - 16

10

ID: 83808

Fasit:

$f^{'} (x) = {6 x}^{2} + 8 x - 5$