Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Bestem ved hjelp av digitalt verktøy, toppunktet på grafen til
2
Overskuddet ved produksjon og salg av mp3 - spillere er gitt ved
.
O(x) er overskuddet i kroner når det blir produsert x enheter per uke.
Hvor mange enheter gir størst overskudd? Hva er det største overskuddet?
3
La være funksjonen .
a) Hvorfor kan man med en gang se at grafen til går gjennom origo?
b) Hvilke andre nullpunkter har ?
c) Finn topp- og bunnpunktene til .
4
Bestem ved hjelp av digitalt verktøy, toppunktet på grafen f :
5
6
En ball kastes loddrett oppover. Høyden over bakken i meter etter sekunder er gitt ved . Funksjonen er definert for alle frem til og med ballen treffer bakken.
a) Når treffer ballen bakken?
b) Hva er den deriverte av funksjonen?
c) Hva blir den største høyden ballen når? Når er den ved maksimalhøyden?
7
Vi har funksjonen .
a) Finn nullpunktene til .
b) Finn nullpunktene til .
c) Hva er den momentane veksten til for ?
d) Hva er den gjennomsnittlige veksten til fra til ?
e) Tegn fortegnsskjema for , og vis at har et toppunkt i .
8
En fastfood-kjede skal lansere en ny hamburger. De er usikre på hvilken pris burgeren bør ha, men den minste prisen den kan ha er kr. Basert på en markedsundersøkelse, tror de at antall solgte burgere per butikk per uke vil avhenge av prisen i tråd med funksjonen
,
der er prisen i kr.
a) Hvor mange burgere blir i gjennomsnitt solgt per butikk på en uke hvis prisen er kr?
b) Anta at det er seks restauranter i kjeden. Sett opp en funksjon som gir inntekten til kjeden per uke når er prisen i kr.
c) Hvilken pris gir maksimal inntekt, og hva blir maksimal-inntekten? Løs grafisk på lommeregneren.
9
10
Funksjonen f er gitt ved:
a) Tegn grafen til f på lommeregneren.
b) Finn bunnpunktet og toppunktet til f.
Fasit
1
2
Ved produksjonen av 450 enheter er overskuddet størst. Og da er overskuddet på 9125 kr.
3
a) , siden alle ledd inneholder .
b)
c) Bunnpunkt:
Toppunkt:
4
( - 2, - 2 )
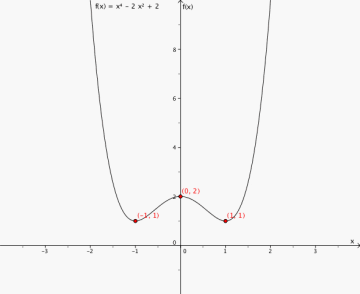
5
toppunkt (0,2)
bunnpunkter (-1,1) og (1,1)
Grafen synker når x<-1 og når 0
6
a) Etter sekunder.
b)
c) meter etter sekunder
7
a)
b)
c) i begge.
d)
e) Forttegnsskjemaet viser at har et toppunkt i og .
8
a) burgere
b)
c) kr, som gir kr.
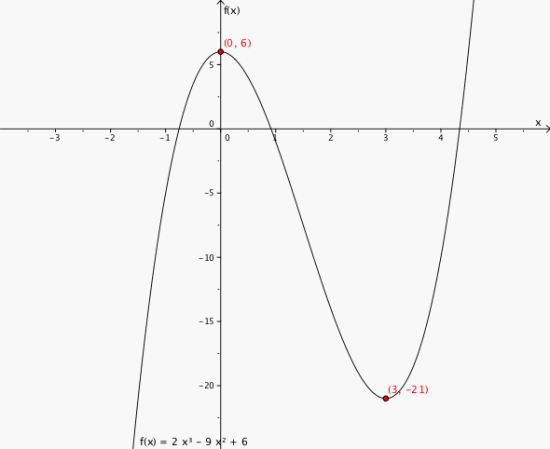
9
Toppunkt (0,6)
Bunnpunkt (3,-21)
Grafen stiger når x<0 og når x>3- Grafen synker når 0
10
b) toppunkt (-2,16), bunnpunkt (2,-16)