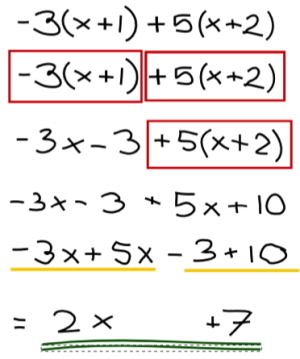Algebra med fargede lapper
Noen elever blir nærmest paniske når de ser lange algebraiske uttrykk. Det å vite hvordan en skal sette i gang, holde oversikt og få struktur i arbeidet med algebraiske uttrykk er en krevende prosess. Undervisningsopplegget viser en måte elevene kan øve på denne prosessen. Vi bruker fargede papirlapper og noen enkle regler knyttet til disse.
Lærerens instruksjoner
Målet er å gi eleven trening i å jobbe med lengre algebraiske uttrykk på en ryddig måte. Eleven får konsentrere seg om ett ledd om gangen og jobber seg gjennom de røde, gule og grønne lappene. Det anbefales at læreren viser fremgangsmåten i et eksempel i hel klasse før elevene setter i gang på egenhånd. Begynn gjerne med enkle uttrykk uten doble parenteser eller parenteser som multipliseres med hverandre. Elever oppfordres til å følge reglene nøyaktig.
I den første økten jobber elevene med fysiske lapper, mens i timene som følger abstraheres metoden slik at denne blir en naturlig del av arbeid med algebraiske uttrykk.
DEL 1
Finn et enkelt algebraisk uttrykk. Denne skal brukes som et eksempel. Begynn med å minne elevene på forskjellen mellom en faktor og et ledd i et uttrykk. Husk også å forklare for dem at hvis det ikke står minus foran et uttrykk, betyr det at det er positivt, altså det står egentlig + foran uttrykket men det til vanlig skrives det ikke. Dette er viktig da enhver lapp skal begynne med + eller -.
Elevene får utlevert oppgaver og lapper. Eleven tar en rød lapp, og skriver på lappen det første leddet i uttrykket (husk eventuelt + foran). Når eleven har kommet frem til neste + eller - som står utenfor en eventuell parentes, tar hun en ny rød lapp og skriver tegnet og det påfølgende leddet. Eleven fortsetter på denne måten til hele uttrykket er skrevet ned på røde lapper. Hvis reglene er fulgt, vil nå hver rød lapp inneholde ett ledd av det opprinnelige uttrykket med + eller - foran seg. Eksempelvis gir uttrykket tre røde lapper; og .
Eleven velger en av de røde lappene. Hun løser opp alle parentesene (på et kladdeark). Det nye uttrykket uten parenteser skrives på en gul lapp. Hun gjentar dette til det ikke er flere røde lapper igjen. Nå sitter hun med like mange gule lapper som hun hadde av røde lapper. Disse gule lappene klippes opp slik at hver ny lapp starter med + eller - etterfulgt av et enkelt ledd.
Gule lapper med samme type ledd (konstanter, ledd med x,...) samles i hver sin haug. Eksempelvis gir de tre røde lappene og fire gule lapper og . Det lages to hauger; haugen med og , og haugen med og .
Uttrykkene på alle gule lapper i en haug trekkes sammen. Svaret skrives på en grønn lapp. Eleven gjør det for alle hauger. Når eleven er ferdig, vil det være like mange grønne lapper som hauger med gule lapper. De grønne lappene legges etter hverandre og eleven har svaret.
DEL 2
I del 2 skal metoden med farget papir gjøres mer abstrakt. Dette er et skritt på veien for å kunne løse opp uttrykkene uten de fysiske hjelpemidler (papirlappene). Lappene blir tegnet inn i uttrykket. Elevene kan gjerne i begynnelsen bruke røde, gule og grønne fargeblyanter til å markere uttrykkene som står på lappene. Etterhvert skal de gå over til å tegne med blyant, og til slutt bare forestille seg firkantene uten å tegne disse inn. For å ha en referanse, får elevene utdelt reglene for de forskjellig fargede lappene (se i Elevens oppgaveark).
Elevens oppgaveark
Del 1
Nå skal du løse oppgavene ved å bruke gule, røde og grønne lapper etter reglene som følger. Her er det viktig at du leser og følger reglene nøye!
| Røde lapper: |
| • En lapp begynner ALLTID med enten + eller -. • Det står bare ett ledd på en lapp. • På en lapp skal hele parentesen (og det som står inne i denne) stå. |
Ta en rød lapp. Løs nå opp alle parentesene på den røde lappen - bruk et kladdeark.
Ta en gul lapp og se under på reglene for gule lapper.
Gjør det samme for alle de røde lappene du har.
| Gule lapper: |
| • Du tar én gul lapp for hver røde lapp du har. • Hver lapp skal starte med + eller -. • Ingen gule lapper skal ha parentes! |
Er alle gule lappene ferdigskrevet?
Klipp opp disse slik at
- hver ny gul lapp begynner med + eller - OG
- på hver lapp er det kun én enten + eller -.
Fordel lappene i hauger slik at lappene med samme bokstav ligger i en haug, lappene med tall ligger i en annen haug og så videre.
Velg én haug, og legg sammen uttrykkene på lappene.
Ta en grønn lapp og skriv ned svaret.
Gjør dette med alle haugene.
Hvis du har gjort alt over riktig, er reglene for de grønne lappene automatisk oppfylt:
| Grønne lapper: |
| • Hver lapp skal ha maks én bokstav (eller produkt av bokstaver). • Ingen lapper skal ha samme bokstav eller produkt av bokstaver. |
Gratulerer! Du har nå løst opp og trukket sammen det algebraiske uttrykket. Svaret står på de grønne lappene!
Del 2
- Skriv ned uttrykket du skal jobbe med.
- Tegn (røde) firkanter som viser hva ville stått på de røde lappene.
- Løs opp parentesene i hver av firkantene for seg. Jobb med bare én firkant om gangen. (husk at det som er inne i én firkant ikke kan påvirkes av det som er utenfor den samme firkanten).
- Skriv ledd med like bokstaver (og tegn som står foran disse) etter hverandre. Tegn en (gul) strek under hver samling (Tenk på hvilke ledd som ville ligge i samme gule haug).
- Trekk sammen ledd som er like og sett to (grønne) streker under svaret.
Aktuelle kompetansemål i læreplanen (LK06)
Læreplan i matematikk fellesfag
- Etter 10. årssteget
- Tal og algebra
- utvikle, bruke og gjere greie for ulike metodar i hovudrekning, overslagsrekning og skriftleg rekning med dei fire rekneartane
- behandle, faktorisere og forenkle algebrauttrykk, knyte uttrykka til praktiske situasjonar, rekne med formlar, parentesar og brøkuttrykk og bruke kvadratsetningane
- Tal og algebra
Når, hvor og hvordan
-
Klassesituasjon
Enkeltvis eller i par.
-
Utstyr
Del 1: Rødt, gult og grønt papir (helst klippet opp i mindre lapper på forhånd), sakser, oppgaveark, skrivesaker, røde, gule og grønne fargeblyanter og kladdepapir.
-
Tidsbruk
En dobbeltime (del 1) og en enkelttime (del 2).
-
Valg av tidspunkt
Etter at elevene har fått innføring i hvordan man trekker sammen algebraiske uttrykk, løser opp parenteser og liknende.