Målestokk
Vi bruker målestokk for å lage mindre eller større modeller av ting - og målestokken sørger for at forholdet mellom størrelsene er den samme på modellen og i virkeligheten.
Om vi skal tegne et kart, er det viktig at forholdet mellom avstanden på kartet og avstanden i virkeligheten er den samme på kartet. Når vi tegner et kart, forminsker vi størrelsene. Om vi heller skal lage en stor statue av en person, er det også viktig at størrelsesforholdet er det samme på hele statuen. I dette tilfellet forstørrer vi.
Vi gir nå en presis definisjon av
Målestokk
Målestokken angir hva en måleenhet på for eksempel kartet svarer til i terrenget.
Eksempel:
Et kart har målestokken 1 : 25000 (leses: en til tjuefemtusen)
Dette betyr for eksempel at:
| - | 1 cm på kartet tilsvarer 25000 cm i terrenget (25000 cm = 250 m) |
| - | 1 dm på kartet tilsvarer 25000 dm i terrenget |
| - | 4 cm på kartet er 25000 · 4 cm i terrenget (25000 · 4 cm = 100000 cm = 1000m = 1 km). |
Eller mer generelt:
1 bestemt måleenhet på kartet er 25000 slike måleenheter i terrenget.
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Avstand til nærmeste vann
Du har nettopp kommet til hytta. Hytta har ikke verken innlagt vann, wifi eller dekning. Du må derfor til nærmeste elv for å hente vann. På bordet står det et kart med målestokk . Du måler med linjal at det er på kartet fra hytta til nærmeste elv. Siden målestokken er , betyr det at på kartet er i virkeligheten. Vi vet at det er i en meter, så det betyr at på kartet er meter i virkeligheten. Det vil si at på kartet er meter i virkeligheten. Siden det er meter i en kilometer, er det fra hytta til nærmeste elv. La oss håpe du finner en bekk på veien!
Plantegning
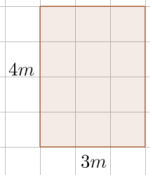
Du vil tegne en tegning av rommet ditt. Rommet ditt er stort. Vi bruker en målestokk på , og vi lurer på hvor stor tegningen blir.
Rommet er , og er derfor formet som du ser på figuren til venstre. Siden målestokken er på , betyr dette at meter på kartet er meter i virkeligheten. Vi merker at meter blir altfor stort å jobbe med, så vi jobber heller med centimeter: centimeter på kartet er centimeter i virkeligheten.
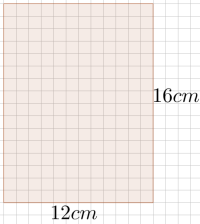
Vi vet at det er centimeter i en meter, dermed vil centimeter på kartet være centimeter på kartet, altså meter. meter i rommet vil da svare til centimeter på kartet. Siden rommet er stort, vil kartet ha en størrelse på , siden og . Da kommer kartet ditt til å være formet slik:
Merk at rommet og kartet har samme form, men ulik størrelse!
Lag en statue
Vi skal lage en statue av en kjent person, og vi vil at statuen skal være meter høy. Vi vet at personen er meter høy, og lurer på hvilken målestokk vi skal bruke.
Siden personen i virkeligheten er meter høy, og statuen er meter høy, kan vi bruke dette til å si at meter på statuen tilsvarer meter i virkeligheten. Da får vi en målestokk på . Når vi jobber med målestokk er det vanlig at det minste tallet er . Da kan vi dividere begge sider på for å få . Altså statuen er 10 ganger så stor som kjendisen er.
Er plantegningen riktig?
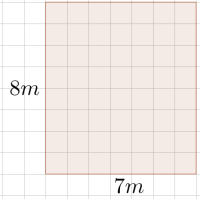
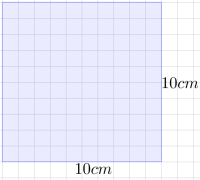
Et klasserom er stort:
En medelev tegner et kart av klasserommet på og spør deg om han har gjort det rett.
Vi merker at dette umulig kan være riktig. På den ene siden vil på kartet svare til i virkeligheten. Da , gir dette en målestokk på , og multipliserer vi begger sider med får vi . På den andre siden må på kartet også svare til . Dette gir en målestokk på . Dermed kan ikke eleven ha brukt samme målestokk på hele kartet.
Dette kan vi også se geometrisk. Klasserommet er formet som et rektangel, mens kartet er formet som et kvadrat. Forholdet mellom bredde og lengde er ikke det samme! Da kan eleven umulig ha brukt samme målestokk på hele kartet.
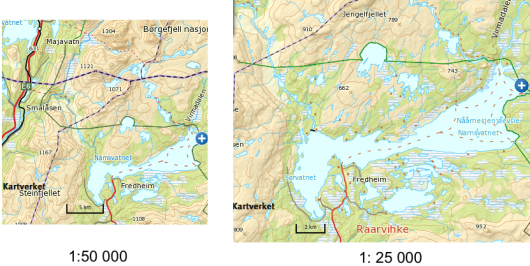
Mer detaljert turkart
Vi planlegger en tur i Børgefjellet nasjonalpark. Vi vurderer om vi skal gå rundt Namsvatnet på sørsiden eller nordsiden? Vi ønsker å unngå myr (hvite områder med parallelle blå streker over).
Vi har et kart med målestokk , og det er tilsynelatende ingen myr på norsiden av vannet. For at vi skal være sikre på dette, ønsker vi et utdrag av kartet som kun viser halvparten av området det originale kartet viser.
Vi ønsker altså å forstørre området. Da vil på det nye kartet svare til på det gamle. Vi kan dividere med to og si at på det nye kartet svarer til på det gamle. Det gir oss en målestokk på .
To turkart
Fremme ved tavlen i klasserommet ditt er det et kjempestort kart. Det står at målestokken er . I geografitimen deler læreren ut kopier av det samme kartet. Du regner ut at kopien din er ti ganger mindre. Hvor stor er målestokken på kartet du har i hendene?
på det store kartet svarer til på kartet ditt. Siden på det store kartet er , har det lille kartet ditt målestokk .
Del på Facebook
Lynkurs, 8.-10.trinn
Målestokk og forholdsregning
Består av:
- Målingsforhold
- Målestokk
- Operaen i Oslo