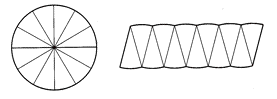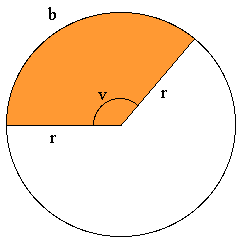Alt om sirkel
Tallet har vært kjent for mennesket så langt tilbake som til da det ble bygget pyramider i Egypt.
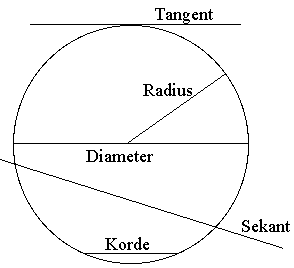
Sirkel
En sirkel deler planet i to områder, akkurat som mangekantene gjør det: en indre sirkelflate og et ytre område. Noen ganger mener vi sirkelflaten når vi sier sirkel. For eksempel er det helt vanlig å snakke om arealet til en sirkel. Selve kurven som danner sirkelen, kalles da periferien.
La oss se på noen viktige begreper.
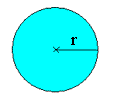
a Et linjestykke fra sentrum til et punkt på en sirkel kalles en radius.
b To radier sammen med sirkelbuen mellom dem, begrenser en sektor.
c Ei linje som skjærer sirkelen i to punkter, kalles en sekant.
d En korde er et linjestykke mellom to punkter på sirkelen. En korde som går gjennom
sentrum, er en diameter.
e Ei linje som bare berører sirkelen i ett punkt, kalles en tangent til sirkelen.
Vi legger merke til to egenskaper ved sirkelen:
− Enhver linje gjennom sentrum deler sirkelen i to like deler, halvsirkler.
− Hvis punktene og ligger på en sirkel, og er sentrum i denne sirkelen, så bestemmer punktene en trekant som er likebeint.
Tallet
Alle sirkler har samme form. Det betyr at forholdet mellom omkrets og diameter er det samme for alle sirkler. Dette forholdet har fått et spesielt symbol, den greske bokstaven (leses pi).
er det tallet vi får til svar hvis vi måler omkretsen på en sirkel og dividerer denne på diameteren til sirkelen.
Hvis vi gjør målinger på sirkler og finner ut hvor stort tallet er, vil vi få et svar litt i overkant av . I virkeligheten kan vi ikke skrive tallet helt eksakt som et desimaltall, men gode tilnærminger til er og .
Omkrets og areal av en sirkel
Forholdet mellom omkrets og diameter i sirkler er konstant, og lik tallet . Siden diameteren er dobbelt så stor som radien, er forholdet mellom omkretsen og radien lik . Vi har altså at
For å beregne arealet til ei sirkelflate, deler vi sirkelflaten inn i mange like store sektorer, klipper disse ut og plasserer dem ved siden av hverandre slik:
Hvis vi gjør disse sektorene svært smale, ser vi at sirkelens areal vil bli det samme som arealet til et parallellogram. Mer presist er det grensetilfellet ved uendelig mange, uendelig smale sektorer, et rektangel med lengde lik halvparten av sirkelens omkrets, og bredde lik sirkelradien.
Det betyr at vi får sirkelens areal
Resultat er at formelen for arealet til en sirkel med radius blir:
Eksempel 1.
En sirkel har radius . Regn ut omkrets og areal.
Vi setter inn i formlene og får:
Sirkelsektor
Noen ganger kan det være bruk for å beregne arealet av en sirkelsektor.
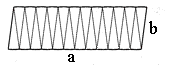
Hele sirkelbuen er . Hvis en sektor spenner over en bue med gradtall , betyr det at vinkelen som dannes av de to radiene er lik . Arealet av sektoren er like stor del av hele sirkelens areal som buen er av hele sirkelens omkrets.
Brøken angir hvor stor del av sirkelen sirkelsektoren utgjør. En sektor med buelengde på én grad har dermed et areal som er lik . Vinkelen angir hvor mange slike deler sirkelsektoren består av. På figuren har vi kalt buelengden for . Hvis vi kjenner , kan vi finne arealet av sirkelsektoren ved hjelp av den. Hele omkretsen har jo en lengde på , og arealet til sektoren blir
Legg merke til at formelen likner formelen for arealet av en trekant med grunnlinje og høyde .
Del på Facebook
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Diameter
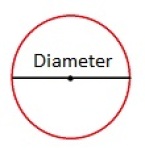
En rett linje som forbinder to punkter på sirkelbuen og som samtidig går gjennom sentrum.
Lengden av en diameter, d, er lik to radier, r. d=2r. -
Korde
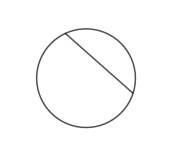
Et rett linjestykke som forbinder to punkter på en sirkel. Den lengste korden til en sirkel er diameteren.
-
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Linjestykke
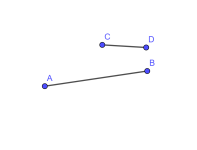
Et linjestykke er en sammenhengende bit av en linje, avgrenset av to endepunkter. Navnet på et linjestykke er vanligvis gitt ved de to endepunktene: AB, CD, ...
-
Omkrets
Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter. -
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.
-
Punkt
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
-
Radius
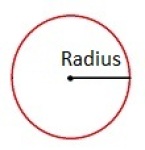
Radius er en rett linje fra sentrum av en sirkel eller kule og ut til sirkellinja eller kulens overflate. Radius sin lengde er den samme, uansett hvor på sirkelen eller kulen du måler.
-
Sekant
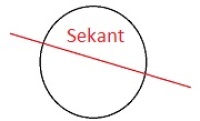
En linje som skjærer en kurve. En korde er en del av en sekant. En sekant er ikke det samme som en tangent.
-
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.Areal:
Omkrets: -
Sirkelbue
Er en sammenhengende del av sirkellinjen.
-
Sirkelsektor
Se Sektor
-
Tangent
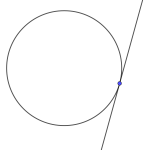
Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.