Forskjellige typer vinkler
Vi har rette vinkler, spisse vinkler, supplementvinkler og mange flere. En snekker, arkitekt, elektriker, rørlegger, ingeniør og andre fagarbeidere kjenner godt til de ulike typene vinkler og bruker disse til daglig.
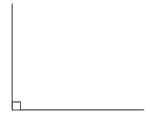
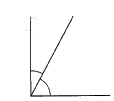
Rette vinkler
En rett vinkel er akkurat , fjerdeparten av et helt omløp. Vi tegner vanligvis en bue for å markere en vinkel. Men når vinkelen er rett, altså , markeres vinkelen med et lite kvadrat, som angitt i figuren.
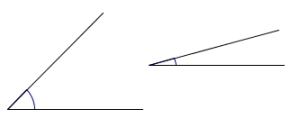
Spiss vinkel
|
En vinkel som er mellom og kalles en spiss vinkel. |
|
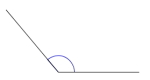
Stump vinkel
|
En vinkel som er mellom og kalles en stump vinkel. |
|
Supplementvinkler, nabovinkler og komplementvinkler
To vinkler som er til sammen kalles supplementvinkler. To stråler i motsatte retninger ut fra ett punkt på ei rett linje danner en -graders vinkel. En tredje stråle ut fra samme punkt deler en -graders vinkel i to, og de to vinklene kalles nabovinkler. Nabovinkler er dermed supplementvinkler som har en spesiell plassering i forhold til hverandre: De har ett vinkelbein felles.
|
|
To vinkler som til sammen er på kalles komplementvinkler. |
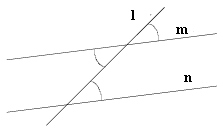
Samsvarende vinkler
Når ei linje skjærer to andre linjer, og , kommer det fram mange vinkler. Vinkler som har forskjellig toppunkt, men der begge har høyre eller venstre vinkelbein langs overskjæringslinja , kalles samsvarende vinkler. Da er følgende en grunnleggende sammenheng:
Samsvarende vinkler er like store hvis og bare hvis de to overskårne linjene er parallelle.
Vi kan se at det må være slik ved å rotere hele figuren om midtpunktet mellom de to skjæringspunktene.
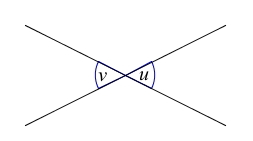
Toppvinkler
To stråler i forskjellige retninger ut fra ett felles endepunkt danner en vinkel. Det felles punktet kalles vinkelens toppunkt, og strålene kalles vinkelbein. Området mellom vinkelbeina kalles vinkelområde. Vinkler som har felles toppunkt, og som har vinkelbein i stikk motsatt retning, kalles toppvinkler.
Her er , fordi strålene krysser hverandre og danner to toppvinkler på hver side.
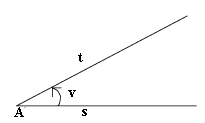
Dynamisk vinkel
Vinkler kan vi see på som et dynamisk begrep. Hvis vi bruker rotasjon, får vi et vinkelmål med fortegn som markerer dreieretningen.
Vi ser på to stråler, og , med samme startpunkt . La oss forestille oss at strålene i utgangspunktet dekker hverandre. Det er da ingen vinkel mellom dem, eller vi kan si at vinkelen er (null grader). Deretter lar vi ligge fast, og lar rotere om mot klokka til den ligger slik figuren viser. Det er nå en vinkel mellom de to strålene.
På neste tegning, har vi latt rotere et helt omløp om . Det er så langt vi kan rotere før vi begynner på nytt igjen.
En slik rotasjon helt rundt danner en vinkel på . Som vi ser av tegningen spenner vinkelen over en hel sirkel. Sirkelen er dermed delt opp i .
Del på Facebook
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Firkant
En firkant er en geometrisk figur med fire hjørner og fire sidekanter.
-
Komplementvinkler
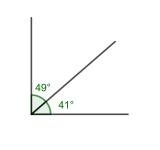
To vinkler som til sammen er 90°.
-
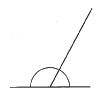
Like vinkel
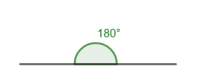
En vinkel på 180 grader kalles en like vinkel.
-
Mangekant
En mangekant er en geometrisk lukket figur som er satt sammen av rette linjestykker. Kalles også en polygon.
Eksempel: trekant, firkant, femkant (pentagon) og sekskant (heksagon).
-
Nabovinkler
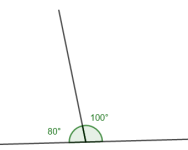
To vinkler som ligger ved siden av hverandre, har et felles vinkelbein og utgjør 180° tilsammen.
-
Rett vinkel
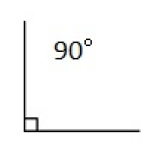
En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.
-
Samsvarende vinkler
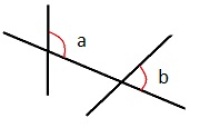
To vinkler som enten har venstre vinkelben eller høyre vinkelben felles. Samsvarende vinkler behøver ikke være like store.
Eksempel: ∠a og ∠b er samsvarende vinkler, fordi de har høyre vinkelben felles.
-
Sirkel

Sirkel brukes i to betydninger:
1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.
2) Flaten som sirkellinjen begrenser.Areal:
Omkrets: -
Skjæringspunkt
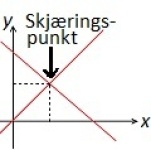
Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
-
Spiss vinkel
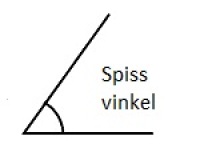
En spiss vinkel er mellom 0° og 90°.
-
Spissvinklet trekant
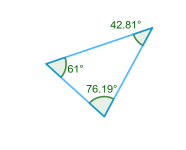
Trekant der alle vinklene er spisse, dvs. alle vinklene er mellom 0° og 90°.
-
Stump vinkel

En stump vinkel er mellom 90° og 180°.
-
Supplementvinkler
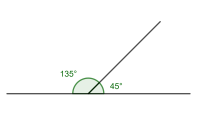
To vinkler som til sammen er 180°.
-
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
-
Vinkel
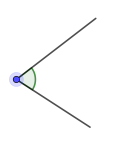
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.
-
Volum
Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).