Primtall og faktorisering
Ved kryptering bruker vi store primtall til å skjule passord, bankinformasjon og annet på nettet. Hackere lager programmer som finner disse primtallene, "knekker koden", og får tak i informasjonen. Jo mer vi vet om primtall, desto sikrere er informasjonen på nettet.
Primtallene er byggesteiner for alle naturlige tall. Når vi skal finne fellesnevneren til store brøkuttrykke eller forkorte brøker, bruker vi primtallsfaktorisering.
Hva er primtall?
Vi sier at et tall er delelig med et annet tall dersom kvotienten, det første tallet delt på det andre, er et helt tall. For eksempel er 12 delelig med 3, siden kvotienten er 4. 12 er derimot ikke delelig med 8, siden kvotienten er 1,5.
DEFINISJON
Et primtall er et tall som er større enn 1 og som kun er delelig med seg selv og 1.
Fordi tallet 1 ikke er definert som primtall, er 2 det minste primtallet. Tallet 2 er også det eneste partallet som er et primtall. Alle andre partall er jo delelige med 2.
Primtallene mellom 1 og 20 er 2, 3, 5, 7, 11, 13, 17, 19.
Et av de viktigste og mest grunnleggende resultatene i matematikk kalles
TALLTEORIENS FUNDAMENTALSETNING
Alle naturlige tall utenom tallet 1, som selv ikke er et primtall, kan faktoriseres slik at alle faktorene er primtall, og denne faktoriseringen er entydig.
Å skrive et tall som et produkt av primtall kalles å primtallsfaktorisere. Et tall kan primtallsfaktoriseres på bare én eneste måte, sett bort fra at rekkefølgen på faktorene kan variere. Etter å ha primtallsfaktorisert et tall, vet vi med sikkerhet at dette ikke kan gjøres på noen annen måte.
Eksempel 1.
12 er et partall og derfor delelig med 2. Tallet 2 er et primtall: .
6 også er et partall. Så vi faktoriserer igjen:
Her er alle faktorene primtall. Da er vi er ferdige og har funnet den eneste mulige primtallsfaktoriseringen.
Eksempel 2.
Tallet 17 er ikke delelig med noe mindre tall, utenom med 1. Sjekk det! Derfor er 17 et primtall.
Eksempel 3
Dermed er .
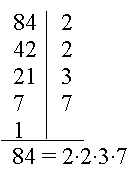
Vi undersøker tallet 84. Dette er et partall og derfor delelig med 2:
42 er også et partall. Vi dividerer med 2 igjen og får at
Da kan vi skrive
.
21 er produktet av 3 og 7 og derfor heller ikke et primtall. Men både 3 og 7 primtall, og den endelige primfaktoriseringen av 84 er
. En praktisk oppstilling ved primtallsfaktorisering ser du på bildet.
Primtallsfaktorisering og brøk
Eksempel 4.
Forkort brøken .
Vi begynner med å primfaktorisere telleren og nevneren:
Brøken kan vi skrive som .
Både i telleren og nevneren har vi tallet 3 og derfor kan vi fortkorte. Vi får
.
Telleren og nevneren har ikke lenger noen felles faktorer, og brøken kan ikke forkortes ytterligere.
Eksempel 5
Regn ut
For å legge sammen to brøker, finner vi først fellesnevneren. En måte å gjøre dette på er å multiplisere de to nevnere, men da får vi et stort tall og det er fort gjort at vi under utregningen gjør feil. Så la oss se primtallsfaktorisere hver nevner:
Vi ser at 2 og 3 er fellesfaktorene for nevnere. Fellesnevneren er produktet av fellesfaktorene og resterende faktorer slik at fellesnevneren er lik
.
Nå kan vi legge sammen brøkene:
Både telleren og nevneren i svaret er partall og derfor delelig med 2, så vi kan forkorte brøken:
Dette er det endelige svaret da brøken ikke kan fortkortes mer.
Del på Facebook
Begrep
-
Brøk
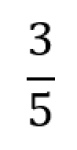
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Faktor
I en multiplikasjon kalles tallene faktorer. Resultatet kalles et produkt.
Eksempel: 5 · 3 = 15. Her er 5 og 3 er faktorer. Tallet 15 er produktet. Vi kan si at 15 består av faktorene 5 og 3.
-
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
-
Naturlige tall
De positive heltallene 1, 2, 3, 4...
Mengden av naturlige tall angis med symbolet .
Hvis 0 skal være med i mengden bruker vi symbolet .
-
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.
-
Primtall
Positive hele tall større enn 1, som kun er delelig med 1 og seg selv.
Ti fem første primtallene er: 2, 3, 5, 7, 11.
-
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.