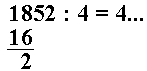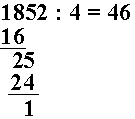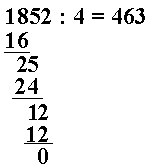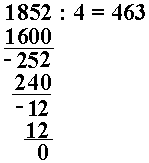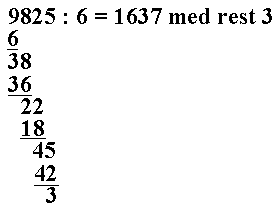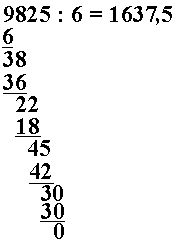Divisjon
Hva er divisjon?
Regnetegnet for divisjon er og det leses dividert med. Resultatet av divisjon kalles kvotient. Tallet som skal divideres kalles dividend og tallet som deler divisor. Divisjon og multiplikasjon er motsatte eller inverse regneoperasjoner, akkurat som addisjon og subtraksjon. Multipliserer vi et tall med et annet, og dividerer deretter tallet med det samme som vi multipliserte med, kommer vi tilbake til det opprinnelige tallet.
Delingsdivisjon og målingsdivisjon
Med utgangspunkt i konkrete situasjoner oppdager vi at det er to typer problemer som svarer til divisjon – eksempel:
- Kristine har 18 roser som hun vil dele likt i tre buketter. Hvor mange blir det i hver?
- Kristine har 18 roser som hun vil dele likt i buketter med tre i hver bukett. Hvor mange buketter blir det?
Det første kalles delingsdivisjon, det andre målingsdivisjon. Ved delingsdivisjon vet vi hvor mange det skal fordeles på. Svaret forteller hvor mange det blir til hver. Ved målingsdivisjon sier divisor hvor mange det skal være i hver mengde. Svaret er hvor mange det rekker til.
Som multiplikasjon kan tenkes som gjentatt addisjon, kan divisjon tenkes som gjentatt subtraksjon: Hvor mange ganger kan 3 subtraheres fra 18?
Eksempel 1.
Du kjøper tre bøker uten å se på prisen. Etter å ha betalt 210 kroner i kassa, regner du raskt ut at hver av bøkene må koste kroner.
Én bok koster 70 kroner. Multiplikasjon og divisjon er motsatte regnearter:
.
Enkelte ganger har vi jo ikke kalkulator tilgjengelig når vi trenger å dividere. Nå skal vi se på hvordan vi stiller opp divisjonsregnestykker. En forutsetning for å forstå divisjon, er å kunne godt gangetabellene.
Eksempel 2.
Fire venner drar sammen på ferie. De får grupperabatt på flyet og betaler samlet 1852 kroner. Hvor mye blir det på hver?
Utregningen kan gjennomføres trinn for trinn slik:
|
Vi kan ikke dele 1 på 4.
|
Vi trekker ned sifferet 5 i 1852 og dividerer 25 på 4.
| med 1 til rest |
Vi trekker ned sifferet 2, det siste sifferet i 1852, og dividerer 12 på 4.
Hva er det så som ligger bak denne metoden? Jo:
betyr i oppstillingen egentlig . Vi finner hvor mange hele hundre hver skal betale, og ser at det blir 4 hundre. Det er 2 hundrere igjen. Dette er det samme som 20 tiere. Det betyr at det i alt er 25 tiere som skal fordeles. Altså er en kort skrivemåte for (25 tiere : 4). Og når vi har plassert 6 tiere på hver, blir det 1 tier igjen. 1 tier pluss 2 kronestykker – da er det til slutt 12 kroner å fordele.
Vi kan skrive resonnementet slik:
|
400 på hver 60 på hver 3 på hver I alt 400 + 60 + 3 = 463 kr på hver. |
Hva skjer så når divisjonen ikke går opp?
Eksempel 3.
Vi velger talleksemplet .
Følger vi oppstillingen fra foran, får vi
Hvis det her dreier seg om å fordele penger, kan vi nå bare tenke de 3 kronene til rest som 30 tiører, og fordele videre. Det blir 5 tiører = 0,5 kr på hver. Da ville oppstillingen blitt slik:
Hvis det ennå hadde vært noe igjen, kunne vi bare fortsatt til hundredeler osv.
Del på Facebook
Begrep
-
Addisjon
Er det samme som å legge til, legge sammen eller plusse sammen.
Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +. -
Divisjon
Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.
Eksempel: fordi .
-
Divisjonstegn
Regnetegnet for divisjon er enten : eller / (brøkstrek).
-
Enere
Sifferet som står på enerplassen forteller hvor mange enere det er i tallet.
Eksempel: tallet 286 har 6 enere.
-
Hundredeler
Sifferet som står på hundredelsplassen viser hvor mange hundredeler det er i tallet.
Eksempel: 3,169. Her står sifferet 6 på hundredelsplassen.
-
Kvotient
Resultatet av en divisjon kalles en kvotient.
Eksempel: , her er 4 en kvotient.
-
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·). -
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen. -
Tiere
Sifferet som står på tierplassen forteller hvor mange tiere det er i tallet.
Eksempel: 3847. Dette tallet har 4 tiere.