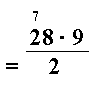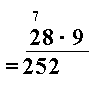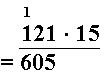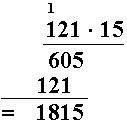Multiplikasjon
Multiplikasjon kan vi tenke på en erstatter av addisjon av flere like ledd. Denne regneoperasjonen hjelper oss å finne svaret raskere når mange like ledd skal legges sammen.
Regnetegnet for multiplikasjon er , og det leses "multiplisert med". Resultatet av multiplikasjon kalles for et produkt. Tallene vi multipliserer sammen kalles faktorer. Hvis det kun er to faktorer, har de egne navn: multiplikand og multiplikator.
Som i addisjon kan vi når vi multipliserer fritt bytte rekkefølgen på faktorene uten at svaret endres. Og vi kan gruppere faktorene slik vi ønsker det selv uten at svaret endres.
| Ombyttingsregel |
| Vi får samme svar når faktorene bytter plass. |
Eksempel 1.
Vi skal regne ut .
Vi kan også velge hvilke tall vi ønsker å multiplisere først
Svaret er 60.
Eksempel 2.
Kåre hadde sommerjobb i to uker à fem dager. Hver dag jobbet han 7 timer. Antallet arbeidstimer i de to ukene kan vi da finne ved enten
- først å regne ut at det blir timer i ei uke og så multiplisere med 2 for å få med begge ukene
eller - å multiplisere 7 timer med de dagene
Tankegangene er dermed, når vi skal regne ut :
Fordelingsregel
En annen viktig sammenheng mellom multiplikasjon og addisjon er fordelingsregelen. La oss se på . Svaret er 56, og vi kan illustrere det.
Vi kan dele opp utregningen i . Dette kaller vi fordelingsregelen.
Vi multipliserer 7 med 8 ved å dele opp 7 i , regne ut og , og til slutt addere svarene.
Fordelingsregelen gjelder naturligvis for alle tall, og den kommer til nytte når tallene er store eller vanskeligere å regne med.
Vi kan, hvis det er ønskelig, også fordele den andre faktoren, for eksempel i slik at:
.
Multiplikasjon av flersifrede tall
Eksempel 3.
Vi skal utføre multiplikasjonen . Noen klarer en slik multiplikasjon i hodet og det er jo kjempe bra! En måte å gjøre dette på er først å finne hvor mye . Vi ser raskt at det er 280. Vi må så trekke fra 28. Regnestykket ser ut som:
.
La oss nå regne ut slik multiplikasjonsregnestykker skal settes opp. Det største tallet settes til venstre. Vi spalter opp hver av tallene i enere, tiere, hundrere og så videre. Vi multipliserer først enerne med hverandre, . Vi noterer 7 som minnesiffer (i mente) på tierplassen, og noterer 2 på enerplassen i svaret.
Så multipliserer vi de to tierne med 9,
. Men husk at vi har 7 i mente slik at vi legger 7 til tierne,
tiere.
Hvordan og hvorfor fungerer dette?
Metoden utnytter fordelingsregelen. Vi deler 28 opp i 8 enere og 2 tiere. Oppstillingen er en kort og grei skrivemåte for denne tankegangen:
.
Eksempel 4.
Regn ut .
En måte å regne dette ut er å tenke på følgende:
blir 1210, og må være halvparten av 1210, altså 605. Da får vi at
.
Vi har delt opp multiplikasjonen i enklere deler ved hjelp av fordelingsregelen.
Vi skal løse oppgaven ved den vanlige oppstillingen. Først tar vi for oss det sifferet som står på enerplassen i tallet til høyre. Vi multipliserer dette tallet med hele tallet som står til venstre. Vi får 1 i mente da .
Neste skritt er å multiplisere sifferet som står på tierplassen i tallet til høyre med hele tallet som står til venstre. Vi plasserer resultatet under det foregående, og forskyver sifrene med en plass mot venstre. Grunnen er at det er tiere vi multipliserer med slik at det første tallet er på tierplassen, det neste på hundrerplassen og så videre.
Del på Facebook
Begrep
-
Addisjon
Er det samme som å legge til, legge sammen eller plusse sammen.
Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +. -
Enere
Sifferet som står på enerplassen forteller hvor mange enere det er i tallet.
Eksempel: tallet 286 har 6 enere.
-
Faktor
I en multiplikasjon kalles tallene faktorer. Resultatet kalles et produkt.
Eksempel: 5 · 3 = 15. Her er 5 og 3 er faktorer. Tallet 15 er produktet. Vi kan si at 15 består av faktorene 5 og 3.
-
Gjentatt addisjon
Gjentatt addisjon er addisjon av samme tall flere ganger. Multiplikasjon kan sees på som gjentatt addisjon.
3 + 3 + 3 + 3 + 3 = 5 · 3 = 15
-
Hundrer
Sifferet som står på hundrerplassen forteller hvor mange hundrere det er i tallet.
Eksempel: 38745. Dette tallet har 7 hundrere.
-
Ledd
I en addisjon kalles tallene som legges sammen for ledd.
Eksempel: , her kalles tallene 8, 3 og 5 for ledd.
-
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·). -
Multiplikasjonstegn
Regnetegnet for multiplikasjon er · .
Noen ganger kan du se multiplikasjonstegnet skrevet som x.Eksempel: 2 · 3 eller 2 x 3
-
Produkt
Produkt er et resultat av en multiplikasjon.
Eksempel: 2 · 7 = 14
14 er produktet, mens 2 og 7 kalles faktorer. -
Siffer
Er symbolene (skrifttegnene) som vi bruker i vårt posisjonssystem for å beskrive ulike tall.
Vi har ti ulike siffer: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
-
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen. -
Tiere
Sifferet som står på tierplassen forteller hvor mange tiere det er i tallet.
Eksempel: 3847. Dette tallet har 4 tiere.