Et punkt og en linje
La oss se på hva et punkt, en linje og et linjestykket er.
Det er viktig å være enige om hva begrepene punkt, linje og linjestykke betyr.
- Et punkt knyttes til en fast posisjon, og et punkt har ingen utstrekning. Vi tegner et punkt som en prikk eller et kryss, og vi bruker vanligvis en stor bokstav som navn på et punkt, for eksempel , .
- En rett linje, som vanligvis bare kalles en linje, har posisjon og retning. Den har utstrekning i én dimensjon. En linje fortsetter uendelig fremover og bakover. Vi bruker en liten bokstav som navn på ei linje: , , ... En linje inneholder uendelig mange punkter.
Nå skal vi se på et par andre viktige begreper i geometrien:
- Et linjestykke er en sammenhengende bit av ei linje, avgrenset av to endepunkter. Vi navngir et linjestykke ved de to endepunktene: , , ...
- Et punkt på ei linje deler denne i to stråler, som bare har dette punktet felles.
- To stråler i forskjellige retninger ut fra ett felles endepunkt danner en vinkel. Det felles punktet kalles vinkelens toppunkt, og strålene vinkelbein. Området mellom vinkelbeina kalles vinkelområde. Vinkler som har felles toppunkt, og som har vinkelbein i stikk motsatt retning, kalles toppvinkler.
- To linjer som ligger i samme plan og som ikke skjærer hverandre, er parallelle.
Eksempel
På figuren over er det et utsnitt av ei linje . På er det merket av tre punkter , og . Disse avgrenser tre linjestykker: ett linjestykke mellom og , ett mellom og , og ett mellom og . Linjestykkets startpunkt og endepunkt bestemmer dets navn. Vi kan kalle linjestykkene på figuren for , og . Hvilket punkt som kalles startpunkt og hvilket som kalles sluttpunkt er uten betydning, og angir det samme linjestykket.
Del på Facebook
Begrep
-
Femkant
Femkant er en geometrisk figur med fem sidekanter.
-
Firkant
En firkant er en geometrisk figur med fire hjørner og fire sidekanter.
-
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Linjestykke
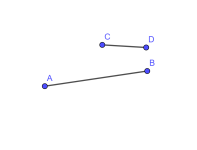
Et linjestykke er en sammenhengende bit av en linje, avgrenset av to endepunkter. Navnet på et linjestykke er vanligvis gitt ved de to endepunktene: AB, CD, ...
-
Mangekant
En mangekant er en geometrisk lukket figur som er satt sammen av rette linjestykker. Kalles også en polygon.
Eksempel: trekant, firkant, femkant (pentagon) og sekskant (heksagon).
-
Plan
Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.
-
Plangeometri
Studiet av geometriske figurer i planet. I den analytiske plangeometrien studeres plane figurer ved bruk av koordinatsystem og algebraiske metoder. Læren om kjeglesnitt er et viktig emne innenfor plangeometri.
-
Punkt
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
-
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
-
Vinkel
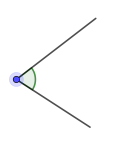
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.





