Addisjon og subtraksjon med brøk
La oss legge sammen eller addere og . Hvordan tenker vi?
|
Tegn brøkene. Til venstre er to av fire delene grønne og til høyre er en av fire delene grønn. Vi er på jakt etter det totale grønne arealet. Hver arealbit er en firedel. Til sammen blir det tre firedeler eller . |
|
|
Samme type argument virker også når vi skal trekke en brøk fra en annen brøk. |
|
La oss se hvordan vi fører regnestykket:
Hvis vi skulle subtrahere fra ville regnestykket sett slik ut:
| Regel |
|
Brøker må ha samme nevner når de adderes eller subtraheres. |
Hvordan regne med brøker som har forskjellige nevnere?
Tenk deg at du skal addere og .
|
Tegn brøkene. Til venstre er en halv av figuren grønn. Til høyre er en av tre deler av figuren grønn. Delene i de to brøkene er ikke like store. Hva gjør vi for å få delene til å bli like store? |
|
| Både to og tre går opp i seks. La oss dele figurene i seks like store biter. | |
|
Nå ser vi at hver av de seks bitene er like stor. Til venstre er nå tre av seks biter grønne. Til høyre er to av seks biter grønne. Vi er på jakt etter det totale grønne arealet. Hver arealbit er en seksdel. Til sammen blir det fem seksdeler eller . |
|
Slik tenker vi når vi skal addere og subtrahere brøker. Regnestykket fører vi opp slik:
Hvis regnestykket var å subtrahere fra , føres regnestykket slik:
Først finner vi fellesnevneren for brøkene. Fellesnevneren for brøkene og er 6, fordi både 2 og 3 går opp i 6. Vi utvider hver av brøkene slik at de får fellesnevneren som nevner. Til slutt adderes eller subtraheres brøkene.
Del på Facebook
Lynkurs, 8.-10.trinn
Brøk
Består av:
- Hva er en brøk?
- Like(verdige) brøker
- Addisjon og subtraksjon med brøk
- Forkorte og utvide brøk
- Multiplikasjon med brøk
- Divisjon med brøk
- Test deg selv i brøk!
- Brøk som areal
Begrep
-
Addisjon
Er det samme som å legge til, legge sammen eller plusse sammen.
Regneoperasjonen 5 + 7 = 12 kalles en addisjon.
Tallene 5 og 7 kalles ledd, og resultatet, 12, kalles en sum.
Mellom leddene skrives plusstegn +. -
Brøk
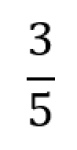
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Halvere
Halvere betyr å dele i to like store deler. Det er det samme som å dividere med 2.
-
Fellesnevner
Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.
Eksempel: , 42 er fellesnevner for disse to brøkene.
-
Subtraksjon
En regneoperasjonen der vi har et tall og trekker fra et annet.
Regneoperasjonen 14 – 9 = 5 kalles en subtraksjon.
Tallene 14 og 9 kalles ledd, og resultatet kalles differensen. -
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi







