Divisjon med brøk
Tegn og tenk
|
Vi har liter melk som skal helles på liters kartonger. Hvor mange kartonger trenger vi? Her blir vi spurt om å finne svaret på eller hvor mange ganger går opp i . Vi kan tegne en halv og halvere hver av delene. Da ser vi at og derfor er . Svaret er 2. |
Tegn og utvid brøken
|
Hvor mange ganger går opp i eller ? |
|
|
Her tegner vi først . Hvis vi deler hver tredel i to like store deler, får vi seksdeler. Vi ser her at 4 seksdeler får plass i det omrdået som er stort. |
|
En annen måte vi kan finne svaret, er å utvide brøken til seksdeler, . Regnestykket ser ut som . Spørsmålet nå er hvor mange seksdeler det er plass i fire seksdeler. Svaret er 4.
Bruk regelen
| Regel |
| Når to brøker divideres på hverandre, snur vi først den andre brøken og multipliserer den med den første. |
Nederst på siden er regelen bevist.
Divisjon med brøk og heltall
Vi har fire liter melk som skal fylles opp i liters kartonger med melk. Hvor mange kartonger trenger du?
Her skal vi regne ut . Fordi vi vet at , vet vi at for hver liter bruker vi tre kartonger. Siden vi har fire liter må vi bruke 12 kartonger. Vi kan også tegne opp en tallinje som vist under og telle oss til svaret
Her kunne vi også brukt regelen. Husk at helt tall kan gjøres om til brøk med nevner lik 1.
Bevis for regel
Regelen kan ved hjelp av bokstaver skrives slik:
Bokstavene a, b, c og d er fire ukjente tall. Brøkstreken i brøken betyr også divisjon. Vi kan skrive 12:4 eller . Begge disse uttrykkene har samme verdi, nemlig 3. Vi benytter oss av dette faktum når vi beviser regelen vår:
Del på Facebook
Begrep
-
Brøk
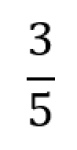
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Divisjon
Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.
Eksempel: fordi .