Mia og Marius og kongebesøket
Mia og Marius havner midt i et arrangement hvor Kongen deltar, og de blir stående og lure på om kortesjen med de svarte "kongebilene" klarer å kjøre den oppsatte ruta slik at de slipper å kjøre en gate mer enn én gang.
Historien
Se på alle de folkene som står og ser på, det ser jo nesten ut som det er 17. mai. Mia og Marius har vært i svømmehallen med resten av familien og er på vei hjem. Tydeligvis har de forvillet seg inn i et eller annet arrangement.
Kongen er her for å åpne det nye sykehjemmet, så det er vel det som foregår. Pappa har god oversikt over begivenhetene.
Der kommer alle de svarte bilene med de morsomme nummerskiltene, A1, A2, A3 og A4, men de kjører ikke i riktig rekkefølge, sier Mia undrende.
Oppgave 1
Bilene i Kongens følge har numrene A1, A2, A3 og A4, men de kjører ikke i rekkefølge. Vi vet at
- de to midterste har sum 5 (f.eks. A1+A4 eller A2+A3)
- de to bakerste har sum 7
- A4 kjører ikke sist
I hvilken rekkefølge kjører de fire bilene?
Det sto i avisen at Kongen skulle kjøre gjennom gatene i sentrum, de hadde til og med tegnet et kart over hvor man kunne stå og se på følget. Kartet ser ut som et rutenett med fire ruter, kan Pappa fortelle.
Hvis det er de gatene de skal kjøre i, er jeg ikke sikker på om det er mulig å kjøre en rute slik at hver gate bare kjøres én gang, skyter Mia inn.
Oppgave 2
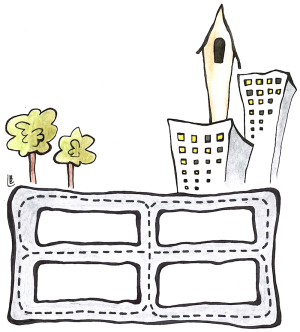
Planen er at Kongen skal kjøre gjennom alle gatene som er tegnet på dette kartet:
Er det mulig å kjøre gjennom alle gatene på en slik måte at ingen gater kjøres to eller flere ganger?
Pappa har lest mer om Kongebesøket.
Etter at de har vært her skal de videre til nabobyen og se en teaterforestilling, deretter kommer de tilbake hit for å spise middag med ordføreren.
Rekker de det da? undrer Marius.
Oppgave 3
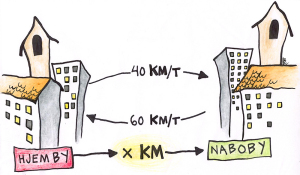
Kongens følge kjører fra hjembyen til Mia og Marius til nabobyen med konstant fart på 40 km/t og tilbake samme vei i 60 km/t. Følget bruker nøyaktig en halvtime kortere tid på tilbaketuren. Hvor langt er det mellom de to byene?
Fasit
Oppgave 1
Det er bare en mulighet for å få sum 7 når vi bare får lov til å bruke tallene 1, 2, 3 og 4 - det er 3 og 4. Siden de to siste bilene skal ha sum 7 og vi vet at A4 ikke kjører sist, må den siste bilen være A3 og nest siste være A4. Så vet vi videre at summen av de to bilene i midten skal være 5, og siden vi allerede har A4 i midten må den andre bilen være A1. Da har vi hele rekkefølgen (forfra og bakover): A2, A1, A4, A3.
Oppgave 2
Nei. Hvis det finnes et kryss der tre gater møtes og vi ikke starter vår rundtur der, må vi ende der. Det er fordi vi kommer i en gate inn til krysset, tar en annen gate ut og så etter hvert kommer vi i den tredje gata tilbake til krysset. Da har vi ingen flere veier å kjøre ut fra krysset og vår ferd må stoppe der. Men i dette rutenettet er det fire kryss med tre gater og vi kan ikke ende opp i mer enn ett av disse.
Oppgave 3
Avstanden er 60 km. Følget bruker halvannen time bort og én time tilbake.
Her kan vi prøve og feile, eller vi kan sette det opp med likninger. Strekningen de kjører til og fra nabobyen er selvsagt like lang hver vei.
Vi prøver oss med at Kongefølget bruker 1 time til nabobyen og 0,5 time hjem igjen. Det gir en strekning på 40 km til nabobyen og 30 km hjem igjen - dette kan ikke stemme.
Så kan vi prøve oss med 2 timer til og 1,5 time hjem. Det gir 80 km til og 90 km hjem - det stemmer heller ikke, men det må være et sted i mellom 1 og 2 timer til nabobyen.
Med 1,5 time til og 1 time hjem finner vi at veien mellom de to byene er 60 km lang.
Bruker vi uttrykket for fart, , får vi to likninger for samme strekning, nemlig (på vei til nabobyen) og (på vei hjem igjen).