Julekalender 2008, 5.-7. trinn
Lærerens instruksjoner
ALT DU FINNER PÅ DISSE NETTSIDENE KAN DU LASTE NED I ET UTSKRIFTSVENNLIG FORMAT (pdf), se vedlegget i høyrespalten.
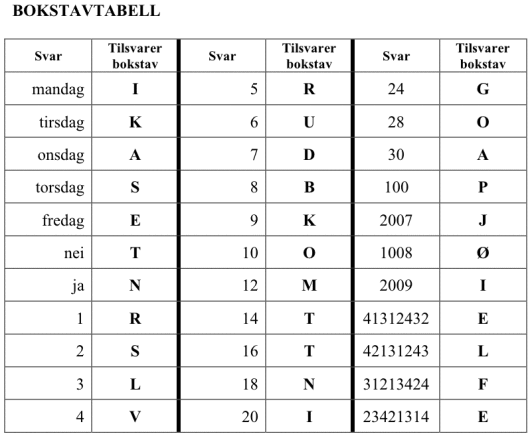
Årets julekalender for 5.-7. trinn består av 9 enkeltstående oppgaver som kan løses uavhengig av hverandre. Alle oppgavene gir et tall som svar, og dette tallet tilsvarer en bokstav som dere finner i bokstavtabellen sist i oppgavesettet. Oppgave 2 gir to tallsvar og begge har sin egen bokstav. Det vil si at dere skal finne 10 bokstaver totalt.
Når dere har alle 10 bokstavene skal disse settes sammen til et norsk ord, og det er dette ordet som er løsningen på årets julekelender for 5.-7. trinn. Oppgavene er nummerert, men rekkefølgen har ingenting å si, bokstavene må uansett stokkes om. Stikkord for årets løsning er noe vi gjør i geometri.
Klasser som ønsker å delta i konkurransen om å vinne premier må sende inn løsningene i en e-post til 5-7trinn-jul2008@matematikk.org innen 9. januar 2009.
Innholdet i e-posten må være:
Løsningsord
Klasse(r):
Antall elever som har deltatt:
Kontaktpersons e-postadresse:
Skole:
Skolens postadresse:
Innsendingsfrist for konkurransen er 9. januar 2009.
Vinnerne offentliggjøres via startsiden, www.matematikk.org tirsdag 13. januar kl. 12.00.
Spørsmål kan sendes til post@matematikk.org.
Lykke til med oppgavene, og god jul!
Oppgavene er laget av matematikk.org
Elevens oppgaveark
Alle oppgavene gir et tall som svar, og dette tallet tilsvarer en bokstav som dere finner i bokstavtabellen sist i oppgavesettet. Oppgave 2 gir to tallsvar og begge har sin egen bokstav. Det vil si at dere skal finne 10 bokstaver totalt.
Når dere har alle 10 bokstavene skal disse settes sammen til et norsk ord, og det er dette ordet som er løsningen på årets julekelender for 5.-7. trinn. Oppgavene er nummerert, men rekkefølgen har ingenting å si, bokstavene må uansett stokkes om. Stikkord for årets løsning er noe vi gjør i geometri.
Oppgave 1
Ta en blå kube og lim på 6 nye, like store, blå kuber på den første.
Så tar du gule kuber, like store som de blå, og limer på alle de ledige, blå flatene. Hvor mange gule kuber trenger du for å dekke de tilgjengelige blå overflatene?
Oppgave 2
Et åttesifret tall inneholder to ett-tall, to to-tall, to tre-tall og to fire-tall. Det er et siffer mellom ett-tallene, to siffer mellom to-tallene, tre siffer mellom tre-tallene og 4 siffer mellom fire-tallene. Hvilke tall blir dette?
Oppgave 3
Anne: Jeg kan telle til 1 million.
Per: Det kan jeg også, men kan du telle til en million på en dag?
Anne: Det tar vel ikke så lang tid? klart jeg kan det!
Tror du Anne klarer å telle alle tallene fra 1 til 1 million i løpet av en dag, JA eller NEI?
Oppgave 4
Snille tall er tosifrede tall som blir seg selv dersom vi tar produktet av sifrene og legger til summen av dem. Hvor mange snille tall finnes det?
Tallet 45 er ikke et snilt tall, fordi 45 gir 4·5 + (4+5) = 29.
Tallet 19 er et snilt tall, fordi 19 gir 1·9 + (1+9) = 19 .
Oppgave 5
Du får vite at 30 elever har 25 forskjellige fødselsdager seg i mellom. Hva er det største antallet elever som kan ha den samme fødselsdagen?
Oppgave 6
Skolen har show for foreldrene, og i en ringdans hvor elevene står like langt fra hverandre langs en sirkel står elev nummer 6 rett overfor elev nummer 20. Hvor mange elever er med på ringdansen?
Oppgave 7
Av og til er det godt med godt! Jeg hadde 17 kroner i lomma og ville kjøpe godterier for alle pengene. I kiosken hadde de bare godterier til 3 kroner og 4 kroner stykket. Hvor mange godterier fikk jeg kjøpt for de 17 kronene mine?
Oppgave 8
| 6 | 7 | 29 | 4 | 13 | 5 | 2 | 8 | 9 |
Hvilket tall står igjen etter at vi har gjort følgende;
Ta først vekk to tall som har sum 12 og differanse 2, ta så vekk to tall som har sum 12 og produkt 32. Etter dette fjerner du de to tallene som har en differanse på 7 og et produkt på 78, og til slutt tar du vekk to tall som er slik at når du deler det første med det andre blir kvotienten 3 og resten 2.
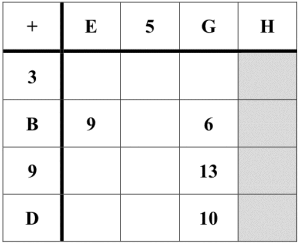
Oppgave 9
Fyll ut addisjonstabellen under (f.eks er B+G=6). Hvilket tall må H være dersom summen av alle tallene i den markerte kolonnen er 24?