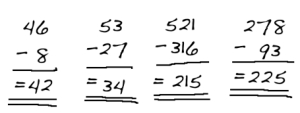Julekalender 2011, 5.-7. trinn
Lærerens instruksjoner
ALT DU FINNER PÅ DISSE NETTSIDENE KAN DU LASTE NED I ET UTSKRIFTSVENNLIG FORMAT (pdf), se vedlegget i høyrespalten.
Årets julekalender for 5.-7. trinn består av 9 enkeltstående oppgaver som kan løses uavhengig av hverandre. Oppgavene 4, 6, 8 og 9 er delt i to nivåer slik at du som lærer, eller eleven selv, kan velge hvilket nivå som passer best. Nivå 1 er det letteste. Alle oppgavene gir et tall som svar, og dette tallet tilsvarer en bokstav som dere finner ved å velge rett svaralternativ.
Når dere har alle 9 bokstavene skal disse settes sammen til et norsk ord, og det er dette ordet som er løsningen på julekalenderen for 5.-7. trinn. Oppgavene er nummerert, men rekkefølgen har ingenting å si, for bokstavene må uansett stokkes.
Klasser som ønsker å konkurrere om å vinne premier må sende inn løsningen i en e-post til julekalender5-7@matematikk.org innen fredag 6. januar 2012. Det er læreren som på vegne av trinnet/gruppen skal sende inn løsningsordet.
Innholdet i e-posten skal være:
LØSNINGSORDET
Klasse(r):
Antall elever som har deltatt:
Kontaktpersons e-postadresse:
Skole:
Skolens postadresse:
Innsendingsfrist for konkurransen er 6. januar 2012.
Vinnerne offentliggjøres via startside www.matematikk.org 10. januar kl. 12.00.
Spørsmål kan sendes til post@matematikk.org.
Lykke til med oppgavene, og god jul!
Elevens oppgaveark
Eksempler på årets oppgaver for 5. - 7. trinn
Oppgave 2
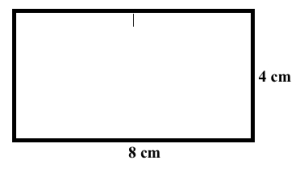
Tenk deg at du har 3 rektangler som alle har lengde 8 cm og bredde 4 cm.
På hvor mange forskjellige måter kan du lage nye, store rektangler når du må bruke alle rektanglene hver gang.
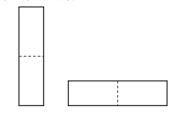
Rotasjon eller speiling av et rektangel teller ikke som en ny måte. De to rektanglene nedenfor teller derfor bare som en måte.
Oppgave 8
Barnebarnet til bestemor Andersen har lært å sette opp minusstykker over hverandre. Det er barnebarnet til bestemor Andersen som har satt opp og regnet de fire stykkene du ser her, men alle svarene er gale!
Gjør barnebarnet til bestemor Andersen én og samme feil i alle regnestykkene?