Fibonaccitallene
Tallfølgen 1,1,2,3,5,8,13,... er bygd opp ved at hvert tall i følgen er summen av de to foregående tallene i følgen. Tallene i denne følgen kalles fibonaccitallene, og de dukker opp på de merkeligste steder...
Opphavet til disse tallene er et problem som Fibonacci jobbet med i år 1202. Problemet handlet om hvor fort kaniner kan formere seg under ideelle forhold:
Anta at et nyfødt par kaniner, en hann og en hunn, puttes i en innhegning.
Kaniner parer seg når de er en måned gamle, og etter to måneder kan en hunn føde et nytt par kaniner. Anta nå at våre kaniner ikke dør og at hunnene alltid føder et nytt par, en hann og en hunn, hver måned fra sin andre leve-måned.
Fibonaccis spørsmål var: Hvor mange par kaniner er det i innhegningen etter ett år?
Løsning:
Vi starter med 1 par (par nr. 1).
Etter 1 måned: Par nr. 1 parrer seg, men vi har fortsatt bare 1 par.
Etter 2 måneder: Hunnen i par nr. 1 føder et nytt par, par nr. 2, så nå har vi 2 par kaniner.
Etter 3 måneder: Par nr. 1 føder sitt andre par, par nr. 3, mens par nr. 2 parrer seg, så dermed har vi 3 par i innhegningen.
Etter 4 måneder: Den første hunnen føder sitt tredje par, par nr. 4. Par nr. 2 får sitt første par, par nr. 5, og par nr. 3 parrer seg. Totalt har vi nå 5 par.
Etter 5 måneder: Par nr. 1, 2 og 3 får ett nytt par hver og par nr. 4 og 5 parrer seg. Totalt 8 par.
Generelt vil vi etter hver måned ha alle parene fra forrige måned pluss noen nye par. De nye parene er ett par fra hvert av parene vi hadde to måneder tilbake (de nye parene vi fikk forrige måned får ikke avkom før neste måned). For å finne ut hvor mange par vi har i slutten av en måned, må vi altså plusse sammen antall par vi hadde på slutten av de to foregående månedene. Dette gir tallfølgen
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
der leddene vil gi oss totalt antall par i innhegningen på slutten av hver måned. Svaret på Fibonaccis spørsmål er dermed 233 par kaniner.
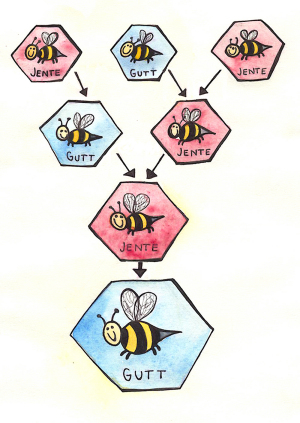
Fire generasjoner honningbier. (Illustrasjon: Birte Lohne Løvdal)
Kaninoppgaven er kanskje ikke så realistisk, men i naturen fins det mange eksempler der fibonaccitallene modellerer situasjonen vi ser på.
Et eksempel er honningbier. Hann-honningbier produseres fra dronningbiens ubefruktede egg, så hannene har bare en mor og ingen far. Hunn-biene har både mor og far. Hvis vi dermed teller forfedrene til en hann-honningbie i hver generasjon får vi:
Start: 1 hann-honningbie
En generasjon tilbake: 1 mor
To generasjoner tilbake: 2 besteforeldre (morens foreldre)
Tre generasjoner tilbake: 3 oldeforeldre (bestemors foreldre og bestefarens mor)
Fire generasjoner tilbake: 5 tippoldeforeldre (2 oldemødres foreldre og oldefars mor)
osv.
For hver generasjon har vi altså to typer forfedre; de kvinnelige som har to foreldre, og altså "deler seg i to", og de mannlige som kun har en mor, og således ikke forgrener seg. Den slags oppførsel modelleres nettopp av fibonaccitallene.
Denne typen oppførsel kan vi også finne på ulike blomster, ved å se hvordan stilken forgrener seg: Begynn ved bakken og følg stilken oppover.
Hvis vi trekker nogenlunde rette horisontale streker mellom delingspunktene (der stilken forgrener seg), som er ca. i samme høyde, vil svært ofte antall grener mellom disse strekene være fibonaccitall. Nyserylliken er et slikt eksempel:
Nyseryllik
Vi nevner noen flere eksempler på fibonaccitallenes opptreden i naturen:
- Hvis vi teller antall kronblader (blomsterblader) på en blomst, er det i mange tilfeller et fibonaccitall. For eksempel har smørblomster 5 kronblad, liljer 3, gullkrager 13, tusenfryd kan ha 34 eller 55 og blomster i kurvplantefamilien (slik som hestehov og løvetann) kan ha 89 blomsterblader.
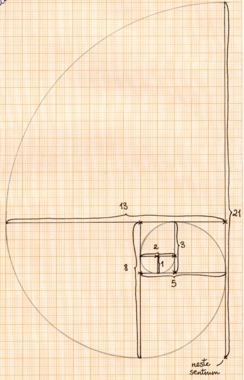
- Fibonaccispiralen er spiralen som er satt sammen av sirkelbuer der radiene er et nytt fibonaccitall for hver 90. grad (kvart rotasjon). Det vil si at vi tegner en spiral der vi starter med en halvsirkel med radius 1, deretter en kvart sirkelbue med radius 2 etterfulgt av en kvart bue med radius 3 og så videre.
Fibonaccispiralen. Du kjenner den kanskje igjen fra sneglehus og diverse skjell? - En annen type spiraler er såkalte "botaniske spiraler". Hvis du ser nærmere på for eksempel kongler, ananas eller frøhodene i en solsikkeblomst, vil du finne mange spiraler. Det er påvist en klar sammenheng mellom slike spiraler og fibonaccitallene. Hvis du for eksempel teller antall spiraler i solsikkeblomsten vil du finne 21 spiraler som går med klokka og 34 som går mot! Generelt vil antall botaniske spiraler med og mot klokka nesten alltid være nabo-fibonaccitall. Studier har vist at dette er det mest hensiktsmessige pakkemønsteret en plante kan benytte seg av.
La oss nå se litt nærmere på noen av alle de matematiske egenskapene til fibonaccitallene. Dem er det nemlig mange av. Det er også mange som har studert fibonaccitallene, og noen har funnet følgende mønster blant disse tallene: Hvis vi ser på det siste sifferet i hvert fibonaccitall, får vi følgen
0,1,1,2,3,5,8,3,1,4,5,.....
(Det er mange som bruker 0 som det første fibonaccitallet.) Det viser seg at når vi kommer til det 60. tallet i denne følgen av siste sifre, starter den på nytt, og repeteres for hvert 60. tall. Vi sier at det siste sifferet i fibonaccitallene har en sykel av lengde 60. Ser vi på de to siste sifrene (00,01,01,02,03,05,08,13,....), har vi en sykel av lengde 300. For de tre siste sifrene har vi en sykel av lengde 1 500, for fire 15 000, for fem 150 000 osv. Det ser ut til å være et mønster blant mønstrene i fibonaccitallene...
Vi innfører fra nå notasjonen F(n) for det n-te fibonaccitallet, for eksempel er F(3) = 2 og F(7) = 13.
Hvis vi starter med F(3), så ser vi at hvert 3. fibonaccitall (F(3), F(6), F(9)...) er et multippel av F(3).
Siden F(3) = 2 vil det si at disse tallene er partall. Hvis vi starter på F(4), så er hvert 4. fibonaccitall (F(4), F(8), F(12)...) et multippel av F(4) = 3. Starter vi med F(5) så er hvert 5. fibonaccitall et multippel av F(5) = 5. Vi har observert et mønster og gjetter nå at F(nk) er et multippel av F(k) for alle verdier av n og k=1,2,...
Siden dette er et resultat som gjelder for de naturlige tallene, kan vi prøve å bevise dette ved induksjon. Det klarer vi (Selv om vi ikke gjør det her), og dermed er gjetningen vår blitt et resultat.
Vi har også et annet resultat som omhandler faktoriseringen av fibonaccitallene. Det kalles Carmichaels teorem: Bortsett fra fire unntak har vi at hvis vi ser på primtallsfaktorene til et fibonaccitall vil det være minst en av dem som ikke har forekommet som en faktor i et mindre fibonaccitall. Unntakene er F(1) = 1, F(2) = 1, F(6) = 8, F(12) = 144 (de to første har ingen primtallsfaktorer, og og både 2 og 3 er faktorer i mindre fibonaccitall).
En annen kuriositet om primtall og fibonaccitall er at hvis vi ser på de naturlige tallene som kommer før og etter et fibonaccitall er disse aldri primtall. Dette gjelder for alle fibonaccitall større enn 8 (for 8 er naboene 7 og 9, og 7 er et primtall). Å lete etter primtall er "big business" i dag. I letingen kan vi iallfall utelukke naboene til fibonaccitallene.
Vi har nevnt mønstre som opptrer når vi ser på de siste sifrene i fibonaccitallene, så vi spør nå: Er det noen mønstre i de første sifrene i fibonaccitallene? Hva er sannsynligheten for at et fibonaccitall begynner med sifferet 1? Hva med 4? Det viser seg at første siffer i fibonaccitallene oppfører seg ganske likt som for eksempel første siffer i antall innbyggere i verdens land: Det mest "populære" sifferet i begge tilfeller er 1, deretter følger 2, helt ned til 9, som er det sifferet som dukker opp færrest ganger som første siffer. Det er faktisk ca. en tredjedel av verdens land som har et antall innbyggere der første siffer er 1. Dette er eksempler på samlinger av tall som følger Benfords lov.
Vi sier at en samling tall følger Benfords lov hvis første sifferet i tallene følger følgende distribusjon:
| Siffer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Prosentandel | 30 | 18 | 13 | 10 | 8 | 7 | 6 | 5 | 5 |
Denne loven opptrer ofte i statistikken, nemlig når vi har en samling tall som føger en potenslov, dvs. at tallene forholder seg til en potens av et tall. Se for eksempel på tallene som er en potens av 2: 2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072,262144,524288,...
Det er 1 som opptrer oftest som første siffer, deretter følger 2 osv.
Når vi kaster en terning eller trekker et Lotto-tall er henholdsvis tallene 1-6 og 1-34 like sannsynlige. Her gjelder ingen potenslov. Men i tilfeller som fibonaccitallene, antall innbyggere i verdens byer eller land, størrelsene på verdens innsjøer og prisene på aksjer på børsen har vi en potenslov. Fibonaccitallene forholder seg for eksempel til potenser av tallet "det gylne snitt" som ofte betegnes (uttales "fi", skrives "phi").
Tanken om "Det gylne snitt" går tilbake til Pytagoras' tid, da man så på enkelte proporsjoner og forhold som penere enn andre. Tenk deg at vi har en størrelse som deles i to slik at den største delen forholder seg til den minste slik hele størrelsen forholder seg til den største delen. Da sier vi at størrelsen er delt etter det gylne snitt. La oss se hva forholdet, det gylne snitt, blir.
Vi kaller de to delene A og B. Hvis A er den største delen, skal vi altså finne forholdet . Vi har som gir oss ligningen . Siden B≠ 0 kan vi dele på B2 som gir andregradsligningen . Løsningene av denne gir
eller .
Dette gir forholdet siden vi vil ha et positivt tall. Det er tilnærmet lik 1,61803.
Så var det sammenhengen mellom fibonaccitallene og det gylne snitt: I utregningen av det gylne snitt hadde vi løsningene og for andregradsligningen vår. For fibonaccitallene viser det seg at vi har formelen .
La oss se hvordan vi kan få frem fibonaccitallene ved å manipulere andregradsligningen . passer inn i denne ligningen, det vil si at . Hvis vi multipliserer ligningen med høyere og høyere potenser av og erstatter med får vi:
.
.
.
.
Vi gjetter at
,
noe vi kan vise at stemmer ved induksjon.
Nå brukte vi , men passer også inn i andregradsligningen, så dermed får vi på tilsvarende måte .
Ser vi på differansen , får vi formelen vi ga over for F(n).
Hvis vi ser på forholdet for stadig større n, får vi dermed etter en del mellomregning at
Siden , blir det andre leddet både over og under brøkstreken mindre og mindre for stadig større n, så blir nærmere og nærmere , det gylne snitt. For eksempel er
55/34 ~ 1,61765
89/55 ~ 1,61818
144/89 ~ 1,61798
233/144 ~ 1,61806.
La oss nå manipulere nok et polynom. Denne gangen ser vi på polynomet P(x) som har fibonaccitallene som koeffisienter:
Når vi setter inn x-verdier for x < 1, vil vi få en sum, og siden koeffisientene er fibonaccitall kan vi regne ut hva summen blir:
Se på polynomene
og
Hvis vi nå tar polynomet , vil vi kun få igjen polynomet 1, siden alle andre ledd kanselleres (det er slik fibonaccitallene er bygd opp - prøv selv!). Dermed får vi at . Hvis vi setter inn , ser vi på . Dette gir oss følgende tall skrevet i titallssystemet: 1,12359550561.... (9-tallet kommer fra ). Vi kan nå finne den nøyaktige brøken for dette desimaltallet, nemlig ved å sette inn i P(x) dvs. .
Fibonaccitallene dukker også opp i Pascals trekant. Pascals trekant er rader med tall som danner en trekant. Trekanten er bygd opp med 1-ere på kantene og der hvert tall innenfor disse er summen av de to tallene i raden over som er på hver side av tallet:
| 1 | ||||||||||||
| 1 | 1 | |||||||||||
| 1 | 2 | 1 | ||||||||||
| 1 | 3 | 3 | 1 | |||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 |
... og så videre.
Hvis vi nå tegner Pascals trekant slik at alle radene flyttes til høyre slik at vi får en diagonal med 1-ere, kan vi summere kolonnene. Gjett hva disse summene blir... Vi setter det i en tabell:
| 1 | ||||||||||
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | ... | |||||
| 1 | 6 | 15 | 20 | ... | ||||||
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... |
Vi kan prøve å forklare dette ved å se på antall mulige måter å summere tallene 1 og 2 på slik at summen blir n, n et naturlig tall. For eksempel hvis n=4, får vi 1+1+1+1,2+1+1,1+2+1,1+1+2 og 2+2, som gir 5 måter. Hvis vi i tillegg deler måtene opp etter hvor mange 1-ere og 2-ere vi bruker, får vi delt opp n som i n-te kolonne av Pascals trekant (der vi har flyttet radene som over). Så for eksempel, 5 deles i 1 3 1.
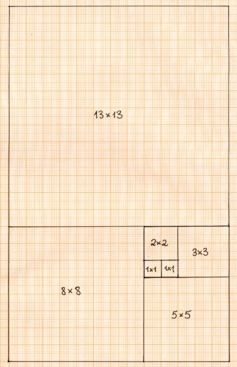
Til slutt tar vi en liten tur tilbake til fibonaccispiralen. På tilsvarende måte som vi lagde denne spiralen ved å pusle sammen sirkelbuer der radiene var fibonaccitall, kan vi pusle sammen kvadrater der sidene er fibonaccitall og få rektangler:
Kvadrater der sidelengdene er Fibonaccitall.
Når vi bygger et nytt rektangel ved å legge til et kvadrat, blir den korte siden i rektangelet lik den lengste siden i det forrige rektangelet, og den lange siden blir summen av sidene i de to siste kvadratene vi la til.
Vi har altså et puslespill av kvadrater som har lengder som er et fibonaccitall.
Hva forteller dette puslespillet oss matematisk? Hvis vi ser på arealene vi får, får vi
Generelt ser det altså ut til at hvis vi summerer kvadratene av fibonaccitall vil summen bli lik produktet av det største fibonaccitallet vi brukte i kvadratene og det neste fibonaccitallet. Sagt matematisk, 12+12+22+32+52+82+...+F(n)2=F(n)F(n+1), noe som igjen kan vises ved induksjon.
Del på Facebook