Udempet og dempet svinging

Anta at vi har et lodd med masse $m$ som henger vertikalt i en fjær. Vi skal nå se hvordan vi kan beskrive posisjonen $y$ til loddet med hensyn til tid ved hjelp av differensiallikninger av andre orden. Vi kaller posisjonen til loddet når det henger i ro for likevektspunktet, og vi setter $y=0$ når loddet er her.

Om vi prøver å presse loddet oppover eller dra det nedover, er kraften $F_1$ vi bruker proposjonal med posisjonen til loddet. Fjæret vil gjøre mer motstand jo lenger vekk fra likevektspunktet vi flytter loddet. Dermed er $F_1=ky$ for en konstant $k$. Vi kaller konstanten $k$ for fjærkonstanten.

Om vi holder loddet i ro kommer fjæret til å virke med en kraft $F_2$ som er like stor som kraften vi bruker på loddet, men virker i motsatt retning: $$F_1+F_2=0.$$ Da $F_1=ky$ har vi at $$F_2=-ky.$$

Om vi slipper loddet (og ignorerer friksjon) forsvinner kraften $F_1$ vi brukte på loddet, og vi står kun igjen med kraften $F_2$. Newton’s andre lov forteller oss at $F_2=ma$, hvor $a$ er akselerasjonen til loddet. Dermed er $$ma=-ky.$$ Men vi vet at akselerasjonen er den dobbeltderiverte til posisjonen med hensyn til tid, det vil si at $$my″+ky=0.$$ Vi har beskrevet følgende:

Eksempel 1

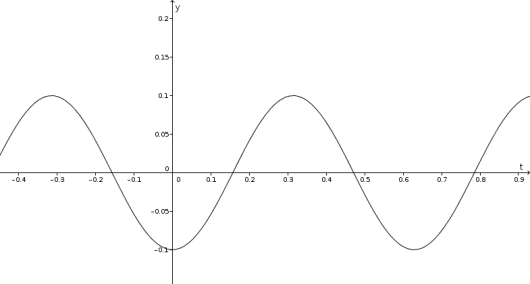
Anta at vi har et lodd på $0,3$ kilogram som henger i en fjær med fjærkontant på $30$ Newton per meter. Vi drar loddet ned $0,10$ meter og slipper det. Formelen for udempet svingning forteller oss at posisjonen til loddet er gitt ved differensiallikningen $$0,3y″+30y=0.$$ Den karakteristiske likningen er gitt ved $$0,3r^2+30=0$$ og har løsninger $r=\pm 10\sqrt{-1}$. Da er den generelle løsningen gitt ved $$y=C_1\sin 10t+C_2\cos 10t.$$ Vi vet at ved $t=0$ så er $y\left(0\right)=-0,10$, dermed er $$y\left(0\right)=C_2=-0,10.$$ Merk at vi også har en initialbetingelse på $y\prime$: i øyeblikket vi slipper loddet, ved $t=0$, så er farten $y\prime =0$. Ved kjerneregelen har vi at $$y\prime =10C_1\cos 10t-10C_2\sin 10t.$$ Setter vi inn $t=0$ får vi $$10C_1=0$$ som gir at $C_1=0$. Dermed er løsningen gitt ved $$y=-0,10\cos 10t.$$

Om vi tegner grafen til funksjonen i eksempelet ovenfor, får vi følgende:

Grafen beskriver posisjonen til loddet med hensyn til tid. Vi ser at grafen er periodisk, og loddet kommer like langt over og under likevektspunktet hver periode. Dette ville aldri ha skjedd i virkeligheten, hvor loddet vil svinge om likevektspunktet med stadig mindre amplitude. I praksis kommer det vil å virke enda en kraft på loddet: friksjonskraften som vi til nå har ignorert. Når farten blir større vil også friksjonskraften bli større, og dermed er friksjonskraften $F_3$ proposjonal med farten til loddet: $F_3=-k_{1}y\prime$ hvor $k_1$ er en konstant, friksjonstallet. Her har vi et negativt fortegn siden kraften vil virke i motsatt retning av farten. Om vi drar loddet nedover eller skyver det oppover for så å slippe det, har vi da at $$F_2+F_3=-k_{2}y-k_{1}y\prime$$ hvor $k_2$ er fjærkonstanten og $F_2=-k_{2}y$ som tidligere. Om vi igjen bruker Newton’s andre lov har vi at $F_2+F_3=my″$ hvor $m$ er massen til loddet, og vi får at $$my″=-k_{2}y-k_{1}y\prime$$ eller $$my″+k_{1}y\prime +k_{2}y=0.$$ Vi har beskrevet følgende:

Eksempel 2

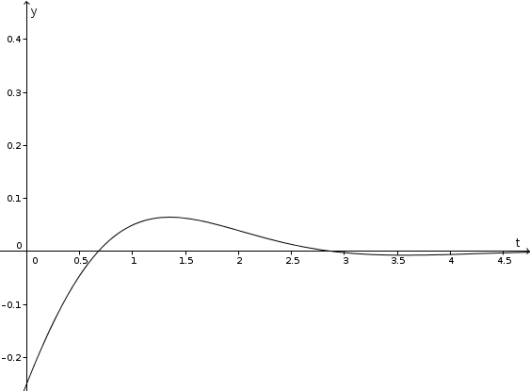
Gitt en lodd med masse $0,1$ kilogram hengende i en fjær med fjærkonstant $0,3$ Newton per meter og friksjonstall $0,2$ Newtonsekunder per meter som vi trekker ned $0.25$ meter for så å slippe det, får vi differensiallikningen $$0,1y″+0,2y\prime +0,3y=0.$$ Den karakteristiske likningen $$0,1r^2+0,2r+0,3=0$$ har løsninger $r_1=-1+\sqrt{2}\sqrt{-1}$ og $r_2=-1-\sqrt{2}\sqrt{-1}$. Da vet vi at den generelle løsningen er gitt ved $$y=e^{-t}\left(C_1\sin \right(\sqrt{2}t)+C_2\cos (\sqrt{2}t\left)\right).$$ Vi vet at $y\left(0\right)=-0,25$, slik at $$y\left(0\right)=C_2=-0,25.$$ Da er $$y=e^{-t}\left(C_1\sin \right(\sqrt{2}t)-0,25\cos (\sqrt{2}t\left)\right).$$ I øyeblikket vi slipper loddet kommer farten vil å være null: $y\prime \left(0\right)=0$. Om vi deriverer funksjonen ved hjelp av produktregelen og kjerneregelen får vi at

$y\prime =-e^{-t}\left(C_1\sin \right(\sqrt{2}t)-0,25\cos (\sqrt{2}t\left)\right)+$

$$e^{-t}\left(\sqrt{2}{C}_1\cos \right(\sqrt{2}t)+(0,25\left)\sqrt{2}\sin \right(\sqrt{2}t\left)\right).$$ Setter vi inn for $t=0$ får vi at $$-0,25+\sqrt{2}{C}_1=0.$$ Løser vi for $C_1$ har vi at $C_1=\frac{1}{4\sqrt{2}}$. Dermed har vi funnet løsningen $$y=e^{-t}\left(\frac{1}{4\sqrt{2}}\sin \right(\sqrt{2}t)-0,25\cos (\sqrt{2}t\left)\right).$$ Om vi nå tegner grafen til funksjonen får vi et mer realistisk bilde:

Vi ser at loddet nærmer seg likevektspunktet veldig raskt. Det er selvsagt også mulig å få dempede svingninger med amplitude som er større i starten og synker saktere: vi oppfordrer leseren til å prøve seg med forskjellige konstanter for så å tegne grafen til løsningen med digitale hjelpemidler.