Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3024 2015 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 9 oppgaver. Del 2 har 4 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.:
- London Eye, en.wikipedia.org, www.saylor.org (01.12.2014)
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4DNB
Deriver funksjonene
a)
b)
c)
Oppgave 2 (5 poeng) Nettkode: E-4DNF
Regn ut integralene
a)
b)
c)
Oppgave 3 (4 poeng) Nettkode: E-4DNJ
a)
Bruk en integrasjonsmetode til å vise at
b)
Løs differensiallikningen
Oppgave 4 (3 poeng) Nettkode: E-4DNS
En uendelig geometrisk rekke er gitt ved
a)
Bestem konvergensområdet til rekken.
b)
Bestem slik at
Oppgave 5 (6 poeng) Nettkode: E-4DO2
Punktene , og er gitt.
a)
Bestem . Bestem arealet av .
b)
Punktene , og ligger i et plan . Bestem likningen for planet .
c)
En partikkel starter i origo . Etter tiden er partikkelen i et punkt gitt ved
Hvor lang tid tar det før partikkelen treffer planet ? Bestem koordinatene til punktet der partikkelen treffer .
Oppgave 6 (2 poeng) Nettkode: E-4DO7
En tallfølge er gitt ved at og
Bruk induksjon til å bevise at
Oppgave 7 (6 poeng) Nettkode: E-4DRB
Funksjonen er gitt ved
a)
Bestem nullpunktene til ved regning.
b)
Bruk til å bestemme -verdien til eventuelle topp- eller bunnpunkter på grafen til .
c)
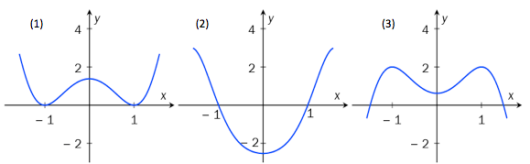
Nedenfor er det tegnet tre grafer. Én av dem er grafen til . Avgjør hvilken.
Begrunn svaret.
Oppgave 8 (4 poeng) Nettkode: E-4DRF
En trigonometrisk formel er gitt ved
a)
Bruk formelen til å bestemme et uttrykk for .
b)
Skriv uttrykket så enkelt som mulig.
Oppgave 9 (2 poeng) Nettkode: E-4DRI
Løs likningen
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4DRK
Roger planlegger en sykkeltur. Han regner med å kunne starte med farten 26 km/h. Etter hvert vil farten avta etter formelen
- og er begge funksjoner som er avhengige av tiden målt i timer
- er farten målt i kilometer per time
- er den tilbakelagte veilengden målt i kilometer
a)
Bestem farten etter 125 km.
b)
Formelen ovenfor kan vi skrive som differensiallikningen
Bestem når .
c)
Hvor langt sykler Roger den første timen? Hvor lang tid bruker han på 125 km?
Oppgave 2 (6 poeng) Nettkode: E-4DRO
Hjørnene i en pyramide er , , og .
a)
Bestem et uttrykk for volumet av pyramiden.
b)
Bestem koordinatene til slik at .
c)
Bestem koordinatene til slik at volumet blir minst mulig.
Oppgave 3 (6 poeng) Nettkode: E-4DRT
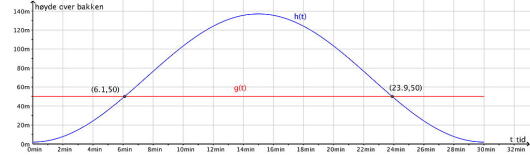
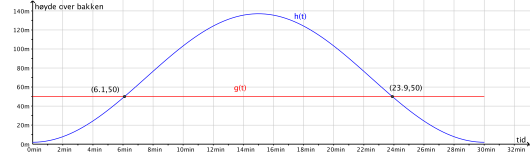
London Eye er et pariserhjul med diameter lik 135 m. En runde tar 30 min. Passasjerene går ombord i pariserhjulet fra en plattform som ligger 2 m over bakkenivå.
Etter min fra ombordstigning er en passasjer m over bakkenivå. Det kan vises at
a)
Bruk graftegner til å tegne grafen til for . Bestem grafisk når passasjeren er 50 m over bakkenivå.
b)
Bestem vendepunktene på grafen til .
Forklar hvilken praktisk informasjon verdiene av og gir.
Oppgave 4 (6 poeng) Nettkode: E-4DS9
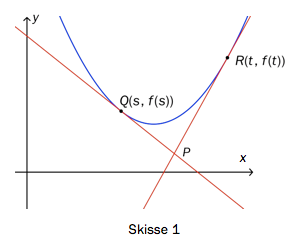
Funksjonen er gitt ved
Tangentene i punktene og skjærer hverandre i et punkt .
Se skisse 1.
a)
Vis at likningene for de to tangentene er
og
b)
Bruk CAS til å vise at -koordinaten til punktet er gitt ved .
c)
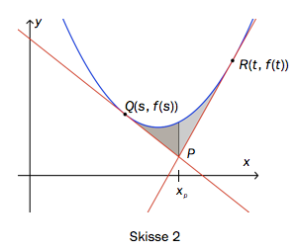
Den vertikale linjen deler området mellom grafen og tangentene i to områder.
Se skisse 2.
Bruk CAS til å vise at arealene av de to områdene er like store for alle verdier av og .