
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3024 2015 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 9 oppgaver. Del 2 har 5 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- kriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.:
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4DHY
Deriver funksjonene
a)
Løsningsforslag a)
Jeg tenker
Funksjonen er en konstant multiplisert med en cosinusfunksjon med kjerne lik . Derfor vil det være hensiktmessig å bruke kjerneregelen for derivasjon. Kjerneregelen for derivasjon sier at.
Ved å sette og huske at den deriverte av er , kan vi finne
Svar:
Mer om
Denne oppgaven er om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av trigonometriske funksjoner.
b)
Løsningsforslag b)
Jeg tenker
Funksjonen er et produkt av to funksjoner, og , som vi klarer å derivere hver for seg. Derfor er det hensiktsmessig å bruke produktregelen for derivasjon.
Produktregelen for derivasjon sier atDet betyr at hvis vi setter og så må
Svar:
Mer om
Denne oppgaven er om
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere forklaringer og eksempler se artikkelen Å derivere sammensatte uttrykk.
Visste du at
Dersom du i denne oppgaven (gjelder kun for )hadde glemt produktregelen for derivasjon, men tilfeldigvis husket brøkregelenkunne vi løst oppgaven på følgende måte. Siden må ogsåog siden den deriverte av er må vi derfor også haDenne likningen kan vi løse for slik at vi sitter igjen medog siden følger det atsom er det vi viste i denne oppgaven.
c)
Løsningsforslag c)
Jeg tenker at
Funksjonen er et produkt av to funksjoner, og , som er lettere å derivere hver for seg. Derfor kan det være lurt å benytte produktregelen for derivasjon.
Ifølge produktregelen, som sier at , finner viVed å benytte kjerneregelen med kjerne kan vi videre skriveHvis vi nå bruker kjerneregelen med kjernen finner viDette betyr at
Svar:
Mer om
Denne oppgaven er om En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. Cosinus er en trigonometrisk funksjon. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Eksponentialfunksjon

Sinus
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Derivasjon
For flere forklaringer og eksempler på derivasjon, se artikkelen Kjerneregelen.
Oppgave 2 (4 poeng) Nettkode: E-4DIW
Bestem integralene
a)
Løsningsforslag a)
Jeg tenker
Vi må integrere funksjonen fra til . Det kan vi gjøre ved å benytte det vi vet om den deriverte av ledd på formen og at integralet av en sum er lik summen av integralene.
Siden integralet av en sum er lik summen av integralene kan vi skriveSiden den deriverte av er , av er og av er må vi ha
Alternativ løsning
Ved å gjenkjenne første kvadratsetning kan vi skriveog ved å bruke substitusjonsmetoden med substitusjonen finner viVed å komme på at den deriverte av er finner vi altså
Svar:
Mer om
Denne oppgaven er om
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Andre kvadratsetning
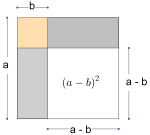
Andre kvadratsetning sier at
.
For flere forklaringer og eksempler på integrasjon, se artikklen Bestemte integraler.
b)
Løsningsforslag b)
Jeg tenker
Vi må finne en funksjon som blir lik når den deriveres. Siden den deriverte av er kan det være hensiktsmessig å forsøke metoden for ”baklengs kjerneregel”, nemlig substitusjonsmetoden.
Ved å benytte metoden for integrasjon ved substitusjon, med substitusjonen , kan vi skriveSiden den deriverte av er finner vi Ved nå å sette inn for får viVi har altså funnet at
Svar:
Mer om
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null. Brøk kan sees som et tall på tallinja eller som del av en mengde. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Integrasjon
Brøk

Eksponentialfunksjon

Derivasjon
For flere forklaringer og eksempler på integrasjon, se artikklen Integrasjon ved substitusjon.
Oppgave 3 (3 poeng) Nettkode: E-4DJV
Funksjonen er gitt ved
Vi roterer grafen til om -aksen.
Vis at volumet av omdreiningslegemet blir
Løsningsforslag
Jeg tenker
Ved å dele opp omdreiningslegemet til i uendelig mange, uendelig tynne sylindere med radius og tykkelse kan vi uttrykke volumet av omdreiningslegemet som et integral.
Ved å dele opp omdreiningslegemet til i uendelig mange, uendelig tynne sylindere med med radius og tykkelse , og derfor volum , kan vi skrive volumet av omdreiningslegemet som integraletSiden den deriverte av er finner vi atsom er det vi ønsket å vise.
Mer om
Denne oppgaven er om
Omdreiningslegeme
Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.
Oppgave 4 (4 poeng) Nettkode: E-4DK5
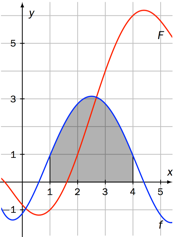
Figuren viser grafene til funksjonene og .
Det er gitt at
a)
Bruk figuren til å bestemme .
Løsningsforslag a)
Jeg tenker
Siden må vi finne verdien til i punktet .
På figuren ser det ut til at grafen til har en høyde på omlag når . Det betyr at
Svar:
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.
b)
Bruk figuren til å bestemme arealet av det markerte flatestykket.
Løsningsforslag b)
Jeg tenker
Siden kan vi se på som en løsning av integralet .
Siden betyr atmå arealet avgrenset av , -aksen og -verdiene og være gitt somPå figuren ser ut til å ta verdien i og i . Det betyr at
Svar:
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.Graf
Integrasjon
Areal
Noen måleenheter for areal er m2, dm2 og cm2.
For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.
Oppgave 5 (5 poeng) Nettkode: E-4DK8
En kuleflate er gitt ved likningen
a)
Vis at punktet ligger på kuleflaten.
Løsningsforslag a)
Jeg tenker
Punktet ligger på kuleflaten hvis, og bare hvis, koordinatene til tilfredsstiller likningen for kuleflaten.
Punktet ligger på kuleflaten hvis likningenstemmer for . Sidenligger altså på kuleflaten.
Svar: ligger på kuleflaten.
Mer om
Denne oppgaven er om
Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
Kule
Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.
b)
Bestem sentrum og radius til kulen.
Løsningsforslag b)
Jeg tenker
Dersom vi klarer å skrive likningen for kuleflaten på formen følger det at kulen har radius og sentrum i .
Ved å samle alle leddene som inneholder i likningen for kuleflaten til et fullstendig kvadrat kan vi skriveDet tilsvarende kan gjøres for og slik at vi fårSiden dette skal være lik null, og , kan vi altså skrive likningen for planet på formenDet betyr at kulen har radius og sentrum i .
Svar:
Mer om
Denne oppgaven er om Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius. Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Kule

Plan
Ligning
For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.
Visste du at
Likningen for en kuleflate kan alltid skrives på formender er sentrum og er kulens radius. Ved å multiplisere ut parentesene kan vi skrive likningen på formenHvis vi nå deriverer begge sider av likningen med hensyn på hver koordinat finner vi $$\begin{split} \mbox{med hensyn på $x$: }& 2x-2x_0=0 \implies x=x_0 \\ \mbox{med hensyn på $y$: }& 2y-2y_0=0 \implies y=y_0 \\ \mbox{med hensyn på $z$: }& 2z-2z_0=0 \implies z=z_0. \\ \end{split}$$ Dette betyr at vi kunne funnet kulens sentrum ved å derivere begge sider av likningen for kuleflaten med hensyn på hver variabel, der vi tenker på de andre variablene som konstante, og bruke dette til å løse for , og .
c)
Bestem en likning for tangentplanet til kulen i punktet .
Løsningsforslag c)
Jeg tenker
Siden vi både kjenner kulens sentrum og et punkt på kulens overflate kan vi uttrykke tangentplanet til kulen ved å konstruere normalvektoren .
Hvis er kulens sentrum og er et punkt på kuleflaten må vektorengå gjennom sentrum i kulen og derfor stå normalt på kuleflaten. Tangentplanet i punktet , som består av alle punkter inneholdt i en linje som tangerer kulen i punktet , må derfor ha vektoren som normalvektor. Det betyr at alle vektorer mellom to punkter i tangentplanet må stå vinkelrett på og derfor tilfredsstille. Siden ligger i tangentplanet må alle punkter som ligger i tangentplanet altså tilfredsstille likningenSiden
kan likningen for tangentplanet i altså skrives
Svar:
Mer om
Denne oppgaven er om Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius. En normalvektor for et plan står vinkelrett på alle linjer i planet. Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.Kule

Normalvektor
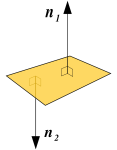
Tangent

Ligning
Plan
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
Oppgave 6 (4 poeng) Nettkode: E-4DKI
Følgende formler er gitt:
a)
Bruk formlene ovenfor til å uttrykke og ved og .
Løsningsforslag a)
Jeg tenker
Siden formelen for sinus til summen av to vinkler skal holde for alle par, og , av vinkler må den også holde når .
Ved å sette de to vinkelene like hverandre og gi dem navnet , det vil si , kan vi skriveogDersom det skulle være ønskelig kan man bruke identiteten til å skrive sistnevnte på formen
Svar:
Mer om
Denne oppgaven er om
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere forklaringer og eksempler på trigonometri, se artikkelen Trigonometriske formler.
Visste du at
Et viktig resultat innen matematikk er likningender . Dersom vi ikke bryr oss om hvor rart det er å jobbe med et tall som har egenskapen kan vi med likningen definere sinus og cosinus vedVed hjelp av disse definisjonene kan vi finne alle de formlene for cosinus og sinus som vi tidligere har blitt bedt om bare å pugge. For eksempel kan vi ved å sammenlikneogdele leddene som inneholder fra de som ikke inneholder . Da finner vi atsom er det vi har vist i denne oppgaven.
b)
Vis at
Løsningsforslag b)
Jeg tenker
Siden uttrykket for må holde for alle mulige verdier av og må det også holde når .
Ved å settekan vi skrive den oppgitte formelen for sinus til en sum av to vinkler somMed andre ord har vi atVed å benytte resultatet fra oppgave kan vi skriveVed å benytte identiteten til å uttrykke som følger det atsom er det vi ønsket å vise.
Mer om
Denne oppgaven er om Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. Cosinus er en trigonometrisk funksjon. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Sinus
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Ligning
For flere forklaringer og eksempler på trigonometri, se artikkelen Trigonometriske formler.
Oppgave 7 (6 poeng) Nettkode: E-4DKL
Punktene , og er gitt.
a)
Bestem ved regning vektorproduktet .
Løsningsforslag a)
Jeg tenker
For å beregne vektorproduktet må vi først finne et uttrykk for vektorene og .
Med punktene , og kan vi konstruere vektorene
Vektorproduktet blir da
Svar:
Mer om
Denne oppgaven er om
Vektor

En vektor er en størrelse med en retning.
I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.
Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .
For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt av to vektorer.
b)
Forklar at ikke ligger på linjen gjennom og .
Løsningsforslag b)
Jeg tenker
Punktet ligger på linjen gjennom og hvis, og bare hvis, det finnes et tall slik at .
Siden linjen gjennom og kan parametriseres ved
ligger punktet på linjen hvis, og bare hvis, det finnes en slik at
Ved å sette hver av koordinatene lik hverandre og løse for finner vi imidlertid at
Siden ikke alle verdiene for er like kan vi ikke konkludere med noe annet enn at punktet ikke ligger på linjen gjennom og .
Alternativ løsning
Fra oppgave har vi atEttersom vektorproduktet mellom to parallelle vektorer alltid er null kan ikke vektorene og være parallelle. Det betyr at de tre punktene , og ikke kan ligge på samme rette linje. Med andre ord ligger ikke punktet på linjen gjennom og .
Svar: ligger ikke på linjen gjennom og .
Mer om
Denne oppgaven er om En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger. To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler. Eksempel: , leses "linja g er parallell med linja f". En vektor er en størrelse med en retning. I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren. Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = .Linje
Parallell

Tegnet som forteller at to linjer er parallelle: Vektor

For flere forklaringer og eksempler på vektorer, se artikkelen Parameterframstilling av en rett linje.
c)
Bestem en likning for planet gjennom , og .
Løsningsforslag c)
Jeg tenker
Ved å finne et uttrykk for normalvektoren til planet og minst ett punkt i kan vi skrive likningen som bestemmer planet.
I oppgave fant vi at
som kan skrives
Siden denne vektoren står normalt på alle vektorer mellom punkter i planet bør vi velge normalvektoren til slik at den er parallell med . Siden lengden ikke har noe å si kan vi altså velge normalvektoren
Siden ligger i må alle punkter i altså tilfredsstille
Ettersom
kan vi skrive likningen for planet som
Svar:
Mer om
Denne oppgaven er om Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En normalvektor for et plan står vinkelrett på alle linjer i planet. I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B. To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler. Eksempel: , leses "linja g er parallell med linja f". En linje som står 90 grader på en annen linje.Plan
Normalvektor

Punkt

Parallell

Tegnet som forteller at to linjer er parallelle: Normal
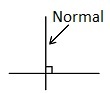
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
d)
Avgjør om punktet ligger i .
Løsningsforslag d)
Jeg tenker
Et punkt ligger i planet hvis, og bare hvis, koordinatene til punktet tilfredsstiller likningen for planet.
For å sjekke om punktet ligger i planet setter vi inn koordinatene i likningen for planet og ser om likningen er sann. Dette girAltså ligger punktet ikke i planet .
Svar: ligger ikke i .
Mer om
Denne oppgaven er om I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B. Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate. En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente. Eksempel: Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet. Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat. Se KoordinatsystemPunkt

Plan
Ligning
Koordinat
For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.
Oppgave 8 (3 poeng) Nettkode: E-4DKQ
Løs differensiallikningen
Løsningsforslag
Jeg tenker
Vi må finne en funksjon som tilfredsstiller differensiallikningen og har . Siden den ene siden bare avhenger av og den andre bare avhenger av kan det være lurt å begynne med å integrere begge sider av likningen.
Ved å integrere begge sider av differensiallikningenmed hensyn på og gjenkjenne substitusjonsmetoden med substitusjonen finner viSiden den deriverte av er finner vi videre atder er en konstant. Vi må legge til fordi uansett hvilken verdi konstanten har, er den deriverte av lik . Vi har altså funnet at må tilfredsstilleSiden den deriverte av er uansett verdien av konstanten finner vi videre atVed å samle de to konstantene til én konstant kan får viSiden må vi ha
Vi har altså funnet løsningensom kan skrives
Svar:
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Integrasjon
Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.
Se Integralregning
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.
Visste du at
Ved å gjenkjenne kjerneregelen for derivasjon i uttrykketkan vi skrive og og dermed forenkle likningen tilVed å integrere på begge sider av likningen med hensyn på finner vi da atHvis vi setter inn for og følger det da atsom er den genrelle løsningen av differensiallikningen.
Oppgave 9 (3 poeng) Nettkode: E-4DKS
Bruk induksjon til å bevise påstanden
Løsningsforslag
Jeg tenker
For å bevise påstanden for med induksjon må vi vise at og at hvis , så må nødvendigvis også .
Vi begynner med å sette inn for . Da sier påstanden atAltså er sann. Vi antar deretter at påstanden stemmer for . Det vil si atBetyr dette nødvendigvis at er sann? Påstanden sierog siden vi har antatt at stemmer kan vi skrive dette somVed å trekke fra på begge sider følger det atsom betyr at er sann så lenge er sann. Fra disse to resulatene følger det at er sann for alle ved induksjon.
Mer om
Denne oppgaven er om
Matematisk induksjon
En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:
- Bevis påstanden for n =1.
- Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).
Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).
Sum
Resultatet av en addisjon.
Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4DKU
En funksjon er gitt ved
a)
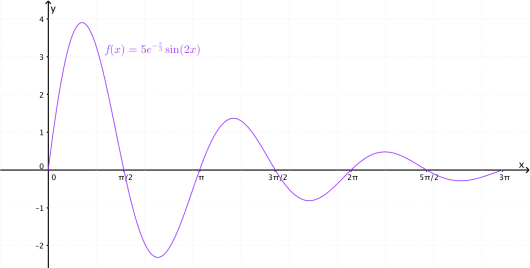
Bruk graftegner til å tegne grafen til for .
Løsningsforslag a)
Jeg tenker
Ved å benytte GeoGebra kan vi tegne grafen til på intervallet .
Ved å skrive kommandoenf(x):=Dersom[0<=x<= 3*pi, 5exp(-x/3)sin(2x)]
i geoGebras grafdel får vi følgende figur:
Mer om
Denne oppgaven er om
Intervall
Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).
Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Pi (π)
er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
For flere forklaringer og eksempler på grafer, se artikkelen Grafen til en funksjon.
b)
Bestem nullpunktene til i intervallet .
Løsningsforslag b)
Jeg tenker
Nullpunktene til en funksjon er nøyaktig de verdiene for som gjør at .
Nullpunktene er de verdiene for som tilfredsstiller likningenSiden aldri blir null må dette bety atVed å huske på enhetssirkelen, der er -verdiene til punktene på sirkelen, følger det at
og derfor
Nullpunktene i intervallet er altsåDette passer godt overens med grafen i oppgave .
Svar:
Mer om
Denne oppgaven er om Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Sirkel brukes i to betydninger: 1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets. Areal: Nullpunkt

Intervall
Sinus
Eksponentialfunksjon

Pi (π)
Graf
Sirkel

2) Flaten som sirkellinjen begrenser.
Omkrets:
For flere forklaringer og eksempler på likninger, se artikkelen Trigonometriske likninger.
c)
Bestem topp- og bunnpunktene på grafen til i intervallet .
Løsningsforslag c)
Jeg tenker
Topp- og bunnpunktene til en funksjon er punktene der den deriverte, , skifter fortegn.
Vi finner først et uttrykk for den deriverte av funksjonen vedSiden alle topp- og bunnpunkter må være slik at skifter fortegn i kan vi kreve , som betyr atEttersom aldri blir lik må da $$\begin{split} & 6\cos (2x)-\sin (2x) = 0 \\ \implies & 6\cos (2x)=\sin (2x) \\ \implies & \tan (2x) = 6. \end{split}$$ Dette skjer når
De forskjellige topp- og bunnpunktene på intervallet er dermed tilnærmet likVed enten å referere til figuren i oppgave eller å se at veksler mellom å være positiv og negativ, og at den begynner som positiv i , må annen hver av punktene vi fant ovenfor være toppunkt og bunnpunkt. Det betyr at vi har funnet punktene
Alternativ løsning
Ved å bruke de to kommandoene:f(x) = Dersom[0 <= x <= 3*pi, 5exp(-x/3)sin(2x)]
ogEkstremalpunkt[f, 0, 3*pi]
i geoGebras grafdel finner vi samme resultat, nemlig
Svar:
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju). Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt . Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt . Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. Cosinus er en trigonometrisk funksjon. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex.Graf
Intervall
Toppunkt

Bunnpunkt

Sinus
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Eksponentialfunksjon

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.
d)
Bestem arealet begrenset av grafen til og -aksen mellom og .
Løsningsforslag d)
Jeg tenker
Siden er positiv på intervallet er arealet begrenset av grafen til og -aksen mellom og er nøyaktig lik verdien av integralet .
Arealet, , begrenset av grafen til og -aksen mellom og er gitt som integraletDette integralet ser så vanskelig ut at vi bør gi det et navn. La derforslik at . Vi utfører nå delvis integrasjon ved å integrere og derivere . Det girSiden dette ikke hjalp forsøker å med nok en delvis integrasjon der vi fortsatt integrerer , men deriverer . Det gir
Vi har altså fått tilbake det integralet vi begynte med. Ved å bytte ut dette med navnet vi ga integralet, som var , og løse for følger det at
Arealet begrenset av grafen til og -aksen mellom og er altså
Alternativ løsning
Ved først å definere funksjonen ved å bruke kommandoenf(x) = Dersom[0 <= x <= 3*pi, 5exp(-x/3)sin(2x)]
i GeoGebras grafdel, og deretter utføre integralet med kommandoenIntegral[abs(f(x)), 0, pi/ 2]
finner vi at arealet begrenset av grafen til og -aksen mellom og er
Svar:
Mer om
Denne oppgaven er om Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen. Se Integralregning Cosinus er en trigonometrisk funksjon. Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.Integrasjon
Cosinus

Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.Sinus
Eksponentialfunksjon

Areal
Noen måleenheter for areal er m2, dm2 og cm2.Graf
For flere forklaringer og eksempler på integrasjon, se artikkelen Integraler som kan løses ved delvis integrasjon.
Oppgave 2 (3 poeng) Nettkode: E-4DKZ
Vis at er en løsning av differensiallikningen
og
Løsningsforslag
Jeg tenker
En funksjon er en løsning av en differensiallikning hvis den, sammen med sine deriverte , ,..., tilfredsstiller differensiallikningen.
La . For å vise at funksjonen er en løsning av differensiallikningen holder det å beregne de deriverte til og se om de tilfredsstiller likningen
Den førstederiverte av
, altså , erDet betyr at vi kan finne den andrederiverte, altså , vedHvis skal tilfredsstille differensiallikningen må altsåDet kan vi skrive somVed å multiplisere begge sider av likningen med kan vi skrive dette somAltså tilfredsstiller differensiallikningen. Da gjenstår det bare å undersøke om
Ved å sette inn for i finner vi atog ved å sette inn for i finner viAltså tilfredsstiller funksjonen differensiallikningen
Mer om
Denne oppgaven er om
Differensiallikning
En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.
Et eksempel er y'' - y = 0 eller
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Andrederiverte
Den andrederiverte til en funksjon er funksjonen derivert to ganger og skrives eller . Kalles også annenderiverte eller dobbeltderiverte.
For flere forklaringer og eksempler på differensiallikninger, se artikkelen Andre ordens differensiallikninger.
Oppgave 3 (6 poeng) Nettkode: E-4DLA
Vi skal i denne oppgaven studere nærmere som er gitt i oppgave 1 i Del 2.
a)
Vis at nullpunktene til i oppgave 1 danner en aritmetisk tallfølge Bestem .
Løsningsforslag a)
Jeg tenker
En aritmetisk tallfølge er en følge av tall som har den egenskapen at differansen mellom to etterfølgende tall, , alltid er den samme.
Nullpunktene til funksjonen er nøyaktig de verdiene for som tilfredsstiller likningenSiden aldri kan bli null betyr dette atAltså er de -verdiene som tilfredsstiller gitt ved
Siden bare er definert på intervallet er nullpunktene gitt ved
Hvis vi nå navngir nullpunktene vedfår vi en følge av tall. Denne følgen er en aritmetisk følge sidener en konstant uavhengig av . Det 20ende tallet i denne følgen er
Svar:
Mer om
Denne oppgaven er om
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Intervall
Et intervall er det samme som et tallområde. Tallene 4, 5, 6 og 7 ligger i intervallet 4–7 (fire til sju).
Dersom vi ikke har sagt noe annet, lar vi øvre og nedre grense høre med til intervallet.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere forklaringer og eksempler på rekker, se artikkelen Aritmetiske tallfølger.
b)
Vis at maksimalverdiene til i oppgave 1 danner en geometrisk tallfølge Bestem .
Løsningsforslag b)
Jeg tenker
En geometrisk tallfølge er en følge av tall som er slik at er en konstant uavhengig av .
I oppgave fant vi at ekstremalverdiene til var gitt ved
Vi fant også at det første punktet, og deretter annen hver, av disse punktene var et toppunkt. Med andre ord er toppunktene til funksjonen gitt ved -verdiene
Maksimalverdiene for er altså gitt ved tallfølgen
Siden
er en konstant som er uavhengig av er denne tallfølgen en geometrisk tallfølge. Verdien av det femte tallet i denne tallfølgen er
Svar:
Mer om
Denne oppgaven er om Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant. En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten. Brukes mest om funksjonen ex. Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .Sinus
Eksponentialfunksjon

Toppunkt

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske tallfølger.
c)
Begrunn at den uendelige rekken konvergerer. Bestem summen av rekken.
Løsningsforslag c)
Jeg tenker
At en uendelig rekke konvergerer betyr at den tar en veldefinert verdi som er mindre enn uendelig.
Rekken har første ledd og kvotient . Siden , er rekka konvergent med sum
Svar:
Mer om
Denne oppgaven er om
Sum
Resultatet av en addisjon.
Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.
Uendelige rekker
En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.
Eksempel :
( ∞ er tegnet for uendelighet )
Konvergens
Konvergens betyr i matematikk å nærme seg en grense.
Se Konvergent tallfølge
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
For flere forklaringer og eksempler på rekker, se artikkelen Uendelige rekker.
Oppgave 4 (3 poeng) Nettkode: E-4DLV
En kule har sentrum i og radius .
En linje går gjennom punktene og .
Bestem skjæringspunktene mellom linjen og kulen .
Løsningsforslag
Jeg tenker
Ved å parameterisere linjen og finne et uttrykk for likningen til kuleflaten kan vi kombinere disse for å finne skjæringspunktene mellom linjen og kulen .
Likningen for en kuleflate med radius og sentrum i erAltså må likningen for kuleflaten være gitt somVidere vet vi at siden den rette linjen går gjennom punktene og kan den parametriseres vedVed å sette inn koordinatene for linjen i likningen for kuleflaten kan vi nå bestemme skjæringspunktene mellom og . Det gir
Siden vi kan skrive venstresiden av likningen
følger det at skjæringspunktene er gitt ved
Skjæringspunktene er gitt ved
Svar: De to skjæringspunktene er altså gitt ved
Mer om
Denne oppgaven er om
Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.
Oppgave 5 (6 poeng) Nettkode: E-4DN3
Funksjonen er gitt ved
Grafen har toppunkt i . Se skissen nedenfor.
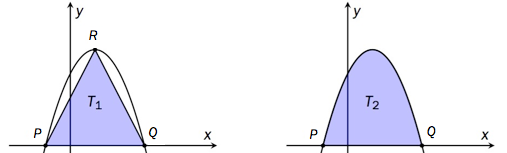
a)
Forklar at grafen til skjærer -aksen i punktene
og
der ligger til venstre for .
Løsningsforslag a)
Jeg tenker
Grafen til en funksjon skjærer -aksen i nøyaktig de -verdien som tilfredsstiller
Grafen til skjærer -aksen når . Det betyr atVed å huske annengradsformelen kan vi bruke at -verdiene som løser denne likningen er nøyaktig de to punktene gitt av
Disse er faktiske, reelle punkter ettersom og betyr at . Siden måsom betyr at må ha lavere -verdi enn og derfor ligge til venstre for .
Alternativ løsning
Dersom vi ikke husker annengradslikningen kan vi alltids løse likningen på egenhånd. Vi begynner med å dele på på begge sider og deretter trekke fra . Det girVi kan deretter fullføre kvadratet på venstresiden og dermed skrivesom kan omskrives tilVed å ta kvadratroten og deretter trekke fra på begge sider følger det at
Siden -verdien i disse punktene er lik følger det at grafen til skjærer -aksen i punktene
Siden måsom betyr at må ha lavere -verdi enn og derfor ligge til venstre for .
Dersom vi ikke husker annengradslikningen kan vi alltids løse likningen på egenhånd. Vi begynner med å dele på på begge sider og deretter trekke fra . Det girVi kan deretter fullføre kvadratet på venstresiden og dermed skrivesom kan omskrives tilVed å ta kvadratroten og deretter trekke fra på begge sider følger det at
Siden -verdien i disse punktene er lik følger det at grafen til skjærer -aksen i punktene
Siden måsom betyr at må ha lavere -verdi enn og derfor ligge til venstre for .
Mer om
Denne oppgaven er om
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
For flere forklaringer og eksempler på andregradslikninger, se artikkelen Å fullføre kvadratet.
b)
Bruk CAS til å vise at arealet til er gitt ved
Løsningsforslag b)
Jeg tenker
Siden grafen til har toppunkt i og -koordinaten til er høyden i kan vi bruke formelen for arealet av en trekant til å beregne arealet .
Vi begynner med å definere punktene og ved å bruke kommandoeneP := ( (-b+sqrt(b^2-4ac) )/(2a),0 ) Q := ( (-b-sqrt(b^2-4ac) )/(2a),0 )
Deretter definerer vi funksjonen vedf(x):=a x^2+b x+c
og løser likningen for å finne -koordinaten til Løs[Derivert[ f(x) ]=0]
Siden resultatet er definerer vi høyden til punktet som H:=f( -b/(2a) )
Siden bredden av er differansen følger det at arealet er gitt somH*( x(Q)-x(P) )/2
Svar: Resultatet er
Mer om
Denne oppgaven er om En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En trekant er en todimensjonal figur med tre hjørner og tre sidekanter. En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden). Eksempel: For funksjonen , vil alltid gi Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .Graf
Areal
Noen måleenheter for areal er m2, dm2 og cm2.Trekant

Funksjon
Toppunkt

For flere forklaringer og eksempler på trekanter, se artikkelen Geometri - areal og volum.
Visste du at
Det er ekstremt nyttig å kunne bruke dataprogrammer til å løse matematiske problemer. Denne oppgaven er imidlertid et eksempel på en situasjon der det er mye lettere å regne analytisk. En måte å finne arealet av trekanten er ved først å erkjenne at toppunktet har en -verdi som ligger midt mellom punktene og . Altså må ha -koordinat lik og dermed -koordinat gitt vedSiden dette er høyden i trekanten med grunnlinje følger det at arealet av trekanten er
som er det vi ønsket å vise.
c)
Bestem arealet mellom grafen til og -aksen.
Løsningsforslag c)
Jeg tenker
er arealet under grafen til mellom punktene og og kan derfor skrives som integralet.
Vi begynner ved å definere -koordinatene til og i CAS ved kommandoenex_Q :=(-b-sqrt(b^2-4ac))/(2a) x_P :=(-b+sqrt(b^2-4ac))/(2a)
Deretter finner vi ved å beregne integralet . Det gjør vi ved å bruke kommandoenIntegral[a x^2+b x + c, x_P , x_Q]
Resultatet blir da
Alternativ løsning
Siden er arealet under grafen til mellom punktene og kan det skrives
At den deriverte av er for alle betyr videre at
Siden
måogVidere følger det at
Vi kan altså uttrykke ved
Svar:
Mer om
Denne oppgaven er om Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er. En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene. I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B. En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.Areal
Noen måleenheter for areal er m2, dm2 og cm2.Graf
Punkt

Derivasjon
For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.
d)
Bestem forholdet .
Løsningsforslag d)
Jeg tenker
Ved å kombinere uttrykkene vi har for arealene og kan vi beregne forholdstallet .
Sidenogfølger det at
Svar:
Mer om
Denne oppgaven er om
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
For flere forklaringer og eksempler på brøk, se artikkelen Forkorte og utvide brøk.




