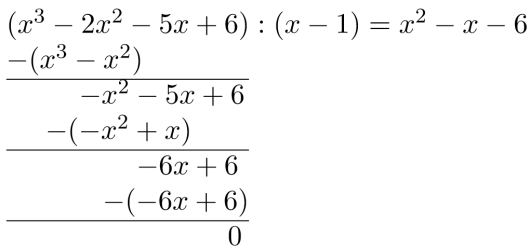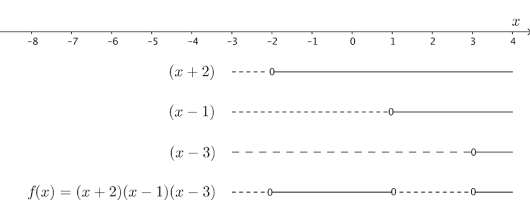Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3022 2015 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 9 oppgaver. Del 2 har 4 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og CAS skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.:
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4D51
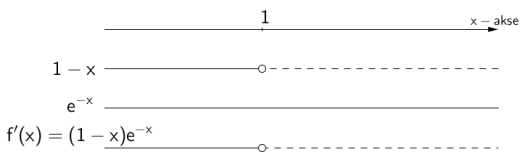
Deriver funksjonene
a)
b)
c)
Oppgave 2 (3 poeng) Nettkode: E-4D55
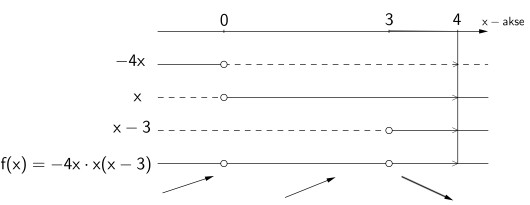
Funksjonen er gitt ved
Tegn fortegnslinjen til .
Oppgave 3 (5 poeng) Nettkode: E-4D57
Funksjonen er gitt ved
a)
Bestem slik at divisjonen går opp.
b)
I resten av oppgaven bruker vi denne k-verdien.
Faktoriser i lineære faktorer.
c)
Løs ulikheten .
Oppgave 4 (2 poeng) Nettkode: E-4D5B
Skriv så enkelt som mulig
Oppgave 5 (7 poeng) Nettkode: E-4D5D
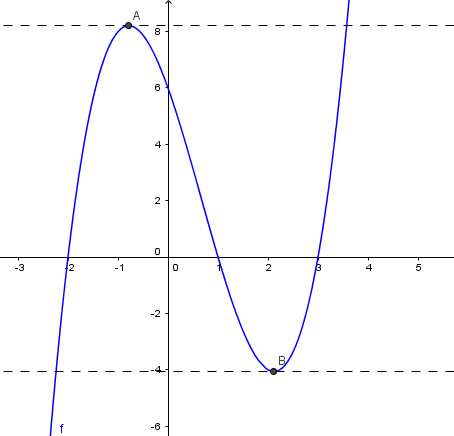
Funksjonen er gitt ved
a)
Bestem eventuelle nullpunkter til .
b)
Bestem eventuelle topp- og bunnpunkter på grafen til .
c)
Bestem eventuelle vendepunkter på grafen til .
d)
Lag en skisse av grafen til .
Oppgave 6 (3 poeng) Nettkode: E-4D5J
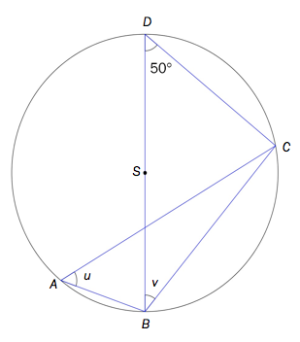
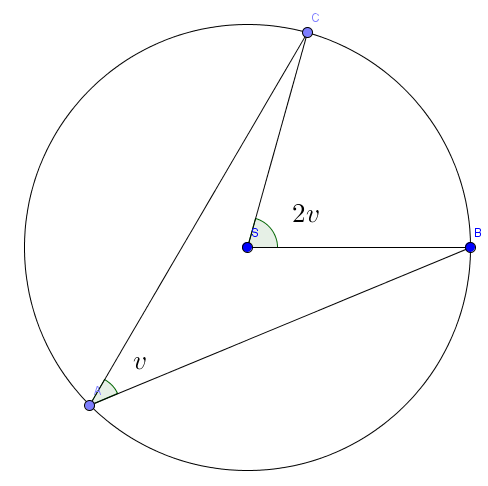
Skissen viser en sirkel med sentrum i . Punktene , , og ligger på sirkelen.
er en diameter.
Vi setter , og .
Bruk et geometrisk resonnement til å bestemme størrelsen på vinklene og .
Oppgave 7 (4 poeng) Nettkode: E-4D5L
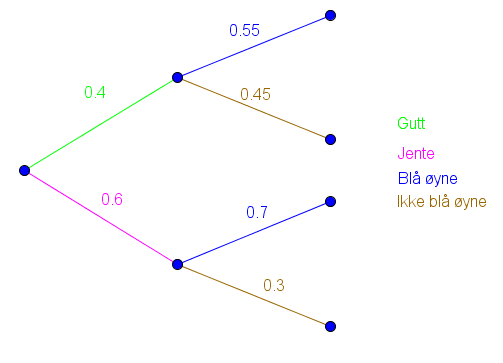
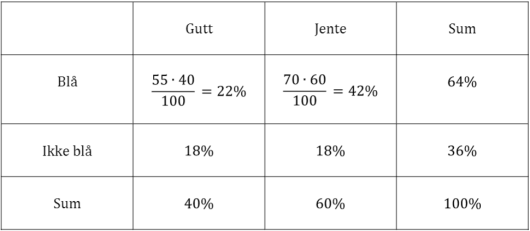
På en skole er 60 % av elevene jenter. 70 % av jentene og 55 % av guttene har blå øyne. Vi trekker ut en tilfeldig valgt elev ved skolen.
a)
Bestem sannsynligheten for at eleven har blå øyne.
b)
Eleven som er trukket ut, har ikke blå øyne. Bestem sannsynligheten for at eleven er en gutt.
Oppgave 8 (5 poeng) Nettkode: E-4D5O
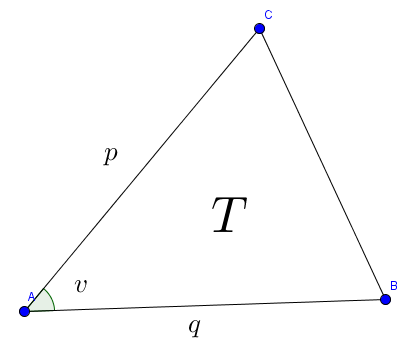
a)
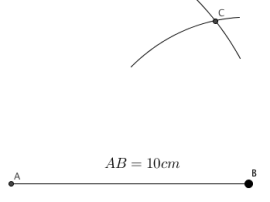
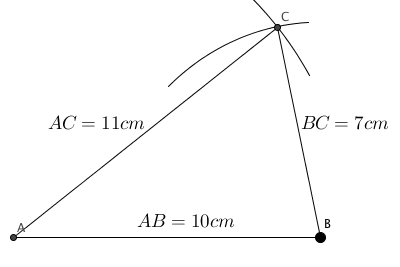
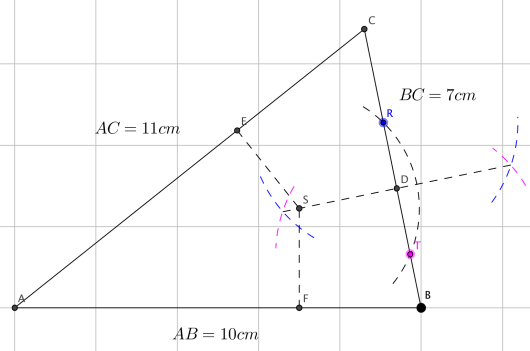
Konstruer en slik at cm, cm og cm.
b)
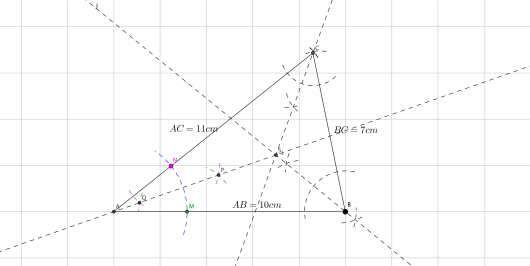
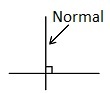
En skjæringssetning sier at halveringslinjene til de tre vinklene i trekanten skjærer hverandre i ett punkt.
Demonstrer denne setningen ved å konstruere halveringslinjene til vinklene i .
c)
Halveringslinjene skjærer hverandre i punktet .
Konstruer normalene fra ned på hver av sidekantene i . Fotpunktene til normalene kaller vi , og .
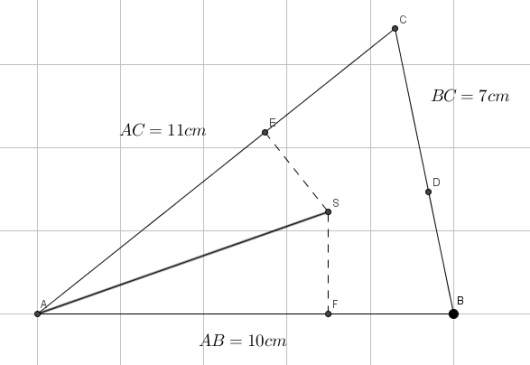
d)
Forklar at . Konstruer den innskrevne sirkelen i .
Oppgave 9 (2 poeng) Nettkode: E-4D5T
Løs likningen
DEL 2 Med hjelpemidler
Oppgave 1 (5 poeng) Nettkode: E-4D5V
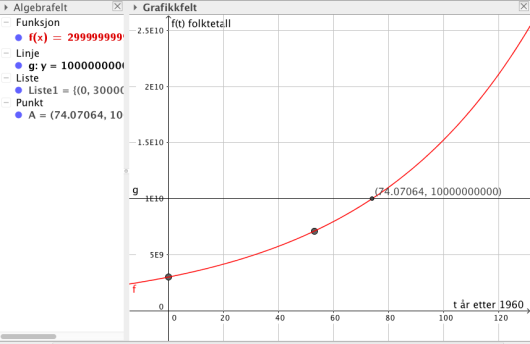
I 1960 var folketallet på jorden 3,0 milliarder. I 2013 var folketallet 7,1 milliarder. En god modell for utviklingen av folketallet er funksjonen gitt ved
der og er konstanter og tiden er antall år etter 1960.
a)
Bestem konstantene og .
b)
Når vil folketallet passere 10 milliarder ifølge denne modellen?
c)
Forklar at folketallet stiger med en fast prosent hvert år ifølge modellen.
Bestem denne faste, årlige prosenten.
Oppgave 2 (6 poeng) Nettkode: E-4D5Z
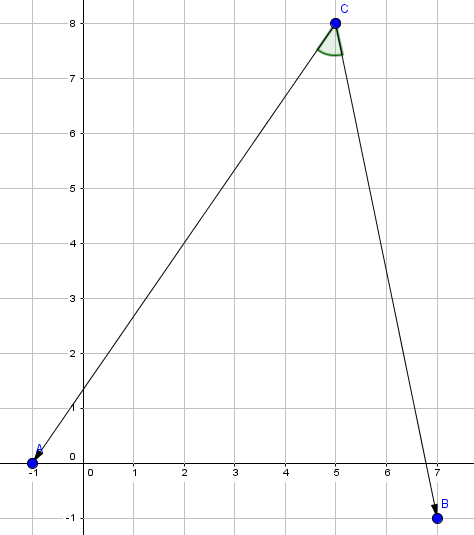
I et koordinatsystem er punktene , og gitt.
a)
Bestem , og .
b)
Bestem arealet til .
c)
Bruk vektorregning til å bestemme koordinatene til et punkt på -aksen slik at
Oppgave 3 (5 poeng) Nettkode: E-4D64
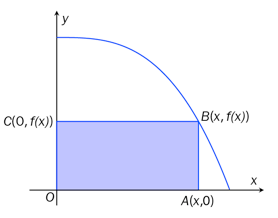
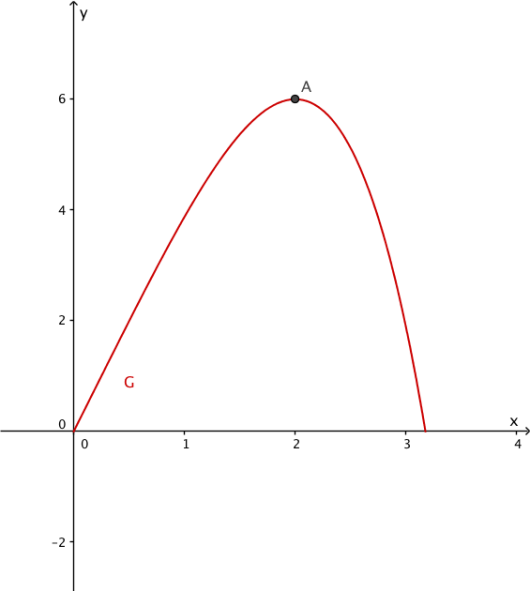
På figuren nedenfor ser du grafen til funksjonen gitt ved
Rektangelet er laget slik at ligger på grafen til .
a)
Vis at arealet til rektangelet kan skrives som
b)
Bestem slik at rektangelet får areal lik 5,0.
c)
Bestem det største arealet rektangelet kan ha.
Oppgave 4 (8 poeng) Nettkode: E-4D68
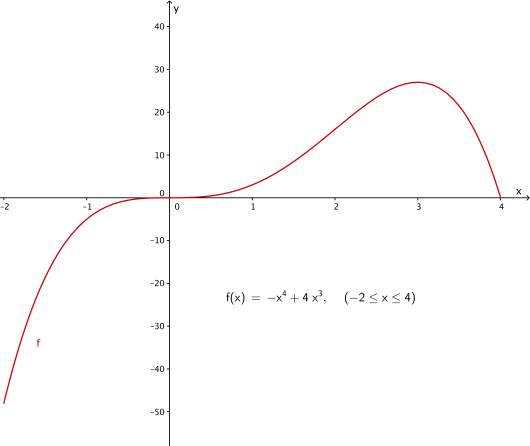
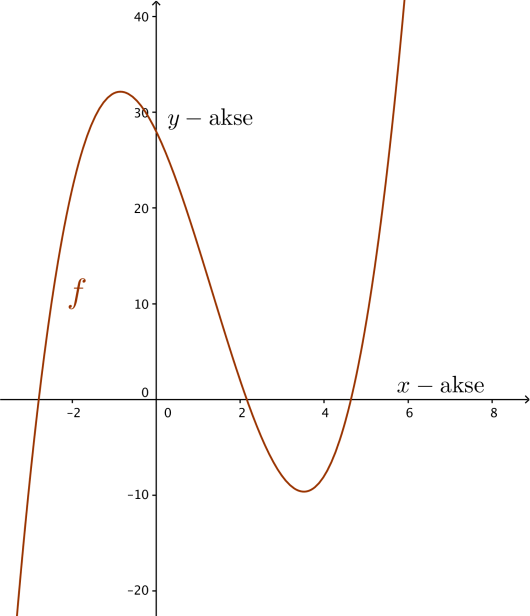
Funksjonen er gitt ved
a)
Bruk graftegner til å tegne grafen til .
b)
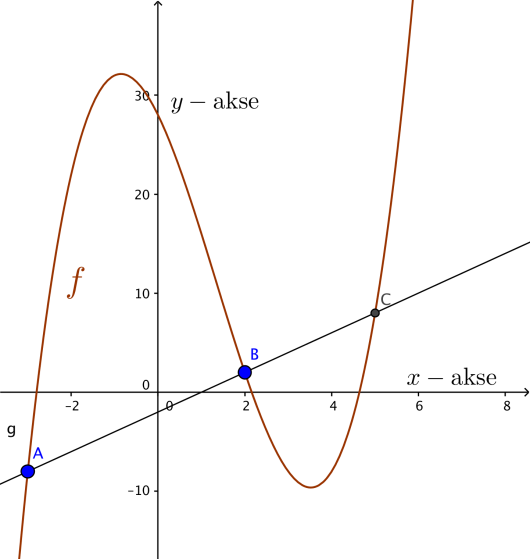
En linje skjærer grafen til i punktene og .
Bestem det tredje skjæringspunktet mellom grafen til og linjen. Hva blir summen av
-koordinatene til de tre skjæringspunktene?
c)
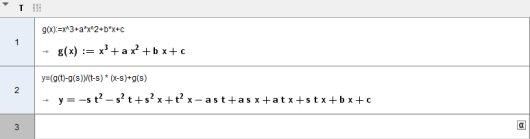
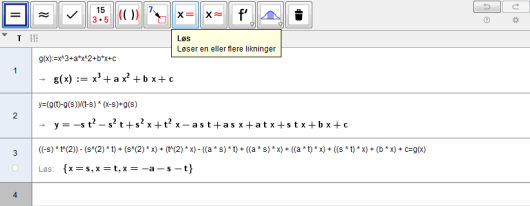
Funksjonen er gitt ved
En linje går gjennom punktene og .
Bruk CAS til å bestemme likningen for linjen , uttrykt ved , , , og .
d)
Bruk CAS til å bestemme -koordinaten til det tredje skjæringspunktet mellom grafen til og linjen . Bestem summen av -koordinatene til de tre skjæringspunktene.