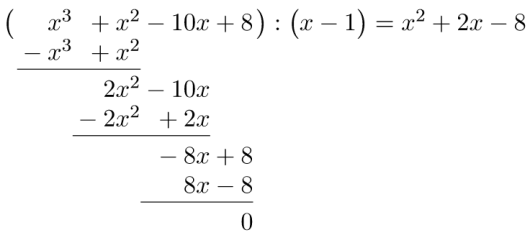Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3022 2014 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.:
- Alle grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4CYB
Deriver funksjonene
a)
b)
Oppgave 2 (4 poeng) Nettkode: E-4CYE
Polynomfunksjonen er gitt ved
a)
Faktoriser i førstegradsfaktorer.
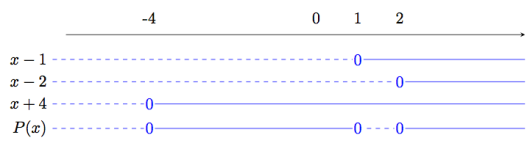
b)
Løs ulikheten .
Oppgave 3 (4 poeng) Nettkode: E-4CYH
Sammenhengen mellom lydstyrken db (desibel) og lydintensiteten W/m2 er gitt ved
er en konstant.
a)
Vis at formelen kan skrives som
b)
På en arbeidsplass blir lydintensiteten målt til W/m2.
Hvor mange desibel er lydstyrken på arbeidsplassen?
c)
På en klassefest blir lydstyrken målt til 100 dB.
Hvilken lydintensitet svarer det til?
Oppgave 4 (4 poeng) Nettkode: E-4CYL
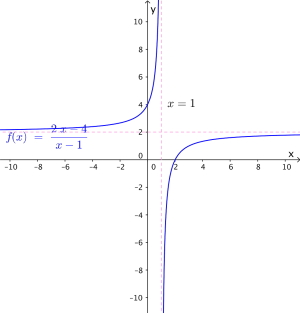
Funksjonen er gitt ved
\
a)
Lag en skisse av grafen til .
b)
Bestem .
c)
Bestem likningen til tangenten i punktet på grafen.
Oppgave 5 (2 poeng) Nettkode: E-4CYP
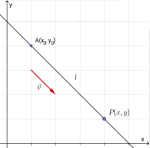
a)
Forklar at er en retningsvektor til linjen
b)
To linjer er gitt ved likningene og
Bruk skalarprodukt til å vise at dersom linjene står vinkelrett på hverandre, er .
Oppgave 6 (2 poeng) Nettkode: E-4CYS
Løs likningen
Oppgave 7 (4 poeng) Nettkode: E-4CYV
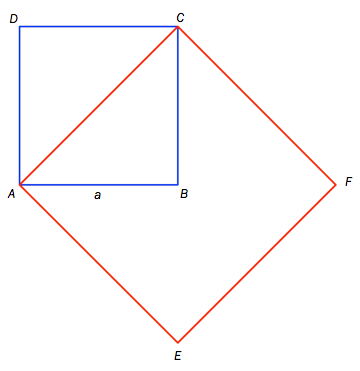
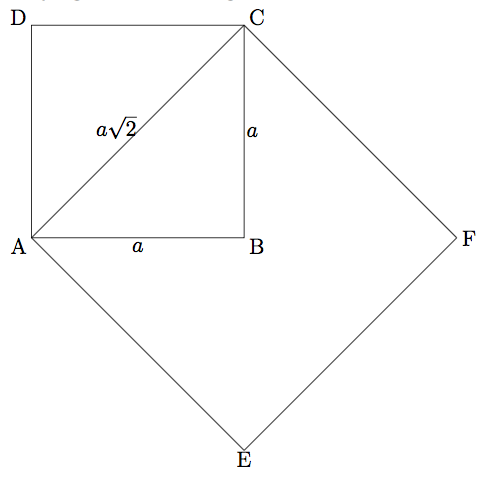
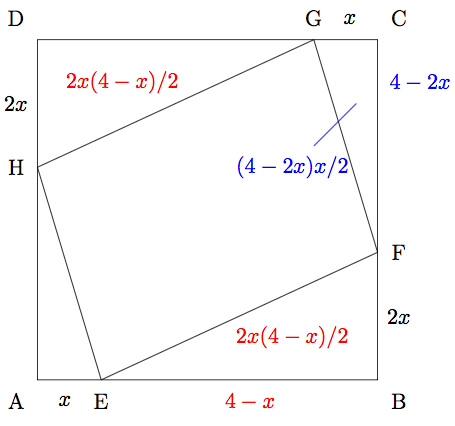
På figuren nedenfor har vi tegnet kvadratene og .
Vi setter siden i kvadratet lik .
a)
Vis at kvadratet AEFC har dobbelt så stort areal som kvadratet ABCD.
b)
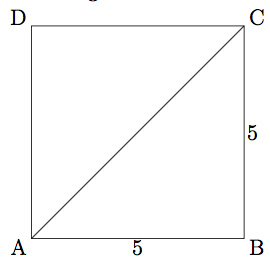
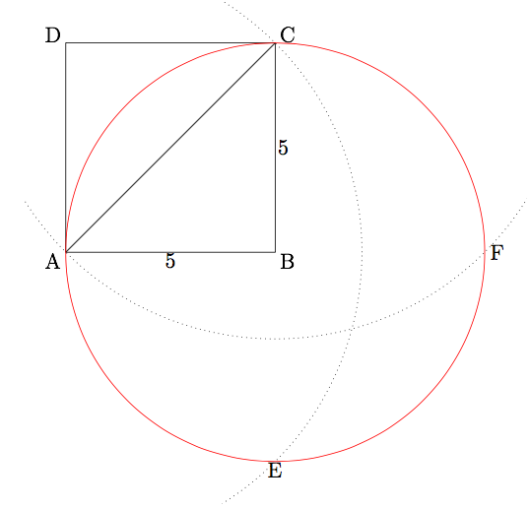
Konstruer et kvadrat med areal eksakt lik 50 cm2 .
Oppgave 8 (2 poeng) Nettkode: E-4CYY
Funksjonen er gitt ved
Bruk definisjonen av den deriverte til å vise at
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-4CZ0
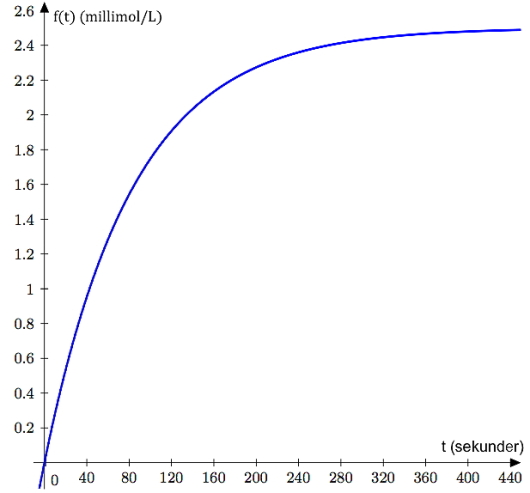
Ved en bestemt kjemisk reaksjon vil konsentrasjonen av et stoff være gitt ved
der er antall millimol per liter av stoffet, t sekunder etter at reaksjonen startet.
a)
Hva er konsentrasjonen etter 15 s?
Hvor lang tid tar det før konsentrasjonen er 2,00 millimol/L?
b)
Tegn grafen til .
Hva vil konsentrasjonen nærme seg dersom den kjemiske reaksjonen går veldig lenge?
c)
Reaksjonshastigheten på et tidspunkt er .
Hva er reaksjonshastigheten når konsentrasjonen er 2,00 millimol/L?
Oppgave 2 (5 poeng) Nettkode: E-4CZ4
a)
Skriv opp alle primtallene fra og med 2 til og med 25.
b)
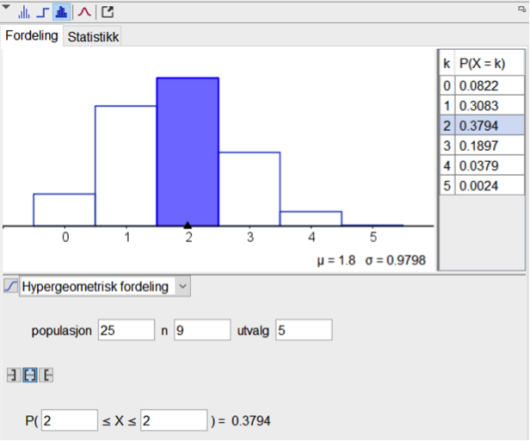
25 like kuler som er merket med tallene fra og med 1 til og med 25, ligger i en bolle. Vi trekker tilfeldig 5 kuler fra bollen uten tilbakelegging og leser av tallene.
Bestem sannsynligheten for at vi trekker ut akkurat 2 primtall.
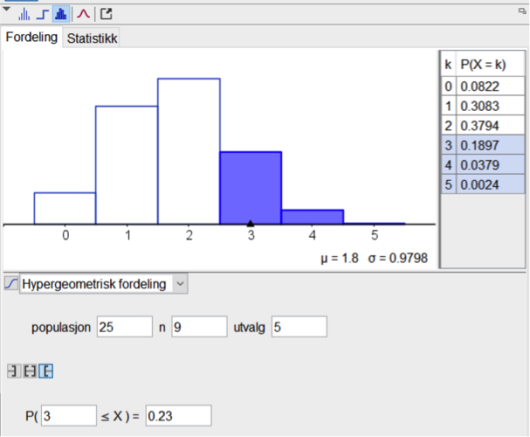
c)
Bestem sannsynligheten for at vi trekker ut minst 3 primtall.
Oppgave 3 (4 poeng) Nettkode: E-4CZ8
Vi har punktene , og .
a)
Bruk vektorregning til å bestemme slik at punktene , og ligger på en rett linje.
b)
Bruk vektorregning til å bestemme slik at .
Oppgave 4 (8 poeng) Nettkode: E-4CZC
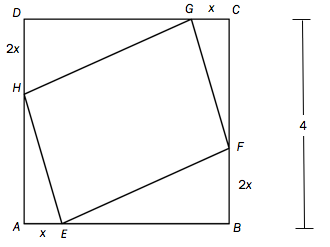
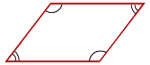
I et kvadrat med side 4 er det innskrevet et parallellogram . Vi setter og . Se skissen nedenfor.
a)
Vis at arealet av parallellogrammet er
b)
Bestem slik at arealet av parallellogrammet blir halvparten av arealet av kvadratet .
c)
Bestem slik at arealet av parallellogrammet blir minst mulig.
Bestem det minste arealet.
d)
Vi legger figuren inn i et koordinatsystem slik at ligger i origo og på positiv -akse.
Bestem vektorene og uttrykt ved og bruk dette til å bestemme slik at parallellogrammet blir et rektangel.
Oppgave 5 (6 poeng) Nettkode: E-4CZI
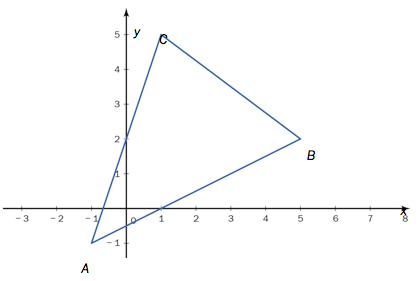
har hjørnene , og . Se figuren nedenfor.
Likningen for linjen gjennom og er , og likningen for linjen gjennom og er .
a)
Bestem likningen for linjen gjennom og .
b)
I oppgave 5 i Del 1 har du vist at dersom to linjer står vinkelrett på hverandre, er produktet av stigningstallene lik -1 .
Bruk denne egenskapen til å vise at linjen som går gjennom og som står vinkelrett på sidekanten har likningen .
c)
På samme måte kan det vises at linjen som går gjennom og som står vinkelrett på sidekanten har likningen , og linjen som går gjennom og som står vinkelrett på har likningen .
Vis ved regning at de tre høydene i skjærer hverandre i ett og samme punkt.
Bestem koordinatene til dette skjæringspunktet.
Oppgave 6 (3 poeng) Nettkode: E-4CZN
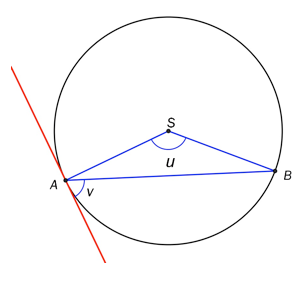
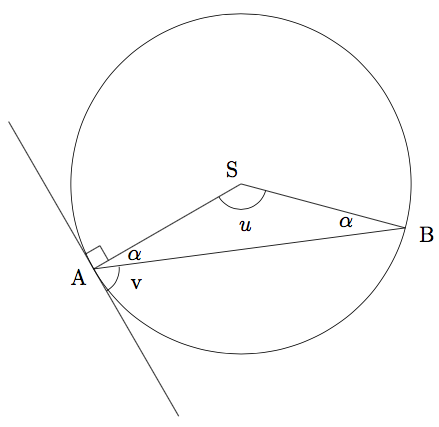
I en sirkel med sentrum S er det innskrevet en der . Sirkelen har en tangent i punktet . Vinkelen mellom tangenten og siden er .
a)
Vis at .
b)
Vis at .
Oppgave 7 (4 poeng) Nettkode: E-4CZQ
Funksjonen er gitt ved
der og er funksjoner av . Vi antar i denne oppgaven at og .
Logaritmeregelen for en brøk gir
a)
Bruk logaritmeregelen og kjerneregelen til å bestemme uttrykt ved , , og .
b)
Bruk uttrykket fra oppgave a) til å utlede derivasjonsregelen for en brøk.