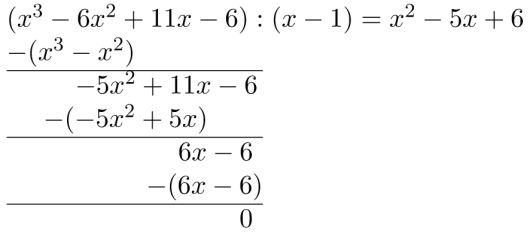Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

REA3022 2013 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Hippokrates (Utdanningsdirektoratet)
- Alle grafer og figurer (Utdanningsdirektoratet)
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4CWU
Formlene for arealet av en sirkel og volumet av en kule med radius er gitt ved
og
Bestem og .
Oppgave 2 (3 poeng) Nettkode: E-4CWW
Deriver funksjonene
a)
b)
Oppgave 3 (5 poeng) Nettkode: E-4CWZ
Polynomfunksjonen er gitt ved
a)
Vis at
b)
Bruk blant annet polynomdivisjon til å faktorisere i førstegradsfaktorer.
c)
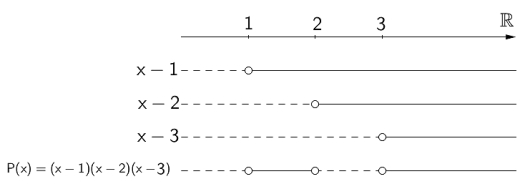
Løs ulikheten
Oppgave 4 (2 poeng) Nettkode: E-4CX3
Skriv så enkelt som mulig
Oppgave 5 (2 poeng) Nettkode: E-4CX6
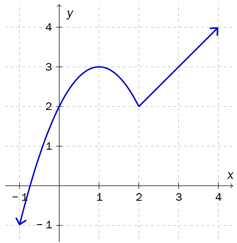
Figuren nedenfor viser grafen til en funksjon der
Avgjør for hvilke -verdier er kontinuerlig, og for hvilke -verdier er deriverbar.
Oppgave 6 (3 poeng) Nettkode: E-4CX8
En funksjon er gitt ved
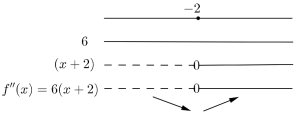
Vis at grafen til har en vendetangent i punktet med likning
Oppgave 7 (3 poeng) Nettkode: E-4CXA
Vektorene , og er gitt.
a)
Undersøk om
b)
Bestem ved regning to tall og slik at
Oppgave 8 (4 poeng) Nettkode: E-4CXE
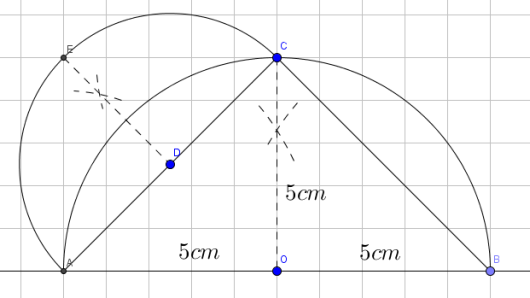
På figuren nedenfor er en halvsirkel med sentrum i , og er en halvsirkel med sentrum i .
a)
Konstruer figuren nedenfor når du setter cm . Ta med konstruksjonsforklaring.
b)
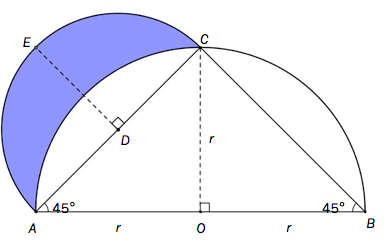
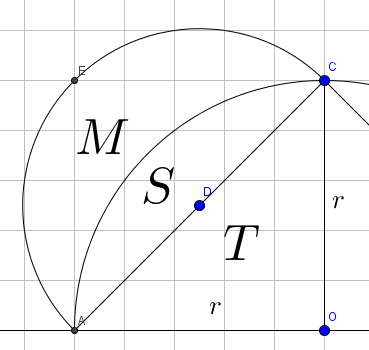
På figuren nedenfor har Hippokrates-månen blå farge.
Vis ved regning at arealet av Hippokrates-månen er lik arealet av når radien i halvsirkelen er .
DEL 2 Med hjelpemidler
Oppgave 1 (7 poeng) Nettkode: E-4CXK
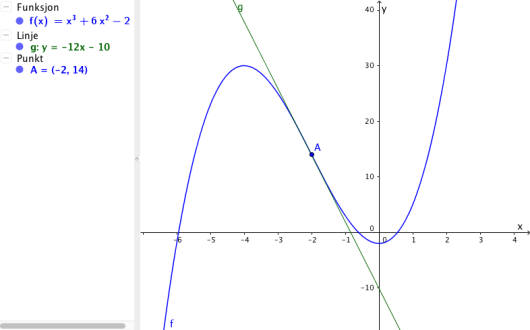
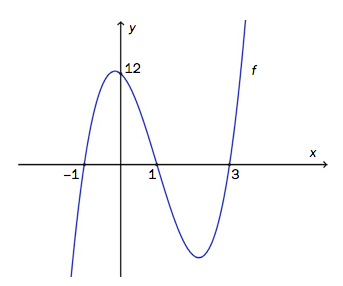
Figuren nedenfor viser grafen til en tredjegradsfunksjon .
a)
Forklar at er delelig med , og .
Begrunn at vi da kan skrive
, der er en konstant.
Bestem når punktet ligger på grafen til .
b)
Bestem likningen til tangenten i punktet .
c)
Denne tangenten skjærer grafen til i et annet punkt.
Bestem ved regning koordinatene til dette punktet.
Oppgave 2 (6 poeng) Nettkode: E-4CXP
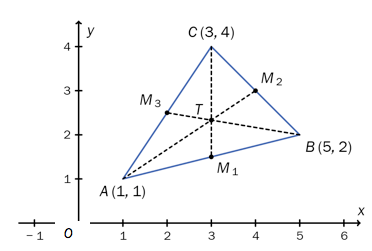
Se skissen nedenfor.
a)
Midtpunktene på sidekantene i er , og .
Vis ved regning at har koordinatene . Bestem koordinatene til og ved regning.
b)
Bestem en parameterframstilling til linjen gjennom og og en parameterframstilling til linjen gjennom og .
c)
Tyngdepunktet i trekanten er skjæringspunktet mellom medianene.
Bestem koordinatene til .
Oppgave 3 (7 poeng) Nettkode: E-4CXT
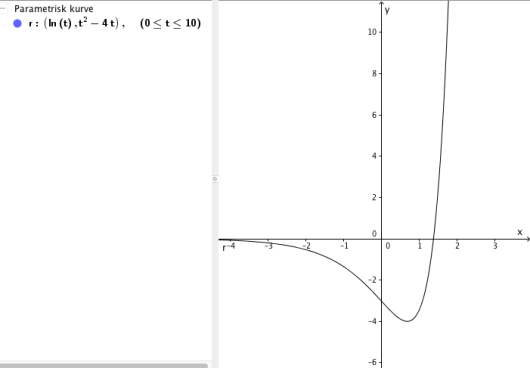
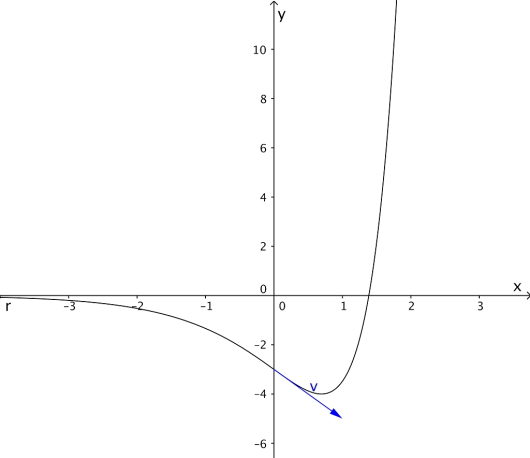
En partikkel har posisjonsvektoren
a)
Tegn grafen til og bestem skjæringspunktene med koordinataksene ved regning
b)
Bestem fartsvektoren og bruk denne til å bestemme eventuelle topp- og bunnpunkter på grafen til . Tegn inn på grafen.
c)
Vis at akselerasjonsvektoren er . Bestem når .
Kommenter svaret.
Oppgave 4 (8 poeng) Nettkode: E-4CXY
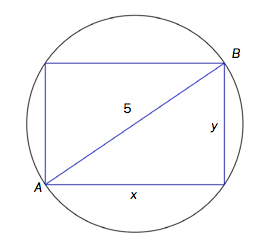
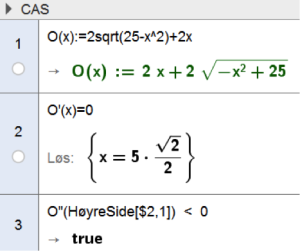
Et rektangel med sider og er innskrevet i en sirkel med diameter .
a)
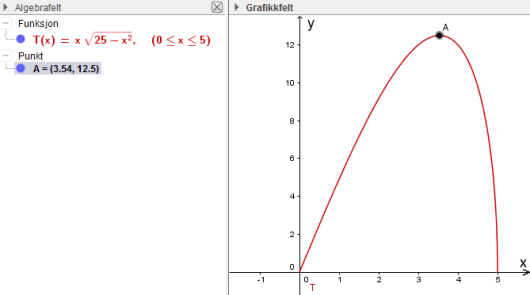
Vis at arealet av rektangelet er gitt ved
Forklar hvilke verdier kan ha.
b)
Bestem og når arealet er størst mulig.
Kommenter svaret.
c)
Vis at omkretsen til rektangelet er gitt ved
Bruk og bestem når omkretsen er størst mulig.
Kommenter svaret.
Oppgave 5 (6 poeng) Nettkode: E-4CY2
Vi har røde og svarte kuler i en eske. Vi skal trekke tilfeldig to kuler uten tilbakelegging. Vi definerer følgende hendelser:
A: Vi trekker to kuler med ulik farge.
B: Vi trekker to kuler med samme farge.
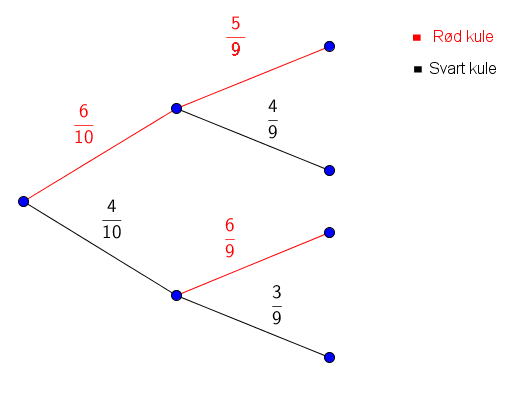
Anta at vi har 6 røde og 4 svarte kuler i esken.
a)
Bestem
b)
Bestem
c)
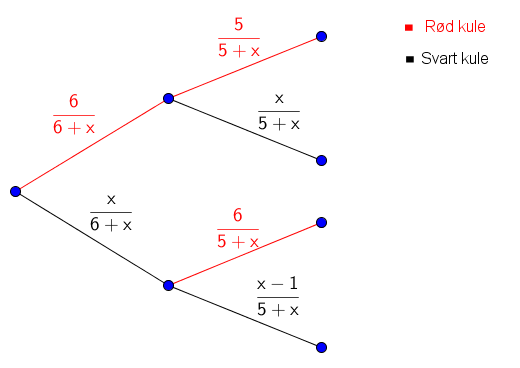
Anta at vi har røde og et ukjent antall svarte kuler i esken, og at hendelsene og skal ha lik sannsynlighet.
Hvor mange svarte kuler kan det være i esken?
Oppgave 6 (2 poeng) Nettkode: E-4CY6
Løs likningen