
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1015 2016 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Solkurve: http://suncurves.com/(15.10.2015)
- Lufttrykk: http://skolediskusjon.no/Forums/Thread.aspx?id=1160 (27.06.2015) http://www.yr.no/artikkel/mindre-trykk-og-varme-i-hoyden-1.7297472 (27.06.2015) http://www.yr.no/artikkel/hvordan-beregnes-lufftrykket_-1.7150434 (17.10.2015) http://naturfag.info/5jorden/b_atmosf.htm (17.10.2015)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (3 poeng) Nettkode: E-4CSZ
| Dato | Temperatur |
| 01.03. | |
| 02.03. | |
| 03.03. | |
| 04.03. | |
| 05.03. | |
| 06.03 |
Guro målte temperaturen utenfor hytta de seks første dagene i mars. Se tabellen ovenfor.
Bestem variasjonsbredden, gjennomsnittet og medianen for temperaturmålingene.
Løsningsforslag
Jeg tenker
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Vi starter med
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
Videre finner vi gjennomsnittet, som vi regner ut ved å legge sammen alle målingene og dividere med antall målinger. Guro målte temperaturen seks ganger, så gjennomsnittet er
Til slutt finner vi medianen. Det gjør vi ved å sette opp målingene i stigende (eller synkende) rekkefølge, og ta gjennomsnittet av de to midterste verdiene. Vi setter opp i stigende rekkefølge:De to midterste målingene er og , så medianen er .
Svar: Variasjonsbredden er , gjennomsnittet er og medianen er .
Mer om
Denne oppgaven er om
Variasjonsbredde
Variasjonsbredden i et datamateriale er differansen mellom den største verdien og den minste verdien.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
For flere forklaringer og eksempler på variasjonsbredde, gjennomsnitt og median, se artikkelene Variasjonsbredde, Gjennomsnitt og Median.
For å øve mer, se oppgavesettet om hovedtendenser i Treningsleiren.
Oppgave 2 (2 poeng) Nettkode: E-4CT2
Det er ca. 7,5 milliarder mennesker på jorda. Anta at hvert menneske trenger 2 L drikkevann hver dag.
Omtrent hvor mange liter drikkevann vil da alle menneskene på jorda til sammen trenge hver måned? Skriv svaret på standardform.
Løsningsforslag
Jeg tenker
Én milliard er det samme som . Husk hva et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Et
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi antar at det er dager i en måned. Det er milliarder, eller , mennesker på jorda. Hvis hvert av disse menneskene trenger vann per dag, blir detliter vann per dag, eller liter per måned. Dette tallet skal vi skrive på standardform. Det første vi gjør er å gjøre om til , og flytter alt som har med å gjøre på høyre side i stykket.Deretter regner vi ut hver parentes for seg. Først ser vi at . Videre ser at , så , eller . Dermed kan tallet over skrives som Igjen bruker vi potensreglene for potenser med samme grunntall, og vi får
Svar: liter vann per måned, gitt at én måned er 30 dager.
Mer om
Denne oppgaven er om
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
For flere forklaringer og eksempler på standardform, se artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.
Oppgave 3 (2 poeng) Nettkode: E-4CT4
I butikk A koster en vare 150 kroner. I butikk B koster den samme varen 120 kroner.
a)
Hvor mange prosent høyere er prisen i butikk A sammenliknet med prisen i butikk B?
Løsningsforslag a)
Jeg tenker
Vi skal finne ut hvor mange
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
I butikk koster varen av det den koster i butikk . Vi kan regne om brøken ved å faktorisere teller og nevner, og deretter forkorte.Det er det samme som . Derfor koster varen mer i butikk enn i butikk .
Svar: .
Mer om
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere forklaringer og eksempler på prosent, se artikkelen Prosent av hva da?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
b)
Hvor mange prosent lavere er prisen i butikk B sammenliknet med prisen i butikk A?
Løsningsforslag b)
Jeg tenker
Her skal vi finne ut hvor mange
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
I butikk koster varen av det den kostet i butikk . Vi regner ut brøken på samme måte som i forrige oppgave, og får Det er det samme som , så prisen til varen i butikk er av prisen i butikk . Dermed er prisen i butikk lavere enn i butikk .
Svar: lavere.
Mer om
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere forklaringer og eksempler på prosent, se artikkelen Hva er prosent?.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
Oppgave 4 (1 poeng) Nettkode: E-4CT7
Merverdiavgiften på klær er 25 %. En jakke koster 750 kroner med merverdiavgift.
Hvor mange kroner betaler vi i merverdiavgift dersom vi kjøper denne jakken?
Løsningsforslag
Jeg tenker
Merverdiavgift
Merverdiavgift er en avgift vi betaler når vi kjøper varer eller tjenester og er inkludert i prisen til varen eller tjenesten.
25 % for de fleste varer eller tjenester
15 % for mat og drikke
12 % for persontransport, kinobilletter og utleie av rom
For oppdaterte satser se Skatteetatens hjemmeside.
Vi viser to metoder å løse oppgaven på. Vi viser metoden der vi bruker
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
La oss si at jakken i utgangspunktet kostet kroner.
Merverdiavgift
Merverdiavgift er en avgift vi betaler når vi kjøper varer eller tjenester og er inkludert i prisen til varen eller tjenesten.
25 % for de fleste varer eller tjenester
15 % for mat og drikke
12 % for persontransport, kinobilletter og utleie av rom
For oppdaterte satser se Skatteetatens hjemmeside.
Alternativ løsning
Som nevnt kunne vi løst oppgaven på en annen måte. Vi sier at jakkens pris uten moms er . Vi skal legge til moms, og da må de kronene være av jakkens pris. Da må ett prosent være Den opprinnelige prisen til jakken var dermed
Svar: 150 kroner.
Mer om
Denne oppgaven er om
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
For flere forklaringer og eksempler på lineære likninger, se artikkelen Lineære likninger.
For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleiren.
Oppgave 5 (5 poeng) Nettkode: E-4CTD
| Alder | Frekvens |
| 40 | |
| 20 | |
| 60 | |
| 20 | |
| 20 | |
| 40 | |
| Sum | 200 |
Tabellen ovenfor viser aldersfordelingen for de 200 personene som bor i blokk Z på Tirilltoppen.
a)
Lag et histogram som viser aldersfordelingen for personene som bor i blokk Z.
Løsningsforslag a)
Jeg tenker
Vi må huske på at de forskjellige aldersintervallene har forskjellige lengder, og at det påvirker hvordan vi skal tegne stolpene i
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Husk at det er
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Det aller første vi gjør, er å tegne opp et passende
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.

Nå skal vi lage søylene våre. I aldersgruppen er det personer. Det betyr at vi skal lage en søyle som har grunnlinje (fordi det er så stort aldersintervallet er), og den skal ha areal (fordi det er personer i denne aldersgruppen). Da må høyden til søylen være . Tilsvarende må høyden på søylene til aldersgruppene og være henholdsvis og . I aldersgruppen er det personer. Denne søylen skal ha grunnlinje og areal , og da må høyden være . På samme måte regner vi ut at søylen tilhørende intervallet skal ha høyde , og at søylen tilhørende intervallet skal ha høyde . Resultatet er vist under.
Svar: 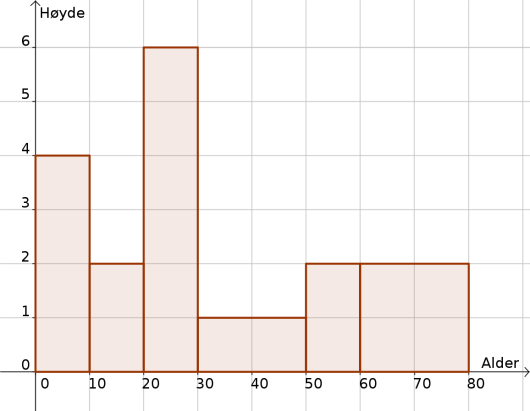
Mer om
Denne oppgaven er om
Histogram
Et histogram er et søylediagram der hver søyle viser frekvensen innenfor et tallintervall. Hele måleområdet er ofte delt inn i like store intervaller.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Verditabell
En tabell med verdier av en variabel, for eksempel , og tilhørende funksjonsverdier, for eksempel , kalles for en verditabell.
Verditabellen gir oss oversikt over verdier som hører sammen. Den hjelper oss enten med å finne punkter som ligger på grafen til en funksjon eller funksjonsuttrykket til en graf.
For flere forklaringer og eksempler på histogrammer, se artikkelen Histogram.
b)
Bestem gjennomsnittsalderen for personene som bor i blokka.
Løsningsforslag b)
Jeg tenker
Vi arbeider med gruppert informasjon. Da antar vi at dataene vi har er jevnt fordelt innenfor gruppene.
At dataene er jevnt fordelt innenfor gruppene, betyr for eksempel at gjennomsnittalderen av alle som er i intervallet er .
Det er personer som er mellom og år. Vi antar at gjennomsnittsalderen av disse er år. Når vi skal regne ut
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Svar: Cirka år
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere forklaringer og eksempler på gjennomsnitt, se artikkelen Gjennomsnitt.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.
c)
Aurora bor i blokk Z. Hun er 32 år. Hun vet at de yngste i blokka er nyfødte, og at den eldste er 79 år. Hun påstår derfor at hennes alder er lavere enn medianalderen.
Vurder om Auroras påstand er riktig.
Løsningsforslag c)
Jeg tenker:
Medianalderen regner man ut ved å sette opp aldrene til alle personene i stigende (eller synkende rekkefølge), og deretter velge det midsterste tallet, eventuelt
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Aurora tenker sannsynligvis det følgende: Den yngste som bor i blokken er år, mens den eldste er år. Hvis vi setter disse to tallene opp i stigende rekkefølge og tar
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Auroras påstand er feil, fordi vi glemmer bort alle de andre som bor i blokken, for eksempel Aurora selv. Det er personer som bor i blokk , og medianalderen er derfor gjennomsnittet av person nr. og person nr. , hvis vi setter dem opp med stigende alder. Vi ser fra tabellen at både person nr. og person nr. er mellom og år, så medianalderen er også det. Siden Aurora er over år, er hun over medianalderen.
Svar: Auroras påstand er feil fordi den ikke tar hensyn til alle de andre personene som bor i blokken.
Mer om:
Denne oppgaven er om
Median
Medianen er den verdien som vi finner i midten av et rangert datamateriale.
Eksempel: I et datamateriale har vi verdiene 3, 6, 1, 4 og 5. Vi rangerer verdiene til 1, 3, 4, 5, 6. Den midterste verdien er 4. Medianen er 4.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere forklaringer og eksempler på median, se artikkelen Median.
For å øve mer, se oppgavesettet om median i Treningsleiren.
Oppgave 6 (4 poeng) Nettkode: E-4CTH
Marte er telefonselger. Hun har en fast grunnlønn per time. I tillegg får hun et fast beløp for hvert produkt hun selger.
En time solgte hun 2 produkter. Hun tjente da til sammen 170 kroner.
Den neste timen solgte hun 4 produkter. Denne timen tjente hun til sammen 220 kroner.
a)
Lag en grafisk framstilling som viser sammenhengen mellom hvor mange produkter Marte selger i løpet av en time, og hvor mye hun tjener denne timen.
Løsningsforslag a)
Jeg tenker
Her er det lurt å lage en
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi lager en graf. På
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
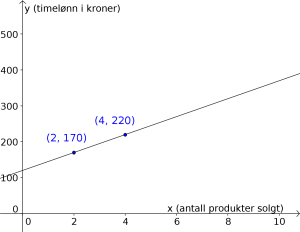
Her har vi passet på å sette på navn på aksene.
Svar:
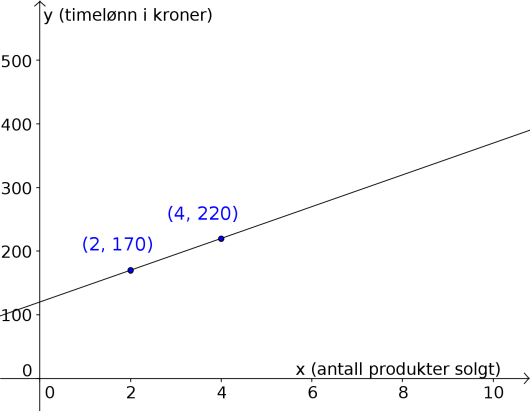
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere forklaringer og eksempler på koordinatsystemet, se artiklene Koordinatsystem, Rette linjer (linære funksjoner) og Grafen til en funksjon.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.
b)
Bruk den grafiske framstillingen til å bestemme Martes grunnlønn per time og det beløpet hun får for hvert produkt hun selger.
Løsningsforslag b)
Jeg tenker
Vi bruker grafen fra deloppgave a). Vi kan tolke grunnlønnen som
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Først finner vi grunnlønnen. Dette er lønnen som Marte får hvis hun ikke selger noen produkter. I den grafiske framstillingen vår representerer -aksen antall solgte produkter, og derfor vil vi finne ut hva timelønnen blir når . Vi ser at grafen krysser -aksen cirka der , så grunnlønnen til Marte er kroner.
Videre vil vi finne hvor mye Marte får i ekstra lønn per produkt hun selger. Dette tolkes som hvor mye vi stiger i -retning langs linjen hvis vi går i -retning, eller med andre ord, stigningstallet til linjen. Vi vet at Marte tjener kroner hvis hun selger produkter. Grunnlønnen hennes er kroner, og det betyr at de 2 produktene gav henne ekstra lønn. Det blir kroner per produkt.
Svar: Grunnlønnen til Marte er kroner per time, og hun får kroner ekstra per produkt hun selger.
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
For flere forklaringer og eksempler på lineære funksjoner, se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet lineære funksjoner i Treningsleiren.
c)
Hvor mange produkter må Marte selge i løpet av en time dersom hun skal tjene 370 kroner denne timen?
Løsningsforslag c)
Jeg tenker
Vi skal finne ut hva -verdien til den rette linjen er når -verdien er . Dette kan vi gjøre ved hjelp av den grafiske fremstillingen vår.
Vi bruker
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinat
Koordinatene til et punkt måles langs aksene i et koordinatsystem og forteller nøyaktig hvor vi finner punktet.
Eksempel: I punktet (1,3) er 1 førstekoordinat og 3 er andrekoordinat.
Se Koordinatsystem
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

Her ser vi at skjæringspunktet har koordinater . Det betyr at Marte må selge produkter for å få en timeslønn på kroner.
Alternativ løsning
Da merker vi oss at likningen til linjen vi har tegnet er . Vi vil finne ut når denne linjen krysser , og det gjør vi ved å finne den verdien for som passer inn i likningen Kort sagt gjør vi det ved å trekke fra på hver side av likhetstegnet, og deretter dividere med . Da får vi Vi regner ut at så Marte må selge produkter.
Svar: Marte må selge 10 produkter.
Mer om
Denne oppgaven er om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere forklaringer og eksempler se artiklene Grafisk løsning av likninger og Lineære likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Oppgave 7 (2 poeng) Nettkode: E-4CTR
a)
Forklar hva det vil si at en størrelse øker eksponentielt.
Løsningsforslag a)
Jeg tenker
En størrelse øker
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
En størrelse som øker
Eksponentialligning
En eksponentialligning er en ligning der én eller flere potenser har den ukjente i eksponenten.
Eksempel med som ukjent: eller
Man kan også forklare eksponentiell økning mer algebraisk. Størrelsen øker eksponentielt hvis den kan skrives på formen , der er et tall større enn . (Hvis hadde vært mindre enn , ville størrelsen ha avtatt eksponentielt.)
Svar: En størrelse øker eksponentielt hvis den hele tiden øker med en viss prosentandel.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere forklaringer og eksempler på eksponentialfunksjoner, se artikkelen Johannes viser eksponential- og logaritmefunksjoner.
For å øve mer, se oppgavesettet om eksponentialfunsksjoner i Treningsleiren.
b)
Nedenfor ser du tre ulike grafer. Hvilken eller hvilke av disse grafene illustrerer eksponentiell vekst? Begrunn svaret ditt.
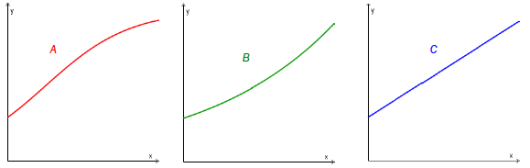
Løsningsforslag b)
Jeg tenker
Hvis en størrelse øker
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Graf øker mer og mer etter hvert som -verdien blir større. Det er dette vi er ute etter i eksponentiell vekst, og det er ingenting annet som tyder på at grafen ikke illustrerer eksponentiell vekst. Derfor er riktig svar.
Graf øker likt uansett hvor vi er på -aksen. Med eksponentiell vekst skal grafen øke mer og mer hele tiden, så illustrerer ikke eksponentiell vekst.
Svar: Graf er riktig, fordi den er den eneste av grafene som vokser mer og mer etter hvert som -verdien øker.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere forklaringer og eksempler på funksjoner og grafer, se artikkelen Hvorfor ser grafen ut som den gjør?.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
Oppgave 8 (2 poeng) Nettkode: E-4CTV
Sorter tallene i stigende rekkefølge
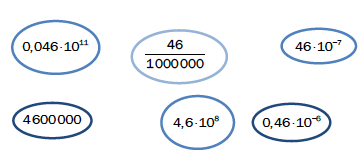
Løsningsforslag
Jeg tenker
Vi må finne en god måte å sammenligne tallene på. Her er nok det lureste å skrive om alle tallenet til
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Vi skriver om alle tallene til
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
:
Dette tallet er nesten på standardform. Det eneste som mangler er at tallet før tierpotensen skal være mellom og . Vi skriver som , og da får vi Her har vi brukt potensregelen som sier at vi kan legge sammen
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Grunntall
En potens består av et grunntall og en eksponent.
Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
:
Her bruker vi at (fordi det er nuller i , så ). Da kan vi skrive brøken som . Vi vil flytte tierpotensen opp fra nevneren, og da multipliserer vi med den omvendte potensen over og under brøkstreken. Vi får Her har vi brukt at for alle tall som er forskjellige fra . Nå er vi i samme situasjon som over, nemlig at tallet før tierpotensen ikke er mellom og . Derfor skriver vi som , og vi fårHer har vi brukt de samme reglene som i forrige tall, og at er det samme som .
: Som tidligere skriver vi som , og vi får
:
I dette tallet er det siffer i tillegg til det første, og de fem bakerste er . Derfor kan vi se med én gang at tallet kan skrives som . Alternativt kan vi se at tallet er med nuller bak, altså , og deretter gjøre som i de tidligere oppgavene.
: Dette tallet er allerede på standardform.
:
Vi skriver som . Da får vi
Disse tallene er det lett å sette opp i stigende rekkefølge. Jo høyere eksponenten er, jo større er tallet. Stigende rekkefølge med tallene på standardform erMed de opprinnelige tallene er rekkefølgen
Svar: Stigende rekkefølge med tallene på standardform er Med de opprinnelige tallene er rekkefølgen
Mer om
Denne oppgaven er om
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Desimaltall
Desimaltall er tall som inneholder komma.
Eksempel: 2,34 og 18,001
Sifrene som følger etter komma, kalles desimaler.
For flere forklaringer og eksempler på standardform, se artiklene Tall på standardform og Potenser med samme grunntall.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.
Oppgave 9 (3 poeng) Nettkode: E-4CTZ
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
| 5 | |||
| 15 | |||
| 2 | 0,1 | ||
| 19 | |||
| 20 |
Ole har undersøkt hvor mange land hver elev i en 2P-gruppe har besøkt. Han har satt opp en tabell. Ovenfor ser du noen av tallene i tabellen.
Tegn av tabellen, gjør beregninger, og fyll inn tallene som mangler.
Løsningsforslag
Jeg tenker
Her må vi huske på definisjonene av
Frekvens
Frekvensen er resultatet av å dele det totale antallet ganger en hendelse intereffer i løpet av et bestemt tidsintervall på intervallets lengde.
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Frekvens
Frekvens er antall ganger et svaralternativ eller en observasjon finnes i en datasamling. Vi finner fekvensen ved å telle opp hvor mange ganger en og samme data inntreffer.
Se frekvenstabell
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Det første vi gjør er å skrive av tabellen slik den er.
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Det kan være lurt å fylle inn tabellen ovenfra og ned, og vi starter med den relative frekvensen for . Vi skal altså finne ut hvor stor andel av elevene som har besøkt mellom og land. Frekvensen for intervallet er , så elever faller innenfor denne kategorien. Det neste vi må vite er antall elever i klassen. Det kan vi gjøre ved å se på den kumulative frekvensen for . Den er , og det betyr at det er elever som har besøkt land eller færre. Men ingen elever har besøkt mer enn land, så da må det være totalt elever i klassen! Vi vet at av disse er i intervallet , og da er den relative frekvensen til lik . Vi skriver dette inn i tabellen.
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Videre finner vi den kumulative frekvensen for , altså antall elever i klassen som har besøkt mellom og land. Det vet vi allerede er , så det er den kumulative frekvensen. (Dette stemmer mer generelt: Frekvens og kumulativ frekvens er lik i det første intervallet.) Vi fyller inn.
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Nå begynner vi på andre rad. Vi ser at den kumulative frekvensen for er , så elever har besøkt opp til land. Fra første rad ved vi at av disse har besøkt land eller færre, og da står vi igjen med elever i intervallet . Dermed er frekvensen til intervallet lik . Vi fant ut over at det er elever i klassen, og da blir relativ frekvens lik . Vi fyller inn.
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Vi starter på tredje rad, med den kumulative frekvensen til intervallet . Vi ser fra tabellen at det er elever som har besøkt opp til land, og elever har besøkt mellom og land. Da må den kumulative frekvensen til være .
Vi fortsetter med fjerde rad. Kumulativ frekvens øker fra til fra til , så det er elever i intervallet . Det utgjør av alle elevene. Vi fyller inn i henholdsvis “frekvens”- og “relativ frekvens”-ruten.
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Den siste raden tar vi på samme måte som forrige. Kumulativ frekvens øker med , så frekvensen er . Dette utgjør av klassen. Den ferdige utfylte tabellen er vist nedenfor.
Svar:
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
Mer om
Denne oppgaven er om
Frekvens
Frekvensen er resultatet av å dele det totale antallet ganger en hendelse intereffer i løpet av et bestemt tidsintervall på intervallets lengde.
Kumulativ frekvens

Den kumulative frekvensen til en verdi i et datamateriale sier hvor stor andel av datamaterialet som har denne verdien eller lavere.
Vi finner den kumulative frekvensen ved å summere alle frekvensene opp til og med den aktuelle verdien.
Eksempel: Se bildet. Her vil den kumulative frekvensen for 2 eller færre kjøpte lunsjer være 6 + 21 + 15 = 42. Det vil si at det er 42 personer som har kjøpt 2 eller færre lunsjer.
Relativ frekvens
Antall observasjoner av en spesiell hendelse dividert på antall observasjoner.
Eksempel: Dersom du kaster en terning 40 ganger og får 4 seksere, er den relative frekvensen av seksere 4/40 = 0,1.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere forklaringer og eksempler på frekvenstabell, se artikkelen Frekvenstabell.
DEL 2 Med hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4CUC
Ved en skole er det 440 elever. Elevene ble spurt om hvor ofte de bruker sykkelhjelm. Tabellen nedenfor viser resultatene.
| Alltid | 88 |
| Nesten alltid | 176 |
| Noen ganger | 110 |
| Aldri | 22 |
| Sykler ikke | 44 |
Bruk regneark til å lage et sektordiagram som illustrerer opplysningene i tabellen ovenfor. Det skal gå klart fram av diagrammet hvor mange prosent hver sektor utgjør.
Løsningsforslag
Jeg tenker
Her kan vi bruke regneark i Excel før vi lager
Sektordiagram
Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
Vi bruker Excel. Det første vi gjør er å skrive av tabellen.
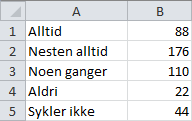
Deretter markerer vi tabellen, velger «Sett inn»-menyen og klikker på «Sektor». Der velger vi et passende diagram.
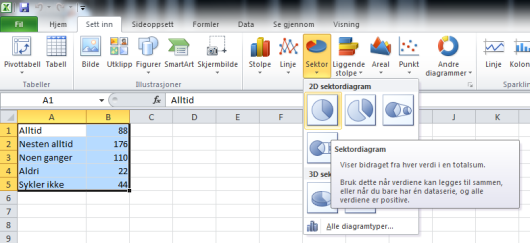
Vi får følgende diagram.
Det skal gå klart fram hvor mange prosent hver sektor utgjør. For å få til dette, høyreklikker vi på diagrammet og velger «Legg til dataetiketter». Så høyreklikker vi igjen og velger «Formater dataetiketter».
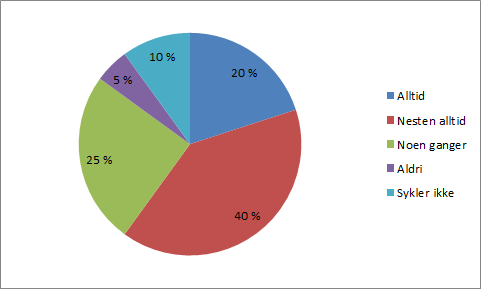
Det resulterende diagrammet er vist under.
Svar:
Mer om
Denne oppgaven er om
Sektordiagram

Et sektordiagram, også kalt kakediagram, viser prosentmessig fordeling av data eller klasser av data.
For flere forklaringer og eksempler på sektordiagrammer, se artikkelen Sektordiagram.
For å øve mer, se oppgavesettet om sektordiagram i Treningsleiren.
Oppgave 2 (3 poeng) Nettkode: E-4CUE
Hans og Grete går til Høgfjell hver dag. Nedenfor ser du hvor mange minutter Hans har brukt på hver tur de to siste ukene.
25 30 26 24 32 25 27 30 28 31 24 35 32 33
a)
Bestem gjennomsnitt og standardavvik for datamaterialet.
Løsningsforslag a)
Jeg tenker
Vi kan bruke et regneark for å finne
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Vi legger inn all informasjonen i Excel.
Først regner vi ut
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Tilsvarende finner vi
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Vi bruker fordi vi vil regne ut standardavviket for hele datasettet. Hvis vi hadde brukt , ville vi fått estimerte verdier basert på utvalg. Regnearket ser nå slik ut.
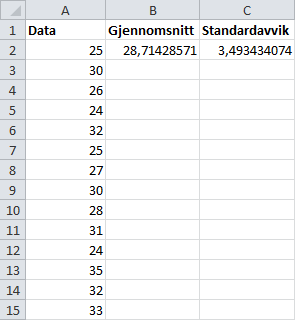
Vi ser at gjennomsnittet er cirka , mens standardavviket er cirka .
Svar: Gjennomsnittet er cirka , og standardavviket er cirka .
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
For flere forklaringer og eksempler på gjennomsnitt, se artiklene Gjennomsnitt, median og typetall og Varians og standardavvik.
For å øve mer, se oppgavesettet om gjennomsnitt i Treningsleiren.
b)
Grete har i gjennomsnitt brukt like lang tid som Hans per tur de siste 14 dagene, men standardavviket hennes er 1,2.
Hva kan du ut fra dette si om tidene Grete har brukt på turene, sammenliknet med tidene Hans har brukt?
Løsningsforslag b)
Jeg tenker
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Både Hans og Grete har i gjennomsnitt gått på cirka minutter.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Svar: Gåtidene til Hans varierer mer enn Gretes gåtider.
Mer om
Denne oppgaven er om
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Standardavvik
Standardavviket er kvadratroten av variansen. Dette er på en måte et forventet avvik fra gjennomsnittet.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
For flere forklaringer og eksempler på statistikk, se artikkelen Varians og standardavvik.
Oppgave 3 (6 poeng) Nettkode: E-4CUI

Funksjonen gitt ved
viser hvor mange grader sola stod over horisonten timer etter midnatt i Bergen 21. juni 2015.
a)
Bruk graftegner til å tegne grafen til .
Løsningsforslag a)
Jeg tenker:
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
i «Skriv inn»-vinduet. Vi må tilpasse aksene slik at vi ser hele grafen, og vi må sette på passende navn på
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Svar:
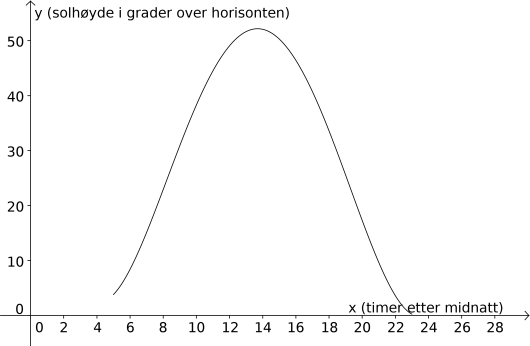
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere forklaringer og eksempler se artikkelen Typer av funksjoner og Hvorfor ser grafen ut som den gjør?.
For å øve mer, se oppgavesettet om grafisk fremstilling i Treningsleiren.
b)
Hvor mange grader stod sola over horisonten da den var på sitt høyeste?
Løsningsforslag b)
Jeg tenker
Solen står høyest der grafen har sitt
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Vi skal finne ut når solen stod høyest på himmelen, og det vil være der grafen når sitt høyeste punkt. Vi kan finne
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
i «Skriv inn»-vinduet.

Koordinatene til toppunktet er . Det betyr at solen var grader over horisonten timer etter midnatt, og det var det høyeste den kom.
Svar: grader.
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Ekstremalpunkter
Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
For flere forklaringer og eksempler se artikkelen om Topp- og bunnpunkter.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleiren.
Visste du at
Det finnes mange måter å regne ut toppunkter (og bunnpunkter) til en funksjon på. Man kan gjøre det ved regning ved hjelp av det som heter derivasjon, som går ut på å finne den momentane vekstfarten til funksjonen, og se på når denne vekstfarten blir . Eventuelt kan man finne tilnærminger til ekstremalpunktene ved hjelp av en datamaskin, og det er denne metoden som oftest brukes når funksjonen ikke er en enkel funksjon. Én metode man kan bruke på datamaskinen, er å se på funksjonsverdier i mange punkter, og se når den er høyest. I denne oppgaven kunne vi i så fall ha delt opp intervallet inn i deler (vi vil ofte ha veldig mange funksjonsverdier, eller sampler, når vi skal gjøre slike beregninger). Videre kunne vi satt alle disse -verdiene inn i funksjonen , og deretter plukke ut den høyeste verdien. Dette gjør vi åpenbart ikke for hånd, men det er relativt enkelt på datamaskin. Hvis en er kyndig i programmering, kan det være en god øvelse i både programmering og matematikk å implementere et slikt program.
c)
Når stod sola 20 grader over horisonten?
Løsningsforslag c)
Jeg tenker
Her kan vi bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi vil finne ut hva skal være for at . Det gjør vi ved å finne
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
i «Skriv inn»-vinduet, og deretter bruke skjæringsverktøyet til å finne skjæringspunktene.
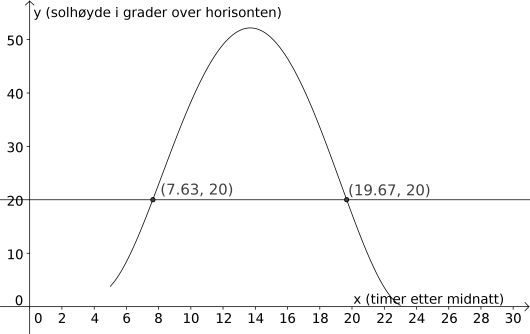
Her ser vi at skjæringspunktene har koordinater og . Det betyr at og timer etter midnatt, så var solen grader over horisonten. Det tilsvarer henholdsvis cirka klokken og .
Svar: og timer etter midnatt, eller cirka klokken og .
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Andregradslikning
En likning hvor x opptrer i andre potens. Vi kan alltid skrive en slik likning på formen:
Likningen kan løses ved hjelp av abc-formelen.
For flere forklaringer og eksempler Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Visste du at
I denne oppgaven har vi funnet hva skulle være for at . Dette er nøyaktig det samme som å løse ligningenunder betingelsen . Dette er en ganske komplisert ligning, og vi løste den på en veldig enkel måte grafisk. GeoGebras innebygde metoder for å finne skjæringspunkter kalles for numeriske metoder, og de er brukt for å løse mange typer vanskelige ligninger. Det finnes ligninger som er umulige å løse ved regning, enten praktisk umulig eller faktisk teoretisk umulig(!), og da må man ty til slike numeriske metoder.
d)
Hvor mange grader steg sola i gjennomsnitt per time fra klokka 05.00 til klokka 12.00?
Løsningsforslag d)
Jeg tenker
Gjennomsnittlig stigning mellom to punkter kan vi finne ved å se på
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Vi kan gjøre dette både grafisk og ved regning. Vi viser her ved regning, mens i alternativ løsning viser vi det grafisk.
Klokken var solen grader over horisonten (fordi er timer etter midnatt). Vi kan regne ut hva dette tallet er ved å skrive
i «Skriv inn»-vinduet. Da får vi . Klokken var solen grader over horisonten. Solen har dermed økt fra grader til grader på timer; det gir en gjennomsnittlig økning på grader per time.
Alternativ løsning
Vi kan også løse oppgaven grafisk ved å finne stigningstallet til den rette linjen mellom punktene og. Først skriver vi inn punktene i GeoGebra-filen, og deretter lager vi en rett linje mellom dem. Vi høyreklikker på linjen og velger «Likning » for å få likningen på en mer kjent form.
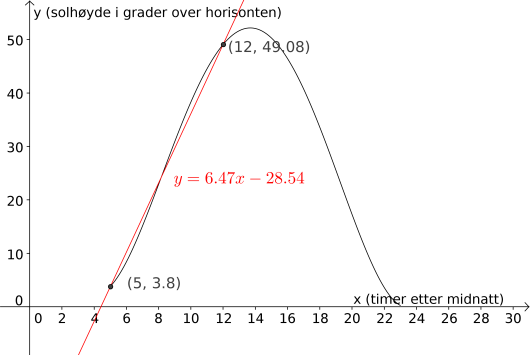
Her ser vi at stigningstallet til linjen er , og da er dette gjennomsnittlig stigning per time. Det var det samme som vi fikk i sted.
Svar: Cirka grader per time.
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Gjennomsnitt
Gjennomsnitt er en middelverdi av alle dataene.
Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data
Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1)
2) antall data er 4.
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
Statistikk
Statistikk dreier seg om innsamling og bearbeiding av data eller informasjon. Målet med statistikk er å presentere og gjøre beregninger på datamaterialet slik at det kan gi god og sann informasjon og være grunnlag for vurderinger.
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
For flere forklaringer og eksempler på lineære funksjoner, se artikkelen Rette linjer.
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.
Oppgave 4 (6 poeng) Nettkode: E-4CUP
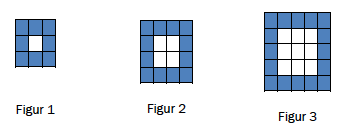
Tenk deg at du skal lage figurer av blå og hvite rektangler som vist ovenfor.
a)
Skriv av tabellen nedenfor, og fyll den ut.
| Figur | Antall hvite rektangler | Antall blå rektangler | Antall rektangler totalt |
| 1 | 1 | 8 | 9 |
| 2 | 4 | ||
| 3 | |||
| 4 | |||
| n |
Løsningsforslag a)
Jeg tenker
Hver figur har et stort hvitt
Kvadrat
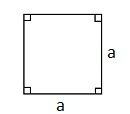
En firkant der alle sider er like lange og alle vinkler 90°.
Det aller første vi gjør er å skrive av tabellen slik den står.
Det første vi gjør er å skrive av tabellen slik den er.
| Figur | Antall hvite rektangler | Antall blå rektangler | Antall rektangler totalt |
Vi vil fylle ut rad nummer . Da teller vi antall blå rektangler i Figur , og det blir . Det hvite rektangler i figuren, og da blir det totale antallet rektangler lik . På tilsvarende måte teller vi at det er hvite rektangler i Figur , blå og totalt. Vi fyller dette inn i tabellen vår.
| Figur | Antall hvite rektangler | Antall blå rektangler | Antall rektangler totalt |
Når vi skal finne ut hva som skal stå i rad , kan vi ikke lenger telle antall kvadrater. Det vi kan (og skal) gjøre, er å se på mønsteret som figurene er bygget etter. I Figur er det hvitt rektangel, i Figur er det hvite rektangler, og i Figur er det hvite rektangler. Vi ser dette fordi de hvite rektanglene danner et stort rektangel i midten. I Figur skal det derfor være hvite rektangler i midten. Nå kunne vi begynt å regne ut antallet blå rektangler, men det vil være lettere å regne ut antall rektangler totalt først. Vi ser nemlig at rektanglene i hver figur danner et stort rektangel med lik bredde som høyde, målt i antall rektangler. Figur er rektangler i høyden og i bredden, Figur er rektangler i høyden og i bredden, og Figur er i høyden og i bredden. Derfor skal Figur være rektangler i høyden og i bredden, som gir et totalt antall rektangler på . Vi vet at av disse er hvite, og da må av dem være blå. Vi fyller ut.
| Figur | Antall hvite rektangler | Antall blå rektangler | Antall rektangler totalt |
Så skal vi fylle ut den siste raden. Det vanskelige arbeidet gjorde vi faktisk da vi fant ut systemet i rad
. Vi ser at i Figur , så må det være hvite rektangler, fordi det er et stort hvitt rektangel med bredde og høyde inne i figuren. Totalt må det være rektangler, fordi hele figuren er et rektangel med bredde og høyde . Da står vi igjen med blå rektangler. Den ferdig utfylte tabellen er vist under.
Svar:
| Figur | Antall hvite rektangler | Antall blå rektangler | Antall rektangler totalt |
Mer om
Denne oppgaven er om
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.
Eksempel: rutetabell for buss, resultatliste for skirenn
Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
For flere forklaringer og eksempler på faktorisering, se artikkelen Faktorisering av andregradsuttrykk.
b)
Hvor mange hvite rektangler trenger du dersom du skal lage en figur med totalt 81 rektangler?
Løsningsforslag b)
Jeg tenker
Her bruker vi det samme systemet som vi fant i deloppgave a).
I Figur er det totalt eller rektangler totalt. I vår figur er det rektangler; det betyr at må være det samme som , så eller . Dermed er det Figur som har 81 rektangler. Dette kunne vi også funnet grafisk ved å finne skjæringspunktet mellom funksjonen og linjen , som vist under.

Videre vet vi fra tabellen vår at det skal være hvite rektangler i Figur , og det betyr at det skal være hvite rektangler i Figur . Derfor er svaret .
Svar: hvite rektangler.
Mer om
Denne oppgaven er om
Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere forklaringer og eksempler på andregradsgrafer, se artikkelen Funksjonsgrafer for andregradsfunksjoner.
c)
Hvor mange blå rektangler trenger du dersom du skal lage en figur med totalt 1 296 rektangler?
Løsningsforslag c)
Jeg tenker
Her skal vi gjøre cirka det samme som i deloppgave b).
Som i forrige oppgave, starter vi med å finne ut hvilken figur som har rektangler totalt. Figur har totalt rektangler, og vi vil finne ut hva skal være for at dette skal bli . Dette kan vi gjøre ved å prøve oss fram, eller løse ligningen grafisk som i forrige oppgave.

Fra figuren over ser vi at det er Figur som har rektangler. Vi vet at Figur har blå rektangler, og da vil Figur ha blå rektangler.
Svar: blå rektangler.
Mer om
Denne oppgaven er om
Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:
Omkrets:
Polynom
Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.
Eksempler: og .
Polynomlikning
En likning der bare summer og produkter av en eller flere ukjente og konstanter forekommer.
For flere forklaringer og eksempler på andregradslikninger, se artikkelen abc-formelen.
Oppgave 5 (6 poeng) Nettkode: E-4CUT
En bedrift slapp ut 20 000 tonn CO2 i 2015. Myndighetene krever at bedriften reduserer utslippet av CO2 med 8 % hvert år de neste 10 årene.
a)
Bruk regneark til å lage en oversikt som viser antall tonn CO2 bedriften kan slippe ut hvert år de neste 10 årene.
Løsningsforslag a)
Jeg tenker
Her skal vi sette opp en tabell som viser antall tonn CO bedriftene kan slippe ut hvert år.
Vi setter opp en tabell vi skal fylle ut. Venstre side viser årstallet, mens høyre side viser antall tonn tillatte CO-utslipp. I slapp bedriften ut tonn, og vi skriver inn dette som vårt utgangspunkt. I skulle utslippet sunket med . Det gir en
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
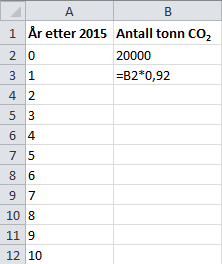
For skal bedriften senke utslippene ytterligere; derfor skal vi skrive
på neste linje igjen. Slik fortsetter vi helt til slutten av tabellen. Vi kan gjøre det raskt ved å markere rutene vi allerede har skrevet inn, og deretter dra nedover. Resultatet er vist under.
Svar:
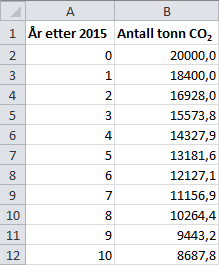
Mer om
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.
Eksempel: rutetabell for buss, resultatliste for skirenn
For flere forklaringer og eksempler på prosentregning, se lynkurset Prosent.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
b)
Hvor mange prosent vil bedriften totalt ha redusert utslippet med i løpet av denne perioden?
Løsningsforslag b)
Jeg tenker:
Dette kan vi gjøre ved å bruke tabellen fra deloppgave a), og regne ut.
Etter år har bedriften lov til å slippe ut tonn CO. Det er en reduksjon på tonn. Av er dette så reduksjonen er på totalt .
Alternativ løsning
Vekstfaktoren er .
Vi har derfor at
Dette gir oss at
Svar: Cirka
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
For flere forklaringer og eksempler på prosent, se artikkelen Regneregeler.
For å øve mer, se oppgavesettet om prosentregning i Treningsleiren.
c)
En annen bedrift slapp ut 30 000 tonn CO2 i 2015. Myndighetene krever at denne bedriften halverer utslippet i løpet av 5 år. Bedriften vil oppfylle myndighetenes krav ved å redusere utslippet av CO2 med en fast prosentsats hvert år framover.
Bestem denne prosentsatsen.
Løsningsforslag c)
Jeg tenker:
Her er det lurt å sette opp en modell for det tillatte utslippet.
La oss si at bedriften reduserer utslippet med en vekstfaktor på . (For eksempel, hvis , så må bedriften kutte utslippene med prosent hvert år.) Etter ett år er tillatt utslipp da lik ; etter to år er det , og så videre. Modellen vår for det tillatte utslippet er etter år. Etter 5 år er tillatt utslipp lik . Vi vil at dette tallet skal være halvparten av utslippene i utgangspunktet, og da må vi ha at Dette er en likning vi skal løse for . Vi kan gjøre det grafisk og med CAS, eller med regning. Vi gjør det sistnevnte, for det går relativt fort. Det eneste vi gjør er å opphøye begge sidene i . Da får vi Potensreglene sier at . Derfor har vi at Det betyr at den årlige prosentsatsen er cirka .
Alternativ løsning
Vi kunne også ha løst likningen grafisk slik bildet under illustrerer.
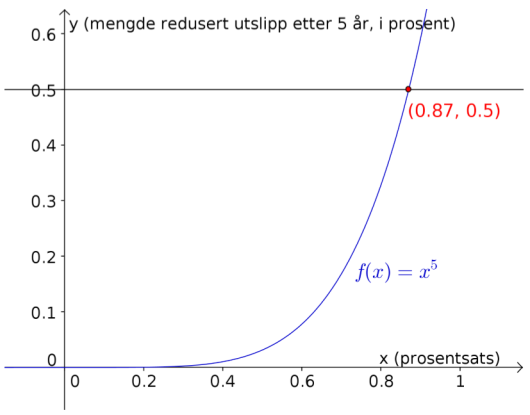
Svar: Cirka .
Mer om:
Denne oppgaven er om
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
For flere forklaringer og eksempler på matematiske modeller, se artikkelen Å lage en matematisk modell. Se ellers artiklene Rask gjennomgang av regneregler for potens og røtter og Grafisk løsning av likninger.
For å øve mer, se oppgavesettet om skjæringspunkter i Treningsleiren.
Oppgave 6 (5 poeng) Nettkode: E-4CV1
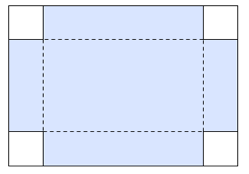
Tenk deg at du har et stykke papp med form som et rektangel. Rektangelet er 20 cm langt og 14 cm bredt. I hvert hjørne av rektangelet skal du klippe bort et kvadrat. De fire kvadratene skal være like store. Du skal så brette langs de stiplede linjene og lage en eske (uten lokk).
a)
Gjør beregninger, tegn av, og fyll ut tabellen nedenfor.
| Lengden av hver side i kvadratene som klippes bort |
Lengden av esken |
Bredden av esken |
Høyden av esken |
Volumet av esken |
| 4 cm | 288 cm3 | |||
| 3 cm | 8 cm | |||
| 2,5 cm | ||||
| x cm |
Løsningsforslag a)
Jeg tenker
Den stiplede firkanten i midten av tegningen danner bunnen av esken, og de fire utstikkende firkantene danner sidene.
Det første vi gjør er å skrive av tabellen slik den er.
|
Lengden av |
Lengden av |
Bredden av esken |
Høyden av esken |
Volumet av esken |
Vi starter med den første linjen. Vi skal finne lengden, bredden og høyden av boksen når vi klipper bort kvadrater med sidelengde i hver av hjørnene. Bunnen av esken er den stiplede firkanten markert i tegningen, og lengden av esken vil være lengden av de horisontale stiplede stripene. Vi vet at hele papprektangelet er langt, og hvis vi klipper bort
i hvert hjørne, står vi igjen med , og dette er lengden av boksen. Tilsvarende er papprektangelet bredt, og etter klippingen står vi igjen med . Høyden til rektangelet er sidelengden i kvadratet vi klipper bort, altså . Figuren under illustrerer situasjonen. (Målene på tegningen står ikke til de faktiske proposjonene.)
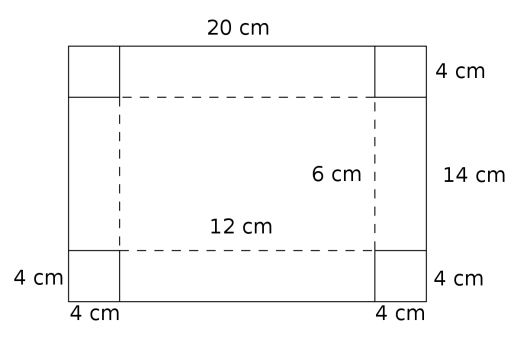
Dette kan vi fylle inn i tabellen vår.
| Lengden av hver side i kvadratene som klippes bort |
Lengden av esken |
Bredden av esken |
Høyden av esken |
Volumet av esken |
Volumet i en boks med lengde , bredde og høyde er . I vårt tilfelle er , og, og vi kan merke oss at akkurat som det står i tabellen.
Vi går videre til neste rad, der vi skal klippe bort kvadrater med sidelengde . Lengden av papprektangelet er fremdeles , så da blir lengden av esken lik . Tilsvarende blir bredden , slik som det står i tabellen. Høyden er , og da blir volumet
På samme vis regner vi ut raden med . Lengden av esken blir da , bredden blir og høyden er . Volumet av esken er dermed
Vi fyller dette inn i tabellen.
| Lengden av hver side i kvadratene som klippes bort |
Lengden av |
Bredden av esken |
Høyden av esken |
Volumet av esken |
Til slutt skal vi finne dimensjonene til eksen når vi klipper bort kvadratene med sidelengde . Vi gjør helt det samme som tidligere. Hvis vi klipper bort to kvadrater med sidelengde fra papprektangelet med lengde , står vi igjen med , og dette er lengden til esken. Bredden blir helt tilsvarende , og høyden er . Volumet til esken blirHvis vi løser opp parentesene, får vi . Den ferdig utfylte tabellen er vist under.
Svar:
| Lengden av hver side i kvadratene som klippes bort |
Lengden av esken |
Bredden av esken |
Høyden av esken |
Volumet av esken |
Mer om
Denne oppgaven er om
Tabell

Tabeller brukes til å organisere informasjon, ofte i kolonner og rader.
Eksempel: rutetabell for buss, resultatliste for skirenn
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
For flere forklaringer og eksempler på areal og volum, se artikkelen Geometri - areal og volum.
b)
Bruk graftegner til å bestemme hvor lang hver side i kvadratene som klippes bort, må være for at volumet av esken skal bli størst mulig.
Hvor stort blir volumet da?
Løsningsforslag b)
Jeg tenker
Vi har funnet
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.
La være
Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
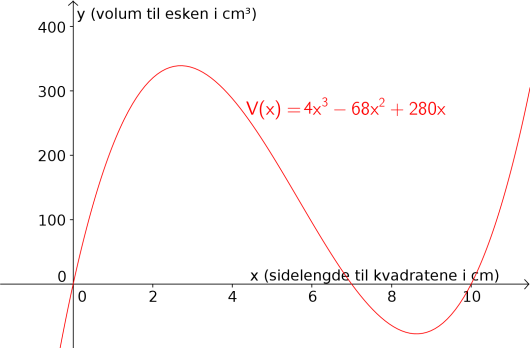
Vi vil finne ut når esken har størst volum, og det er der grafen til har et toppunkt. Vi finner
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
i «Skriv inn»-vinduet.
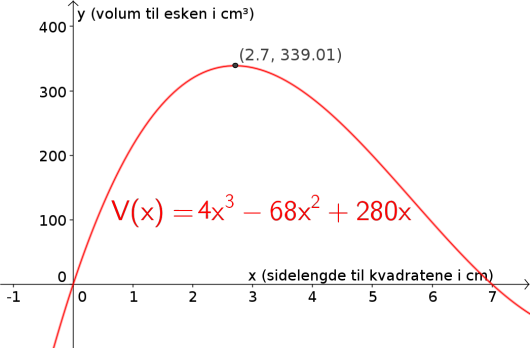
Her ser vi at toppunktet er . Det betyr at vi får det største volumet når vi klipper bort kvadrater med sidelengde ; da vil esken få et volum på cirka .
Svar: Det største volumet får vi når vi klipper bort kvadrater med sidelengde ; da vil esken få et volum på .
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Ekstremalpunkter
Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
For flere forklaringer og eksempler på grafer, se artikkelen Hvorfor ser grafen ut som den gjør?.
Oppgave 7 (8 poeng) Nettkode: E-4CV6
Ved havets overflate er lufttrykket ca. 1 000 hPa (hektopascal).
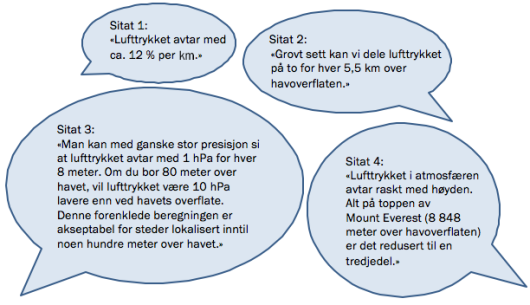
I denne oppgaven skal vi bruke sitater fra ulike nettsider og se på noen modeller for hvor stort luftrykket er x kilometer over havets overflate.
a)
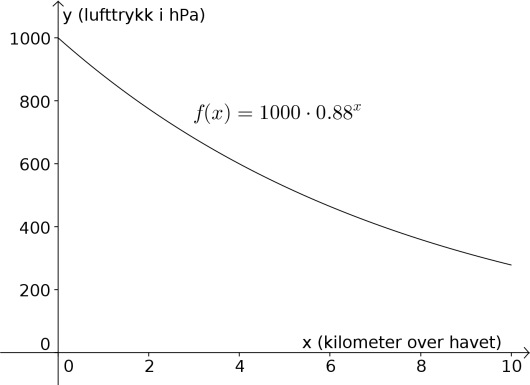
Forklar at vi ut fra sitat 1 kan sette opp en modell der
Tegn grafen til for
Løsningsforslag a)
Jeg tenker:
Sitat 1 sier at lufttrykket avtar med cirka per kilometer. Det er
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Hvis lufttrykket skal avta fra pHa med den første kilometeren over havet, vil lufttrykket én kilometer over havet være . (Det er fordi en reduksjon på gir en
Vekstfaktor
Er en prosentvis endring hvor vi ser på en økning eller en nedgang av en verdi.
Eksempel: en vekstfaktor på 1,15 betyr 15 % økning. Tilsvarende vil en vekstfaktor på 0,85 bety 15 % nedgang.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
i «Skriv inn»-vinduet. Vi drar til aksene slik at vi ser hele
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Svar: Modellen gir mening fordi lufttrykket synker med per kilometer, som er eksponentiell reduksjon med vekstfaktor .
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
For flere forklaringer og eksempler på potenser, se artikkelen Typer av funksjoner.
For å øve mer, se oppgavesettet om eksponentialfunksjoer i Treningsleiren.
b)
Forklar at sitat 2 gir tabellen nedenfor. Bruk regresjon, og vis at opplysningene i tabellen gir en modell som er tilnærmet lik modell . Gi denne modellen navnet .
Tegn grafen til for i samme koordinatsystem som grafen til .
| Høyde over havoverflaten (km) |
0 | 5,5 | 11 | 16,5 |
| Lufttrykk (hPa) | 1000 | 500 | 250 | 125 |
Løsningsforslag b)
Jeg tenker
Vi skal sjekke at tabellen passer med den beskrevne halveringen.
Ved havoverflaten er trykket hPa, og i følge sitatet skal trykket divideres med for hver vi beveger oss oppover. Det betyr at lufttrykket skal være hPa når vi er over havet, hPa når vi er over havet, og hPa når vi er over havet. Dette passer med tabellen.
Videre skal vi finne en modell for lufttrykket ved å bruke
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
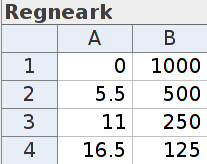
Vi markerer tabellen, høyreklikker og velger «Tabell med punkt» i «Lag»-menyen. Listen blir hetende Liste1. Nå skal vi lage en ny modell ved regresjon, og da må vi velge hvilken type funksjon vi skal gjøre regresjonen med. At lufttrykket halveres per antyder at en eksponentiell modell vil være passende. Derfor skriver vi
i «Skriv inn»-vinduet. Resultatet er vist under.
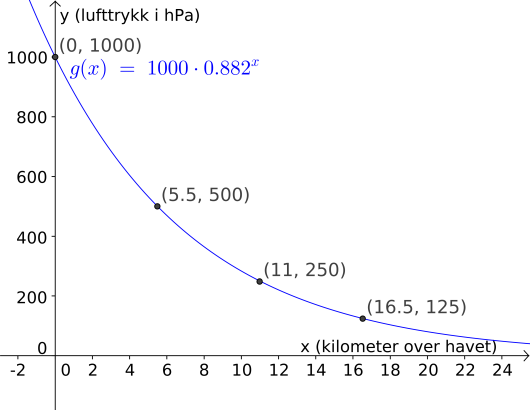
Hvis vi går på Innstillinger og velger desimaler under «Avrunding», så ser vi at den nye modellen er cirka altså nesten likt modellen fra forrige oppgave. Vi kan også se dette ved å tegne inn begge modellen i samme vindu, som vist under.
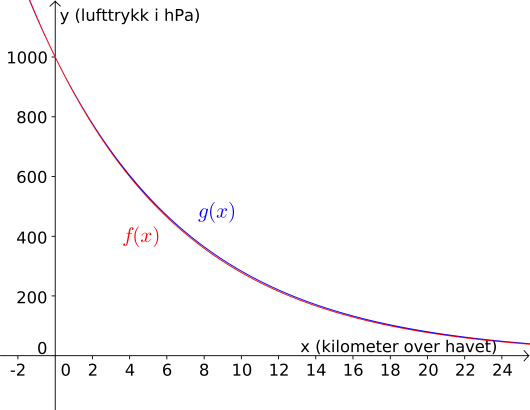
Svar: Tabellen passer med halvveringene beskrevet i sitatet. Den nye modellen er gitt ved (cirka) , som er nesten likt modellen fra forrige oppgave.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
For flere forklaringer og eksempler på regresjon, se artikkelen Regresjon: Hva betyr det at en kurve "passer til dataene"?.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.
c)
Bruk sitat 3 til å bestemme en modell . Tegn grafen til for i samme koordinatsystem som du har brukt tidligere i oppgaven.
Kommenter siste setning i sitat 3.
Løsningsforslag c)
Jeg tenker
Sitat sier at lufttrykket vil avta
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Sitat sier at lufttrykket vil avta like fort uansett hvor høyt oppe man er. Det betyr at lufttrykket er en
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Vi tegner dette inn i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
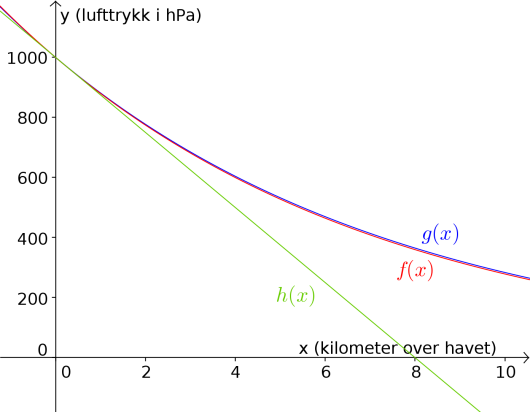
Den siste setningen i sitat 3 sier at modellen bare er gyldig inntil noen hundre meter over havet. Det kan vi se på grafene. Der er liten, så er ganske lik og , men minker usannsynlig fort i forhold til de andre når blir større. Etter hvert gir negativt lufttrykk, som ikke er mulig.
Svar: Modellen er .

Mer om
Denne oppgaven er om
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere forklaringer og eksempler på funksjoner, se artikkelen Rette linjer (lineære funksjoner).
For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleiren.
d)
Bruk hver av de tre modellene , og til å bestemme lufttrykket 8 848 meter over havoverflaten. Sammenlikn svarene du får, med sitat 4, og kommenter.
Løsningsforslag d)
Jeg tenker
Vi kan skrive som . Dermed skal vi evaluere de forskjellige funksjonene for , altså finne
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Vi finner funksjonsverdiene , og . Det kan vi gjøre enkelt ved å skrive det direkte inn i
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
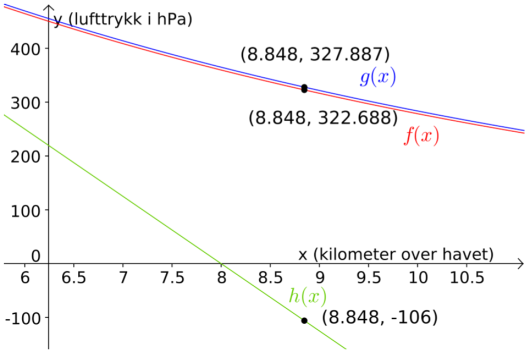
Her ser vi at , og . Ved Mount Everest skal lufttrykket være cirka én tredjedel av hPa, altså cirka hPa. De to
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Svar: Vi har , og . Det egentlige lufttrykket skal være rundt hPa. Sitat sier at den lineære modellen kun skal benyttes på steder som er inntil noen hundre meter over havet, og da gir -verdien mening.
Mer om
Denne oppgaven er om
Eksponentialfunksjon

En matematisk funksjon på formen ax. Funksjonen er et potensuttrykk der x er eksponenten.
Brukes mest om funksjonen ex.
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Matematisk modell
Matematiske modeller brukes ofte for å beskrive fenomener i naturen.
Matematisk modell: Betegner at man setter opp matematiske relasjoner mellom størrelser man er interessert i å analysere utviklingen av. Etter at man har laget modellen kan en benytte matematikk for å beregne hvordan fenomenet utvikler seg. Mange matematiske modeller har så kompliserte likninger at de ikke kan løses eksakt og man må da benytte numeriske metoder. Når man har funnet en matematisk løsning må svaret tolkes i forhold til fenomenet en ser på.
Dersom svaret som kom ut av modellen rimelig har man satt opp en brukbar modell? Hvis svaret er urimelig har man satt opp en lite brukbar modell.
For flere forklaringer og eksempler på matematiske modeller, se artikkelen Hva er matematisk modellering?.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.




