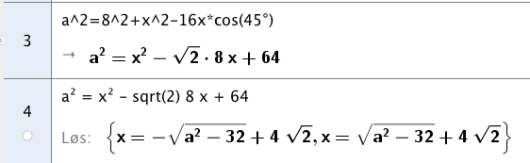Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2015 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Del 1 har 14 oppgaver. Del 2 har 6 oppgaver.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som «graftegner» og «CAS» skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Elbiler i kollektivfelt:
- http://e24.no/bil/fire-av-fem-kjoeretoey-i-kollektivfeltet-er-elbiler/23273402 (01.05.2015)
- Andre tegninger, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4BOI
Regn ut og skriv svaret på standardform
Oppgave 2 (2 poeng) Nettkode: E-4BON
Løs likningssystemet
Oppgave 3 (2 poeng) Nettkode: E-4BOP
Løs ulikheten
Oppgave 4 (2 poeng) Nettkode: E-4BOR
Regn ut og skriv svaret så enkelt som mulig
Oppgave 5 (2 poeng) Nettkode: E-4BOT
Likningen har løsningene og .
Bestem og .
Oppgave 6 (2 poeng) Nettkode: E-4BOV
Trekk sammen og skriv så enkelt som mulig
Oppgave 7 (2 poeng) Nettkode: E-4BOX
Skriv så enkelt som mulig
Oppgave 8 (2 poeng) Nettkode: E-4BOZ
Løs likningen
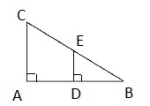
Oppgave 9 (2 poeng) Nettkode: E-4BP2
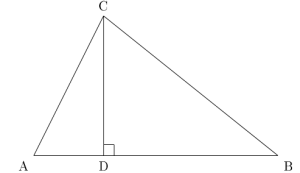
Bestem arealet av ovenfor.
Oppgave 10 (9 poeng) Nettkode: E-4BP4
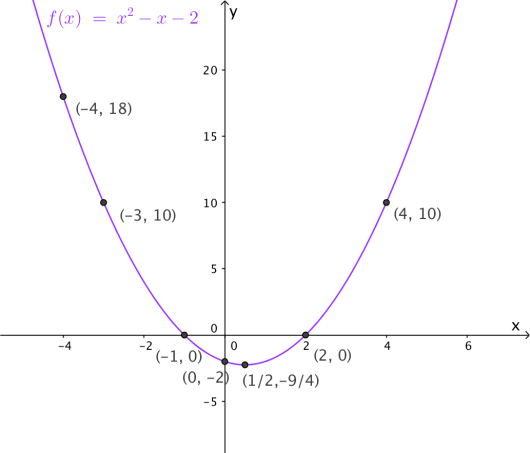
Funksjonen er gitt ved
a)
Bestem nullpunktene til .
b)
Vis at grafen til har bunnpunktet .
c)
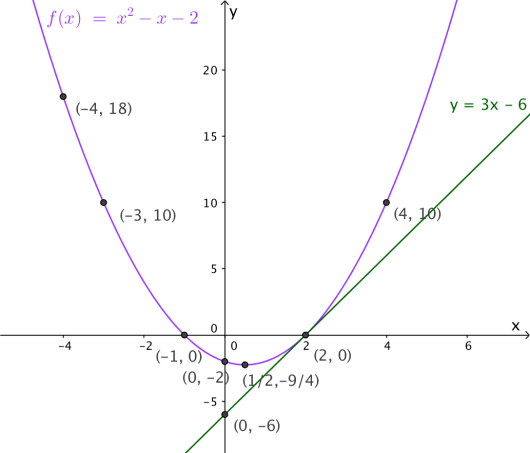
Bestem likningen for tangenten til grafen i punktet .
d)
En rett linje går gjennom punktet og er parallell med tangenten i oppgave c).
Bestem skjæringspunktene mellom linjen og grafen til ved regning.
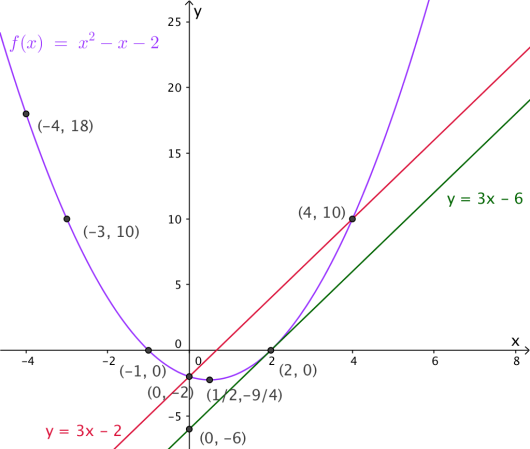
e)
Tegn grafen til , tangenten i oppgave c) og den rette linjen i oppgave d) i samme koordinatsystem.
Oppgave 11 (2 poeng) Nettkode: E-4BPA
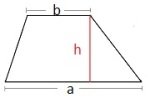
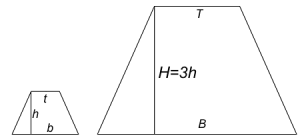
To trapes er formlike. Høyden i det minste trapeset er lik . Høyden i det største trapeset er lik . Det minste trapeset har areal .
Vis ved formelregning at det største trapeset har areal .
Oppgave 12 (4 poeng) Nettkode: E-4BPD
Forskere skal prøve ut en ny test for å avgjøre om en person er smittet av en bestemt sykdom.
Testen skal prøves ut på 360 personer. På forhånd vet forskerne at 60 av disse personene er smittet av sykdommen, mens resten ikke er smittet.
Det viser seg at 68 av personene tester positivt (det vil si at testen viser at de er smittet av sykdommen). Av disse 68 er det 10 personer som forskerne vet ikke er smittet.
a)
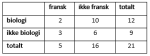
Tegn av og fyll ut krysstabellen nedenfor.
| Smittet | Ikke smittet | Sum | |
| Tester positivt |
|||
| Tester ikke positivt |
|||
| Sum |
b)
Bestem sannsynligheten for at en person som er smittet, tester positivt.
c)
Bestem sannsynligheten for at en person som tester positivt, ikke er smittet.
Oppgave 13 (2 poeng) Nettkode: E-4BPI
I er og .
Bestem .
Oppgave 14 (2 poeng) Nettkode: E-4BPL
Gitt slik at , og .
Bestem arealet av trekanten.
DEL 2 Med hjelpemidler
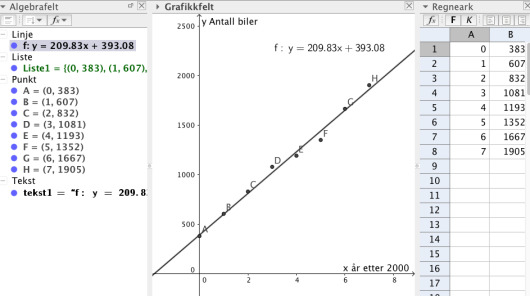
Oppgave 1 (3 poeng) Nettkode: E-4BPO
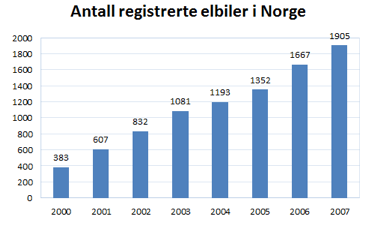
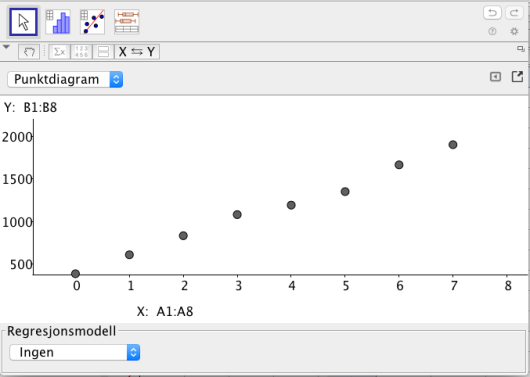
Diagrammet ovenfor viser antall registrerte elbiler i Norge hvert år fra år 2000 til år 2007. Antall registrerte elbiler økte tilnærmet lineært i denne perioden.
a)
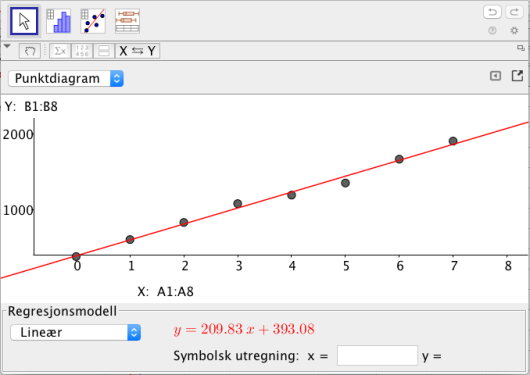
La være antall år etter år 2000. Bestem en funksjon som beskriver utviklingen.
b)
I 2008 var det 2 432 registrerte elbiler i Norge, i 2012 var det 9 580, og i 2014 var det 41 051.
Hvordan passer funksjonen fra oppgave a) med disse verdiene?
Oppgave 2 (3 poeng) Nettkode: E-4BPS
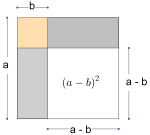
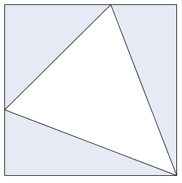
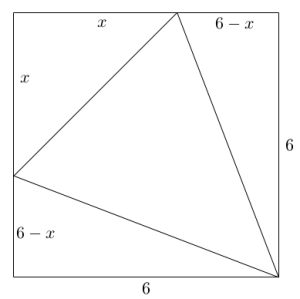
Et kvadrat har sider med lengde . Kvadratet er delt i tre blå og én hvit trekant. Se figuren ovenfor. Hver av de tre blå trekantene har like stort areal. Den hvite trekanten er likebeint.
Bestem et eksakt uttrykk for arealet av den hvite trekanten.
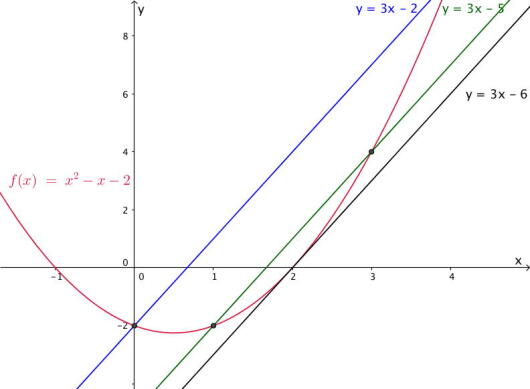
Oppgave 3 (4 poeng) Nettkode: E-4BPU
Funksjonen er gitt ved
a)
Bruk graftegner til å tegne
- grafen til
- en rett linje som går gjennom punktene og
- en rett linje som går gjennom punktene og
- tangenten til grafen til i punktet
b)
Bruk CAS til å vise at tangenten til grafen til i punktet er parallell med den rette linjen som går gjennom punktene og .
Oppgave 4 (2 poeng) Nettkode: E-4BPX
Et rektangel har areal og omkrets .
Hvor langt og hvor bredt er rektangelet?
Oppgave 5 (5 poeng) Nettkode: E-4BQ0
Nedenfor ser du overskrift og et sitat fra en artikkel på e.24.no/bil i 2014 etter at Statens vegvesen hadde foretatt trafikktellinger på en veistrekning.
a)
Vurder om sitatet fra artikkelen gir grunnlag for overskriften som er valgt.
b)
Anta at fire av fem kjøretøy i kollektivfeltet er elbiler, og at du står langs denne veistrekningen i telleperioden.
Bestem sannsynligheten for at nøyaktig ett av de tre neste kjøretøyene som passerer deg i kollektivfeltet, er elbiler.
c)
Bestem sannsynligheten for at minst to av de tre neste kjøretøyene som passerer deg i kollektivfeltet, er elbiler.
Oppgave 6 (7 poeng) Nettkode: E-4BQ4
Gitt slik at , og
a)
Bruk CAS til å bestemme lengden av eksakt.
b)
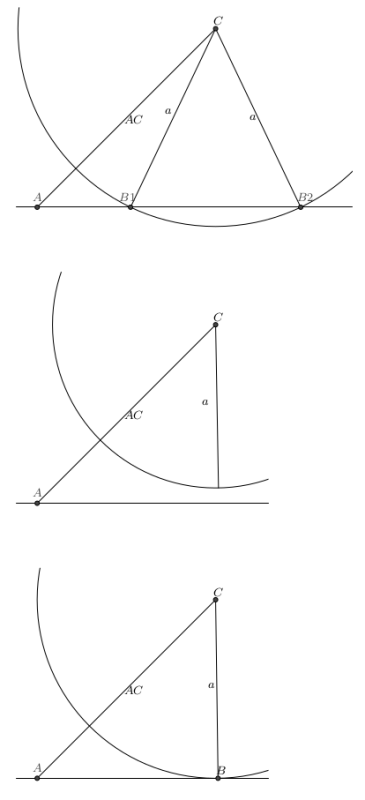
I resten av oppgaven setter vi .
Ved å velge ulike verdier for kan vi få to trekanter, én trekant eller ingen trekant.
Lag skisser som illustrerer dette.
c)
Sett .
Bruk CAS til å bestemme for hvilke verdier av likningen
- har to positive løsninger
- har én løsning
- ikke har løsning
Bruk eksakte verdier.
d)
Vurder om svarene i oppgave c) samsvarer med skissene du laget i oppgave b).