
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1013 2016 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 3 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.
Bruk av digitale verktøy som «graftegner» og «CAS» skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
- vurderer om svar er rimelige
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Tegninger, grafer og figurer: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-4BKM
Regn ut og skriv svaret på standardform
Løsningsforslag
Jeg tenker
Vi kan begynne med å skrive telleren og nevneren om til
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Dersom vi får både teller og nevner på standardform kan vi bruke regnereglene for potenser. I telleren gjør vi om desimaltallet til et heltall ved å multiplisere det med en tierpotens, da får vi . Nevneren kan vi skrive om, og får . Nå kan vi regne ut
For å regne ut brøken kan det være lurt å få nevner:
.
Da får vi videre at
Svar:
Mer om
Denne oppgaven handler om
Standardform
Et tall skrevet på formen ± a⋅10n der a er et tall mellom 1 og 10 og n er et heltall.
Eksempel:
Flere forklaringer og eksempler på hvordan man finner standardform og regner med tall på denne formen finner du i artikkelen Tall på standardform.
For å øve mer, se oppgavesettet om tall på standardform i Treningsleiren.
Oppgave 2 (3 poeng) Nettkode: E-4BKP

På tallinjen ovenfor er det merket av 12 punkter. Hvert av tallene nedenfor tilsvarer ett av punktene A – L på tallinjen.
Regn ut eller forklar hvor hvert av tallene skal plasseres.
1)
2)
3)
4)
5)
6)
Løsningsforslag
Jeg tenker
Her kan vi se
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Rot
Se Kvadratrot
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.
1) Dette er en potens. Vi vet at at
og får at
som tilsvarer F
2) Her har vi et produkt med en potens. Vi bruker at
og får at
som tilsvarer L
3) Dette er en logaritme. Vi begynner med å gjøre desimaltallet til en potens, da får vi og bruker at
slik at vi får
som tilsvarer B
4) Vi vet at en potens
og får at
. Vi vet at , må være litt større enn . Da kan det enten være I eller J, men og siden må det tilsvare I.
5) En rettvinklet trekant med en vinkel på er likebeint og katetene vil være like lange. Tangens er forholdet mellom motstående og hosliggende katet og derfor er tan som tilsvarer G.
6) er et kubikktall, og vi kan skrive og får som tilsvarer K.
Svar: 1 & F, 2 & L, 3 & B, 4 & I, 5 & G og 6 & K.
Mer om
Denne oppgaven handler om
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Potens
En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen , som leses x opphøyd i n-te.
Eksempel:
Trigonometri
Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.
For flere eksempler og forklaringer se lynkursene Potenser og røtter, Logaritmer og Trigonometri.
For å øve mer, se oppgavesettene, potenser og logaritmer i Treningsleiren.
Oppgave 3 (2 poeng) Nettkode: E-4BKW
Løs likningssystemet
Løsningsforslag
Jeg tenker
Vi kan bruke den andre likningen til å finne et uttrykk for og bruke dette uttrykket i den første likningen; altså kan vi bruke innsettingsmetoden, som er samme metode som substitusjonsmetoden.
Vi har likningssystemet
.
For å løse dette likningssystemet kan vi bruke innsettingsmetoden. Vi ser at i (2) kan vi finne et uttrykk for ,
Dette uttrykket kan vi sette inn for i (1) slik at vi får en likning med bare én ukjent.
Da får vi
og .
Vi setter inn for og i (2) for å finne . Da får vi og , så likningen har altså to løsninger.
Svar: eller .
Mer om
Denne oppgaven er om
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
For flere forklaringer og eksempler se artikkelen Likningssystemer og Substitusjonsmetoden.
For å øve mer, se oppgavesettet om likningssystemer i Treningsleiren.
Oppgave 4 (2 poeng) Nettkode: E-4BKY
Løs ulikheten
Løsningsforslag
Jeg tenker
Her har vi en andregradsulikhet og vi kan bruke abc-formelen til å finne nullpunktene til åFaktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
Vi begynner med å samle alle leddene på venstre side av ulikheten slik at vi får
Nå kan vi finne nullpunktene til ved hjelp av
abc-formelen
abc-formelen sier at en likning på formen har løsningene .
.
Vi setter inn i abc-formelen for å finn nullpunktene
Da får vi
og
Så vi kan skrive
.
Vi lager fortegnslinger for hver av faktorene ,
Fortegnssjemaet til :

Fra fortegnsskjema ser vi at for og for , så løsningsmengden blir .
Svar:
Mer om
Denne oppgaven handler om ulikheter.
Flere forklaringer og eksempler på hvordan man løser ulikheter finner du i lynkurset Ulikheter.
For å øve mer, se oppgavesettet om ulikheter av andre grad i Treningsleiren.
Oppgave 5 (3 poeng) Nettkode: E-4BL0
Regn ut og skriv svaret så enkelt som mulig
a)
Løsningsforslag a)
Jeg tenker
Vi har et produkt at to nesten like parenteser, der kun det andre leddet har motsatt fortegn i den andre parentesen, og da kan vi bruke
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Vi ser at dette er utrykk på formen der og . Ifølge konjugatsetningen er
. Dette bruker vi til å regne ut uttrykket vårt og får
Svar:
Mer om
Denne oppgaven handler om
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Flere forklaringer og eksempler finner du i artikkelen Kvadratsetningene.
For å øve mer, se oppgavesettet om kvadratsetningene i Treningsleiren.
b)
Løsningsforslag b)
Jeg tenker
For å regne ut kan vi
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
Svar:
Mer om
Denne oppgaven handler om
Kvadratrot
Kvadratrot har symbolet .
Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.
Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi . Det skrives .
Flere forklaringer og eksempler på hvordan finner du i lynkurset Potenser og røtter.
For å øve mer, se oppgavesettet om potenser i Treningsleiren.
Oppgave 6 (2 poeng) Nettkode: E-4BL4
Skriv så enkelt som mulig
Løsningsforslag
Jeg tenker
Vi har en brøk med andregradsuttrykk i teller og nevner. For å forkorte en brøk må vi ha samme faktor i
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.
Eksempel : . Tallet 7 er nevneren.
Vi skal faktorisere telleren og nevneren for seg. Vi begynner med telleren. Den minner oss om
Første kvadratsetning
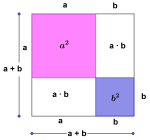
Første kvadratsetning sier at
.
Videre ser vi på nevneren. Vi kan begynne med å faktorisere
For den andre faktoren i nevneren ser det ut til at vi kan bruke
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Nå ser vi at telleren og nevneren har én fellesfaktor, slik at vi kan forkorte brøken:
Her kan vi ikke gjøre noe mer, og vi har skrevet brøken så enkelt som mulig.
Svar:
Mer om
Denne oppgaven handler om
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
Første kvadratsetning

Første kvadratsetning sier at
.
Konjugatsetningen

Konjugatsetningen kalles også tredje kvadratsetning:
.
Flere forklaringer og eksempler finner du i artikkelen Kvadratsetningene.
For å øve mer, se oppgavesettet om kvadratsetningene i Treningsleieren.
Oppgave 7 (2 poeng) Nettkode: E-4BL6
Løs likningen
Løsningsforslag
Jeg tenker
Vi har en
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
Vi begynner med å samle alle leddene med logaritmer på en på en side av likningen. Husk at for å må vi ha .
Nå han vi bruke at , og tar opphøyd i hver side av likningen.
Svar:
Mer om
Denne oppgaven handler om
Logaritme
Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.
Eksempel: log10(1000) = 3 ettersom 103 = 1000.
For flere forklaringer og eksempler se artikkelen Logaritmelikninger og for mer om regning med logaritmer se lynkurset Logaritmer.
For å øve mer, se oppgavesettet om likninger med logaritmefunksjoner i Treningsleiren.
Oppgave 8 (2 poeng) Nettkode: E-4BL8
Trekk sammen og skriv så enkelt som mulig
Løsningsforslag
Jeg tenker
For å trekke sammen brøker, må vi ha
Fellesnevner
Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.
Eksempel: , 42 er fellesnevner for disse to brøkene.
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi
Vi begynner med på faktorisere nevnere i brøkene for å finne fellesnevner.
Fellesnevneren her blir da .
Vi kan nå
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi
Vi ser nå at er felles faktoren i telleren og nevneren slik at vi kan forkorte brøken
Nevneren faktoriseres ytterligere og vi får
Svar:
Mer om
Denne oppgaven handler om
Faktorisering
Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.
Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3
Se også primtallsfaktorisering
Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
Utvide brøk
Å utvide en brøk betyr å multipliseres teller og nevner med samme tall. Brøken beholder samme verdi.
Eksempel: er utvidet til , fordi
For flere forklaringer og eksempler se artikkelen Parenteser og faktorisering og mer om brøker ser du i lynkurset Polynomdivisjon.
For å øve mer, se oppgavesettet om forenkling av sammensatte rasjonale uttrykk i Treningsleiren.
Oppgave 9 (4 poeng) Nettkode: E-4BLB

Snorre har seks blå og fire rosa ballonger. Han tar tilfeldig tre ballonger.
a)
Bestem sannsynligheten for at han tar tre blå ballonger.
Løsningsforslag a)
Jeg tenker
Hvis Snorre skal ta tre blå ballonger (BBB), må den første, den andre og den tredje ballongen han velger være blå. Vi skal derfor finne
Betinget sannsynlighet
Den betingede sannsynligheten er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.
.
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
Der er blå og rosa ballonger; totalt ballonger. Snorre skal trekke tre tilfeldige ballonger ut fra disse.
Sannsynligheten for at han trekker en blå ballong første gang, er
Vi antar nå at han trakk en blå ballong på første. Siden vi nå har fjernet én blå ballong er det nå 9 ballonger, og av disse er 5 blå. Da blir sannsynligheten for at han trekker en blå ballong andre gangen, lik
Hvis Snorre igjen trakk en blå ballong, er det nå ballonger igjen, hvorav er blå. Sannsynligheten for at han trekker en blå ballong tredje gang er da
Sannsynligheten for at Snorre trekker en blå ballong alle tre gangene, er sannsynligheten for at alle de tre hendelsene over har skjedd. Produktsetningen sier dermed at
Svar:
Mer om
Denne oppgaven handler om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
For flere eksempler og forklaringer se artikkelen Betinget sannsynlighet og produktsetningen i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om betinget sannsynlighet i Treningsleieren.
b)
Bestem sannsynligheten for at han tar minst én rosa ballong.
Løsningsforslag b)
Jeg tenker
Enten trekken Snorre tre blå ballonger, eller så trekker han minst én rosa ballong. Vi sier at de to hendelsene er
Komplement
Komplementet til A, betegnet med , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, .
Hendelsene at Snorre trekker tre blå ballonger og at han trekker minst én rosa er komplementære, og summen av sannsynligheten for to komplementære hendelser er , og vi må ha at
og dermed er
I deloppgave a) fant vi at , og da får vi
Svar:
Mer om
Denne oppgaven handler om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
For flere forklaringer og eksempler se artikkelen Sannsynlighet ved komplementære hendelser i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om utfallsrom i Treningsleieren.
c)
Bestem sannsynligheten for at han tar én rosa og to blå ballonger.
Løsningsforslag c)
Jeg tenker
Snorre kan trekke to blå og én rosa på flere måter. Vi kan finne sannsynligheten for de ulike måtene og bruke
Addisjonssetningen
Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.
For at Snorre skal trekke én rosa ballong og to blå, kan han enten
- trekke en rosa først, og deretter to blå,
- først trekke en blå, deretter en rosa, og til slutt en blå, eller
- trekke to blå og deretter en rosa.
Vi har altså hendelsene . NÅ kan vi regne ut sannsynligheten for hver av disse hendelsene.
Vi begynner med hendelsen . Vi begynner med ballonger, hvorav er rosa. Sannsynligheten for at den første ballongen er rosa er .
Når Snorre har trukket den rosa ballongen er det igjen, hvorav er blå. Sannsynligheten for at den neste ballongen er blå, blir da .
Før Snorre trekker den siste ballongen er det ballonger igjen, hvorav er blå. Da blir sannsynligheten for at den siste ballongen er blå, lik .
Totalt har vi dermed
Sannsynlighetene for de andre hendelsene regner vi ut på tilsvarende måte, og vi får at
og
Siden de tre hendelsene BBR, BRB og RBB er uavhengige, bruker vi addisjonssetningen og finner sannsynligheten for én rosa og to blå ballonger:
Svar:
Mer om
Denne oppgaven er om
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1.
Addisjonssetningen
Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.
For flere forklaringer og eksempler se artikkelen Addisjonssetningen i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om addisjonssetningen i Treningsleieren.
Oppgave 10 (3 poeng) Nettkode: E-4BLK
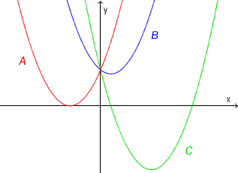
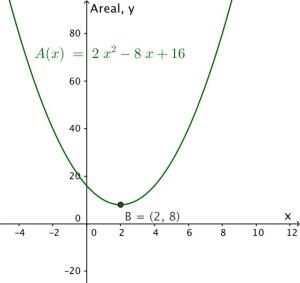
Funksjonene , og er gitt ved
I koordinatsystemet ovenfor ser du grafene til , og .
Hvilken graf er grafen til , hvilken graf er grafen til , og hvilken graf er grafen til ? Begrunn svarene dine.
Løsningsforslag
Jeg tenker
Vi ser at en ting som skiller de tre grafene, A,B og C fra hverandre er at de har forskjellig antall nullpunkter.
Et andregradsuttrykk har
- ingen nullpunkter (B) hvis og bare hvis
- ett nullpunkt (A) hvis og bare hvis
- to nullpunkter (C) hvis og bare hvis
Dette kan vi bruke til å bestemme hvilke funksjoner og grafer som hører sammen. Vi regner ut for , og :
Vi begynner med funksjonen :
Dette betyr at ikke har noen nullpunkter, og da må vi ha at B er grafen til .
Vi fortsetter med å se på :
Funksjonen har altså to nullpunkter, og dermed må grafen til være C.
Da må vi ha at grafen til er A, men vi sjekker for også:
har et nullpunkt, og dette stemmer med grafen A.
Alternativ
Vi kan finne bunnpunktene til funksjonene ved å derivere dem og finne når den deriverte er null. Da kan vi deretter sammenlikne med bunnpunktene til grafene.
Vi kan begynne med å se på hver av funksjonene:
Vi vil nå finne når og løser likningen
Funksjonen har bunnpunkt når .
Vi fortsetter med å se på funksjonen
og likningen
Dette gir at funksjonen har bunnpunkt når .
For den siste funksjonen har vi at
Bunnpunktet må da være når
Sammenlikner vi disse svarene med bunnpunktene til grafene får vi at
B må være grafen til , C må være grafen til og A er grafen til .
Svar: tilsvarer B, tilsvarer C, tilsvarer A.
Mer om
Denne oppgaven handler om
Nullpunkt

Punkt der grafen krysser eller tangerer x-aksen. Kan finnes ved regning ved å sette f(x) = 0.
Andregradsuttrykk
Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.
Flere forklaringer og eksempler finner du i lynkurset Funksjonsdrøfting.
For å øve mer, se oppgavesettet om nullpunkter i Treningsleiren.
Oppgave 11 (2 poeng) Nettkode: E-4BLM
Funksjonen er gitt ved
a)
Bestem den momentane vekstfarten til når .
Løsningsforslag a)
Jeg tenker
Den
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Vi finner den momentane vekstfarten til når ved å finne .
Vi starter med å derivere , som er flerleddet uttrykk. Da kan vi derivere ledd for ledd.
Nå kan vi regner ut ved å sette inn :
Svar: Den momentane vekstfarten til når er .
Mer om
Denne oppgavne er om
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere eksempler og forklaringer se artikkelen Å finne tangenten i lynkurset Derivasjon.
For å øve mer, se oppgavesettet om veksthastighet i Treningsleieren.
b)
Bestem den gjennomsnittlige vekstfarten til i intervallet .
Løsningsforslag b)
Jeg tenker
Den
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Vi kan finne den gjennomsnittlige vekstfarten ved å finne stigningstallet til linja som går gjennom punktene og . Stigningstallet til linja kan vi finne ved
.
Men før vi kan finne stigningstallet, må vi regne ut og :
Nå kan vi finne stigningstallet, og med det den gjennomsnittlige vekstfarten, ved å sette inn for :
Svar: Den gjennomsnittelige vekstfarten til i intervallet er .
Mer om
Denne oppgaven handler om
Gjennomsnittlig vekstfart
En funksjon har gjennomsnittlig vekstfart
mellom og . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.
Momentan vekstfart
Den momentane vekstfarten til funksjonen i et punkt , er stigningstallet til tangenten til kurven i punktet.
Flere forklaringer og eksempler finner du i artikkelen Gjennomsnittlig og momentan vekstfart i lynkurset Derivasjon.
For å øve mer, se oppgavesettet veksthastighet i Treningsleieren.
Oppgave 12 (4 poeng) Nettkode: E-4BLQ
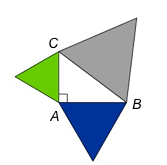
Figuren ovenfor er satt sammen av en rettvinklet trekant og tre likesidede trekanter.
og .
a)
Vis at arealet av den grå trekanten er
Løsningsforslag a)
Jeg tenker
Vi må finne
Høyde
Lengden av et linjestykke som står normalt på ei linje eller en flate.
Arealet av en trekant er gitt ved formelen . Vi kjenner grunnlinjen, , så da gjenstår det å finne høyden.
Vi markerer det siste hjørnet i trekanten som . Høyden i en trekanten finner vi ved å felle en
Normal
En linje som står 90 grader på en annen linje.
Likesidet trekant
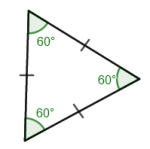
I en likesidet trekant er alle sidene like lange og alle vinklene 60°.
Midtnormal
Midtnormalen til et rett linjestykke er den rette linja som går gjennom linjestykkets midtpunkt, og som står vinkelrett på linjestykket.
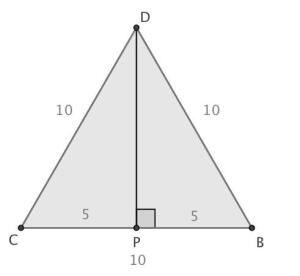
Høyden fra ned på treffer i punktet . Siden er likesidet, er . Høyden halverer , så vi har at .
er rettvinklet, så nå kan vi bruke Pytagoras læresetning tilå finne høyden, :
Nå har vi grunnlinjen og høyden til trekanten, så da kan vi sette inn i formelen for arealet av en trekant.
Mer om
Denne oppgaven handler om
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
Grunnlinje
Grunnlinja er en av sidene i en todimensjonal figur.
Alle sidene kan være grunnlinje. Når vi skal finne høyden i en trekant, må vi vurdere hvilken av sidene som er mest egnet som grunnlinje.
For flere forklaringer og eksempler se artikkelen En trekant i lynkurset Geometri - areal og volum.
For å øve mer, se oppgavesettet om areal i Treningsleieren.
b)
Vis at arealet av den grønne og den blå trekanten til sammen er like stort som arealet av den grå trekanten.
Løsningsforslag b)
Jeg tenker
Hvis vi vet sidelengdene til , kan vi gå fram akkurat som i deloppgave a) for å finne arealene av den grønne og blå trekanten. Siden er en
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Vi begynner med å finne arealet av den blå trekanten, og kan bruke samme framgangsmåte som i deloppgave a) for å finne høyden i trekanten.
Arealet av den blå trekanten blir dermed
Videre finne vi arealet av den grønne trekanten. Da må vi først finne lengden . er en rettvinklet trekant, og vi kan dermed bruke Pytagoras læresetning:
Igjen kan vi bruke samme framgangsmåte som i deloppgave a). Vi finner vi høyden i den grønne trekanten:
Arealet av den grønne trekanten blir da = .
Vi kan nå addere arealen av den grønne og den blå trekanten
,
og vi ser at dette er det samme arealet som den grå.
Mer om
Denne oppgaven handler om
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Pytagoras læresetning

Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Flere forklaringer og eksempler finner du i artikkelen Pytagoras læresetning.
For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleieren.
Oppgave 13 (2 poeng) Nettkode: E-4BLX
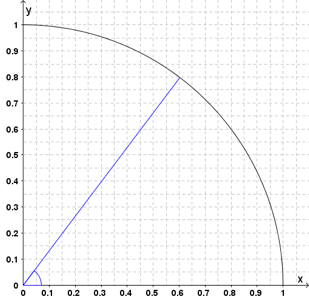
I koordinatsystemet ovenfor er det lagt inn en vinkel på med toppunkt i origo og en kvart sirkel med sentrum i origo og radius .
Bruk koordinatsystemet til å bestemme tilnærmede verdier for , og .
Løsningsforslag
Jeg tenker
Her gjelder det å bruke definisjonene av
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Katet
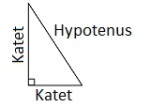
Side i en rettvinklet trekant. Den rette vinkelen dannes av to linjestykker som kalles kateter.
Hypotenus

Den siden som er motstående til den rette vinkelen i en rettvinklet trekant. De andre to sidene kalles kateter.
Vi kaller toppunktet til vinkelen for og punktet der det øvre vinkelbeinet skjærer sirkelen for . Vi feller en normal fra ned på -aksen, og kaller skjæringspunktet . Se figuren under.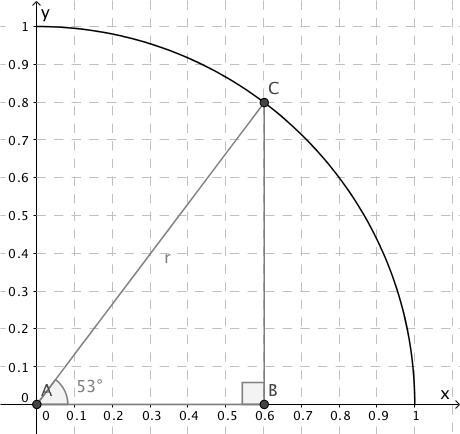
Da har vi en rettvinklet trekant . Sirkelen har radius , og da må . Punktet sine koordinater er omtrent , og da må vi ha at katetene og .
Nå kan vi bruke definisjonene av sinus, cosinus og tangens for å bestemme de tilnærmede verdiene.
Svar:
Mer om
Denne oppgaven handler om
Trigonometri
Læren om forholdet mellom vinkler og sider i en trekant. De trigonometriske funksjonene sinus og cosinus er de viktigste redskapene i denne teorien.
Flere forklaringer og eksempler på hvordan vi finner sinus og cosinus finner du i lynkurset Trigonometri.
For å øve mer, se oppgavesettet om vinkelberegeninger ved hjelp av sinus, cosinus og tangens i Treningsleieren.
Oppgave 14 (4 poeng) Nettkode: E-4BM0
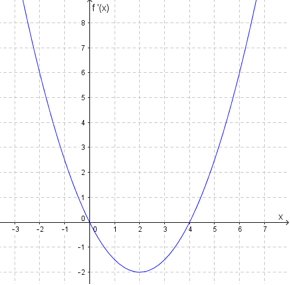
Gitt en funksjon . Ovenfor ser du grafen til den deriverte av funksjonen.
a)
For hvilken verdi av har grafen til et toppunkt?
For hvilken verdi av har grafen til et bunnpunkt?
Løsningsforslag a)
Jeg tenker
Vi ser grafen til den deriverte til , og når den deriverte til en funksjon er positiv stiger funksjonen, og når den deriverte er negativ synker funksjonen. Derfor er vi interessert i å se hvor -verdiene til
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Der grafen til den deriverte er positiv, vil stige og er grafen til deriverte er negativ, vil synke. Utfra grafen til kan vi se at stigningstallet er positivt for og negativt for . Vi kan bruke dette til å
Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
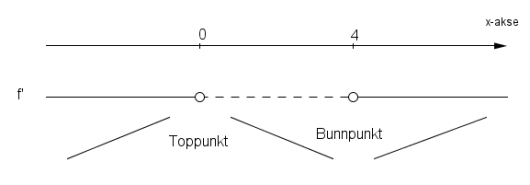
Hvis vi ser på fortegnslinja til kan vi se vi at vil stige fram til , deretter vil den synke mellom og , for så å stige igjen. Toppunktet til må være når , og bunnpunktet til må være når når .
Svar: Toppunkt: , bunnpunkt:
Mer om
Denne oppgaven handler om
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
Fortegnsskjema

Et fortegnsskjema er en grafisk framstilling av hvordan fortegnet til ulike faktorer i et uttrykk endrer seg med x.
Toppunkt

Et toppunkt for en funksjon er et punkt der funksjonsverdien er større enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
For flere eksempler og eksempler se artikkelen Topp- og bunnpunkter i lynkurset Funksjonsdrøfting.
For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleieren.
b)
Punktet ligger på grafen til .
Bestem likningen for tangenten til grafen i dette punktet.
Løsningsforslag b)
Jeg tenker
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Stigningstallet til tangenten er det samme som den deriverte, . Vi leser av grafen til at . Dette betyr at stigningstallet til tangenten til når er .
Siden tangenten er en rett linje med stigningstallet er den på formen . Konstantleddet finner vi ved å bruke at linja går gjennom punktet .
Vi bruker ettpunktsformelen til å finne kontstantleddet :
Svar: Likningen til tangenten til i punktet er gitt ved .
Mer om
Denne oppgaven handler om
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Konstant
En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.
Eksempel: , er en konstant og er en variabel.
Se Variabel
Flere forklaringer og eksempler på hva en tangent er finner du i artikkelen Å finne tangenten og mer om ettpunktsformelen i artikkelen Ettpunktsformelen og likningen for tangentlinjen. Orakelet har også vist hva ettpunktsformelen er.
For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.
DEL 2 Med hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4BNW

Anta at antall registrerte elbiler i Norge år etter 2010 tilnærmet er gitt ved funksjonen der
a)
Bruk graftegner til å tegne grafen til .
Løsningsforslag a)
Jeg tenker
Vi kan bruke
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Vi kan bruke GeoGebra og kommandoen Funksjon[<Funksjon>, <Start>, <Slutt>]. Vi vil tegne grafen for , altså slik at grafen viser for 2010-2018.
Vi skriver inn
i inntastingsfeltet. Vi tilpasser aksene og setter på navn.
Resultatet er vist under.
Svar: 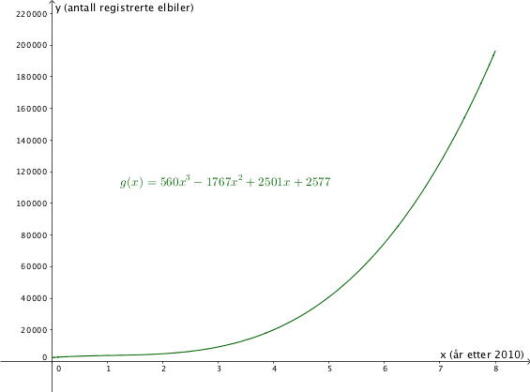
Mer om
Denne oppgaven handler om
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
For flere eksempler og forklaringer om funksjoner se lynkursene Funksjoner (del II) og Funksjonsdrøfting. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om grafisk framstilling i Treningsleiren.
b)
Bestem og .
Hva forteller disse verdiene om antall elbiler?
Løsningsforslag b)
Jeg tenker
Vi kan bruke CAS for å finne og . Alternativt kan vi kan vi bruke grafen og finne tangenten til funksjonen i punktet , da er
Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
I deloppgave a) definerte vi funksjonen , så vi kan bruke samme GeoGebra-fil til å finne og .
Vi finner CAS i "Vis"-menyen i GeoGebra. I første feltet skriver vi inn "g", for å sjekke at den er definert.
For å finne skriver vi inn "g(4)" i neste felt. Da får vi at . Her har vi satt inn i funksjonen vår, så dette forteller oss at år etter , i , vil det være registrerte elbiler i Norge.
Nå skal vi finne , og da skriver vi "g'(4)" inn i neste felt i CAS. Da får vi opp at . Den deriverte forteller oss om stigningen i punktet, så i økte salget av elbiler med biler per år.
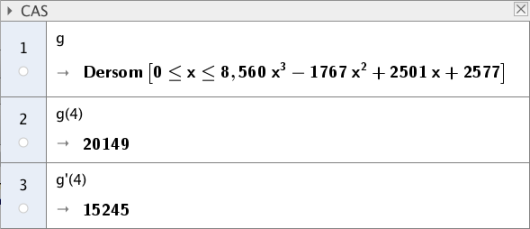
Alternativ løsning
Vi kan finne punktet på grafen når ved å skrive "(4,g(4))" i inntastingsfeltet. Da får vi opp punktet , som forteller oss at .
For å finne tangenten i dette punktet, bruker vi kommandoen Tangent[<Punkt>,<Funksjon>] og skriver inn "Tangent[A, g]". Da får vi opp linjen og leser av at stigningstallet er , altså er
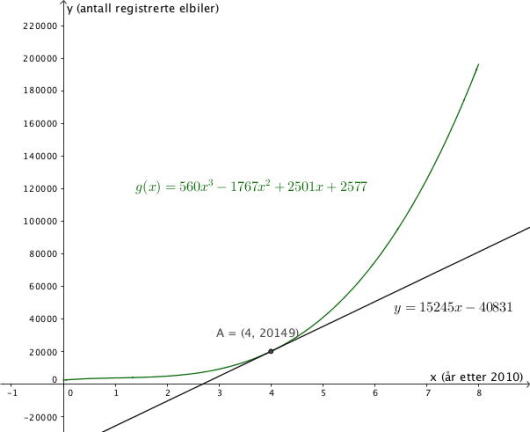
Disse to verdiene forteller oss at i var det registrert elbiler og da økte salget av elbiler med per år.
Svar: og som forteller oss at i var det registrert elbiler og salget økte med per år.
Mer om
Denne oppgaven er om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere eksempler og forklaringer om tangent se artikkelen Å finne tangenten lynkurset Derivasjon.
For å øve mer, se oppgavesettet om veksthastighet i Treningsleiren.
Oppgave 2 (3 poeng) Nettkode: E-4BO0
Tabellen nedenfor viser hvor mange prosent av den norske befolkningen i aldersgruppen 16–74 år som røykte daglig i 2002, 2004, 2006, 2009 og 2012.
| Årstall | 2002 | 2004 | 2006 | 2009 | 2012 |
|
Prosent røykere i aldersgruppen 16-74 år |
29 | 26 | 24 | 20 | 16 |
La være antall år etter 2002. (La svare til år 2002, til år 2003, osv.)
a)
Bruk opplysningene i tabellen til å bestemme en lineær funksjon som viser utviklingen fra 2002 til 2012.
Løsningsforslag a)
Jeg tenker
Vi kan bruke regresjonsfunksjonen i GeoGebra til å finne den
Lineære funksjoner

Lineære funksjoner er funksjoner som er skrevet på formen .
Disse funksjonene er rette linjer der a er stigningstallet og b er punktet grafen krysser y-aksen.
Det første vi må gjøre er å legge inn informasjonen vi har i et regneark i GeoGebra. Det får vi opp ved å velge "Regneark" i "Vis"-menyen.
Vi legger inn antall år etter i første kolonne og prosentandel i andre kolonne.
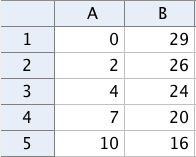
Nå kan vi markere rutene og velge "Regresjonsanalyse" i nedrykksmenyen på knappen med et histogram på. I vinduet som kommer opp velger vi "Analyser".
Da får vi opp
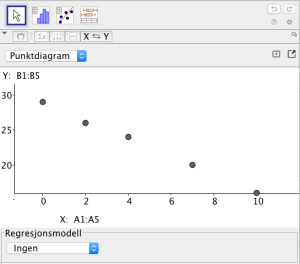
Vi vil ha en lineær modell, så da velger vi "Lineær" under "Regresjonsmodell", og får opp
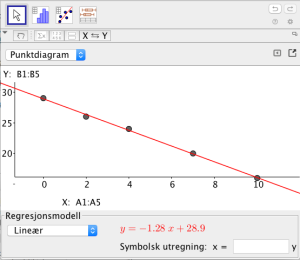
Her kan vi se at er den lineære funksjonen som passer best til informasjonen vi har fått oppgitt.
Alternativ
Etter vi har skrevet inn all informasjonen i regnearket er et annet alternativ og markere alle rutene, høyreklikke og velge "Liste med punkt" under "Lag". Da blir det laget en liste, Liste1, med alle punktene.
Deretter kan vi bruke kommandoen RegLin[<Liste med punkt>], så vi skriver inn "RegLin[Liste1]" og får den lineære funksjonen som passer med punktene.
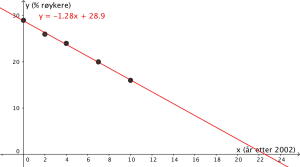
Vi ser at den lineære funksjonen passer med den informasjonen vi har fått.
Svar:
Mer om
Denne oppgaven handler om
Regresjon
Regresjon er å finne en funksjon som passer til et datasett. Altså, en funksjon som går gjennom, eller er nærmest flest mulig punkter i datasettet.
For flere forklaringer og eksempler se artikkelen Regresjon 1.
Lynkurset om GeoGebra er under utarbeidelse og kommer snart.
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.
b)
Vurder om funksjonen kan brukes til å beskrive en videre utvikling fram mot år 2025
Løsningsforslag b)
Jeg tenker
For å vurdere om funksjonen kan beskrive videre utvikling, kan vi lese av grafen fra a)
Fra deloppgave a) har vi grafen til den lineære funksjonen:
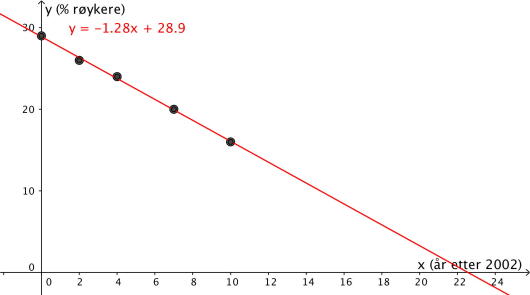
Vi ser at etter , altså i år vil andelen være mindre enn . Dermed kan ikke modellen være gyldig helt til år . Dette betyr likevel ikke at den ikke er gyldig lenger enn til , men den vil etterhvert bli dårligere.
Svar: Funksjonen kan ikke brukes til å beskrive en videre utvikling fram mot år 2025.
Mer om
Denne oppgaven handler om
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Flere eksempler på funksjoner og funksjonsuttrykk finner du i lynkursene Funksjoner (del I) og Funksjoner (del II).
For å øve mer, se oppgavesettet om funksjoner i praktiske situasjoner i Treningsleiren.
Oppgave 3 (4 poeng) Nettkode: E-4BO3
I en 1T-gruppe er det 26 elever. Elevene har valgt fag for neste skoleår.
- 20 elever har valgt faget R1.
- 16 elever har valgt faget Fysikk 1.
- 6 elever har verken valgt R1 eller Fysikk 1.
a)
Systematiser opplysningene i teksten ovenfor i en krysstabell eller i et venndiagram.
Løsningsforslag a)
Jeg tenker
Vi skal lage
Krysstabell
En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
For å sortere dataer og gjøre det enklere å få en oversikt, kan vi enten lage krysstabell eller Venn-diagram. Vi lager en krysstabell her, og viser Venn-diagrammet i alternativ løsning.
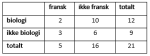
Krysstabellen lager vi ved å bestemme oss for de ulike kategoriene som er rader og kolonner og fyller ut tabellen.
Vi kan begynne med å sette opp en tabell med bare kategoriene:
| Fysikk 1 | Ikke Fysikk 1 | Sum | |
| R1 | |||
| Ikke R1 | |||
| Totalt |
Vi fortsetter med å fylle inn den informasjonen vi har fått oppgitt i oppgaven:
| Fysikk 1 | Ikke Fysikk 1 | Sum | |
| R1 | 20 | ||
| Ikke R1 | 6 | ||
| Totalt | 16 | 26 |
Vi vet at det er elever i klassen, så da kan vi bruke dette til å finne de siste tallene.
Det er elever som har valgt R1, siden det totalt er elever betyr det at det må være elever som ikke har valgt R1, og disse har heller ikke Fysikk 1. Det vil si at vi ikke har noen elever som har valgt Fysikk 1, og ikke har valgt R1.
Vi fyller inn denne informasjonen i tabellen.
| Fysikk 1 | Ikke Fysikk 1 | Sum | |
| R1 | 20 | ||
| Ikke R1 | 0 | 6 | 6 |
| Totalt | 16 | 26 |
Det betyr at alle som har valgt Fysikk 1 også har R1, altså har vi elever som har Fysikk 1 og R1. Siden det er elever som har valgt R1, må vi ha elever som har valgt R1, men ikke Fysikk 1.
Da kan vi fylle inn den siste informasjonen i tabellen.
| Fysikk 1 | Ikke Fysikk 1 | Totalt | |
| R1 | 16 | 4 | 20 |
| Ikke R1 | 0 | 6 | 6 |
| Totalt | 16 | 10 | 26 |
Alternativ
Vi kunne også velge å systematisere opplysningene i et venndiagram. Det vil se ut omtrent slik som dette:
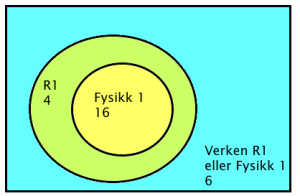
Mer om
Denne oppgaven handler om
Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
For flere forklaringer og eksempler se artikkelen Venn-diagram og mengdelære i lynkurset Sannsynlighet (del II).
b)
Bestem sannsynligheten for at en tilfeldig valgt elev fra gruppen har valgt R1, men ikke Fysikk 1.
Løsningsforslag b)
Jeg tenker
Sidene det er tilfeldig trekning har vi uniform sannsylighet. Vi skal se på forholdet mellom
Gunstig utfall
Et gunstig utfall er den hendelsen som er interessant for oss.
Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.
Se Hendelse
Uniform sannsynlighet er gitt ved
Gunstig utfall er at en valgt elev har valgt R1 men ikke Fysikk 1. Vi leser fra krysstabellen at antall gunstige utfall er 4.
Siden vi velger en tilfeldig elev fra gruppen, er antall mulige utfall hele gruppen, altså 26.
Svar:
Mer om
Denne oppgaven handler om uniform sannsynlighet og
Gunstig utfall
Et gunstig utfall er den hendelsen som er interessant for oss.
Eksempel: Vi skal finne sannsynligheten for å få terningkast 1 eller 6. Av de seks mulige utfallene er 1 og 6 gunstige utfall.
Se Hendelse
For flere forklaringer og eksempler se artikkelen Hvordan finner vi uniform sannsynlighet? i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om uniforme sannsynlighetsmodeller i Treningsleieren.
c)
Det viser seg at eleven som er trukket ut, har valgt Fysikk 1.
Bestem sannsynligheten for at denne eleven også har valgt R1.
Løsningsforslag c)
Jeg tenker
Vi ser på en uniform sannsynlighet der antall gunstige er elever som har valgt både Fysikk 1 og R1, og antall mulige er elever som har valgt Fysikk 1.
Vi ser nøye på krysstabellen i deloppgave a) og finner ut raskt at alle som har valgt Fysikk 1 også har valgt R1. Dette betyr at antall gunstige utfall er lik antall mulige utfall og derfor er sannsynligheten lik .
Vi viser også ved regning. Antall mulige utfall er lik antallet som har valgt Fysikk 1, altså 16. Av disse har alle 16 også alle valgt R1 slik at antall gunstige utfall er 16.
Svar: Sannsynlighet for at en elev som har valgt Fysikk 1 også har valgt R1 er lik .
Mer om
Denne oppgaven handler om
Betinget sannsynlighet
Den betingede sannsynligheten er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.
.
For flere forklaringer og eksempler se artikelene Betinget sannsynlighet og Hvordan finner vi uniform sannsynlighet? i lynkurset Sannsynlighet (del II).
For å øve mer, se oppgavesettet om betinget sannsynlighet og uniforme sannsynlighetsmodeller i Treningsleieren.
Oppgave 4 (3 poeng) Nettkode: E-4BO7
I en rettvinklet trekant er og .
a)
Forklar at det fins to trekanter som oppfyller disse betingelsene.
Løsningsforslag a)
Jeg tenker
Vi har bare fått oppgitt at trekanten er rettvinklet, men ikke hvor den rette vinkelen er. Den kan være Vi bruker
GeoGebra
GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.
Vi kan bruke GeoGebra til å tegne trekantene. Da begynner vi med å tegne inn den informasjonen vi har fått oppgitt:
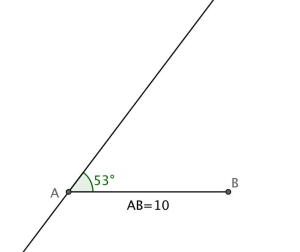
Vi vet at vil ligge på det venstre vinkelbeinet, men vi vet ikke helt hvor, for vi vet ikke hvilken av vinklene som er rettvinklet.
For å se de to alternativene kan vi felle en normal fra ned på det venstre vinkelbeinet, og der de to skjærer vil punktet ligge. Da vil vi ha .
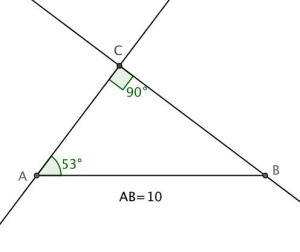
Vi kan også ha , og da vil bli slik: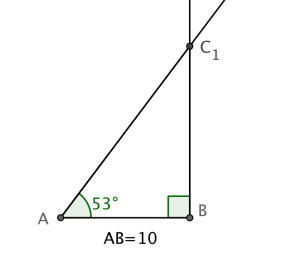
Svar: Siden vi ikke vet hvilken vinkel som er rettvinklet, vil vi få to trekanter.
Mer om
Denne oppgaven handler om
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.
Vinkel
En vinkel er en geometrisk figur satt sammen av to rette linjer med samme startpunkt. Vinkler måles i grader.
For flere forklaringer og eksempler se artikkelen Trekanter.
For å øve mer, se oppgavesettet om trekantberegninger i Treningsleiren.
b)
Bestem for hver av de to trekantene.
Løsningsforslag b)
Jeg tenker
Siden vi har
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.
Vi har to rettvinklede trekanter og da kan vi bruke definisjonene på sinus og tangens til å bestemme i de to trekantene. Vi kan bruke CAS som hjelpemiddel.
I den første trekanten vi fant i deloppgave a)
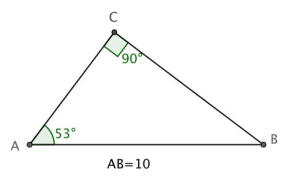
Her kan vi bruke sinus til å finne . Dersom vi ser på har vi at er hypotenusen, og er den motstående kateten. Ved definisjon av sinus får vi
Vi kan bruke CAS til å finne lengden til BC.
Da skriver vi inn
og trykker på ""-tasten.
Da får vi opp

I den andre trekanten, med ,
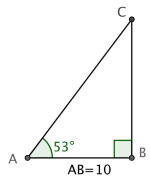
kan vi bruke definisjonen av tangens til å finne .
Nå har vi at , der er motstående katet og er hosliggende.
Vi kan igjen bruke CAS til å finne lengden, og skriver inn
og trykker ""-tasten. Da får vi

Alternativ
Vi kan også bruke resultatet fra oppgave 13 på del 1. Da fant ut at
og .
Vi ser på de to trekantene.
I)
I denne trekanten er motstående katet og hosliggende. Da kan vi bruke definisjonen av tangens
Vi sette inn for og får
II)
I denne trekanten er motstående katet og hypotenusen. Ved å bruke definisjonen av sinus, og sette inn for får vi:
Svar: Når , er . Når , er .
Mer om
Denne oppgaven handler om
Rettvinklet trekant
En rettvinklet trekant er en trekant der en av vinklene er rett, altså 90 grader.
Sinus
Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
Tangens
En trigonometrisk funksjon.
Tangens til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til motstående katet og hosliggende katet.
For flere forklaringer og eksempler se artikkelen Sinus, cosinus og tangens i lynkurset Trigonometri.
For å øve mer, se oppgavesettet om lengdeberegninger ved hjelp av sinus, cosinus og tangens i Treningsleiren.
Oppgave 5 (3 poeng) Nettkode: E-4BOA
En funksjon er gitt ved
Funksjonen har bunnpunkt og et nullpunkt for .
Bruk CAS til å bestemme , og .
Løsningsforslag
Jeg tenker
Vi har tre ukjente, og vi kan bruke opplysningene vi får i oppgaven til å sette opp tre likninger som et likningssystem og bruke CAS til å løse det. Vi husker også at bunnpunktet til en funksjon forteller oss noe om den deriverte til funksjonen i det punktet.
Vi begynner med å se på informasjonen vi blir gitt.
Funksjonen har bunnpunkt , det betyr at .
Videre får vi vite at funksjonen har et nullpunkt for , som vil si at vi må ha .
Vi vet også at i et bunnpunkt vil den deriverte være lik , så . Det gir likningssystemet
Vi kan nå bruke CAS til å løse likningssystemet. Men, før vi skriver inn likningene må vi definere funksjonen . Da skriver vi inn "f(x):=x^3+b*x^2+c*x+d". Videre kan vi skrive inn de likningene vi har: "f(3)=-5", f(4)=0" og "f'(3)=0".
Til slutt bruker vi kommandoen Løs[<Liste med likninger>,<Liste med variabler>].
Siden vi har skrevet inn likningene våre i felt 2,3 og 4, kan vi skrive inn "{$2,$3,$4}" for Liste med likninger, og {b,c,d} for Liste med variabler.
Da får vi

Svar: , og
Mer om
Denne oppgaven handler om
Ligningssett
Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Flere forklaringer og eksempler på hvordan man løser likningssett finner du i lynkurset Lineære likninger med flere ukjente.
For å øve mer, se oppgavesettet om Likningssystemer i Treningsleiren.
Oppgave 6 (3 poeng) Nettkode: E-4BOD
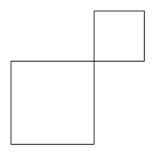
Figuren ovenfor er satt sammen av to kvadrater. I det ene kvadratet har hver side lengde , og i det andre kvadratet har hver side lengde . Omkretsen av hele figuren er 16.
Bestem og slik at det samlede arealet av figuren blir minst mulig.
Løsningsforslag
Jeg tenker
Vi kan bruke det vi vet om
Omkrets

Omkrets er et mål for hvor langt det er rundt en figur, langs sidekantene.
Omkrets er et mål for lengde. Derfor måles omkrets i meter eller i en lengdeenhet avledet av meter.
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Omkretsen til kan uttrykkes , og denne vet vi er , altså må vi ha . Dette kan vi bruke til å finne ut uttrykk for ;
.
Arealet til hele figuren er summen av arealene til de to kvadratene, så
Nå setter vi inn uttrykket for , slik at vi har en funksjon for arealet gitt ved kun :
Siden er en andregradsfunksjon med positiv andregradskoeffisient, så vet vi at har et bunnpunkt. For å finne bunnpunktet til deriverer vi funksjonen og setter den deriverte lik 0:
Vi setter inn for i uttrykket for :
Vi har det minste arealet når og . Det minste arealet har vi når de to kvadratene er like store.
Alternativ
Vi kan også bruke GeoGebra til å tegne grafen til arealfunksjonen. Over fant vi ut at vi kan skrive den som
Vi skriver den inn i GeoGebra og bruker kommandoen Ekstremalpunkt ved å skrive inn "Ekstremalpunkt[A]". Da får vi opp punktet , som forteller oss at arealet er minst når , og da vil vi ha et areal på .
Vi setter inn i uttrykket for og får
Arealet er minst når .
Svar: Arealet er minst når og .
Mer om
Denne oppgaven handler om
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
Bunnpunkt

Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt .
Derivasjon
En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.
For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkt og lynkurset Derivasjon.
For å øve mer, se oppgavesettet om derivasjon i Treningsleiren.
Oppgave 7 (4 poeng) Nettkode: E-4BOG
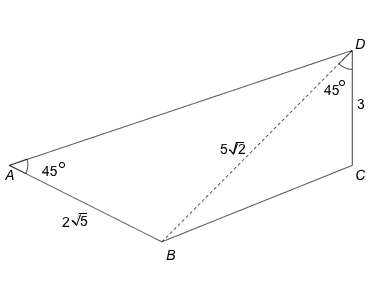
Gitt firkanten ovenfor. , og .
Bruk CAS til å bestemme arealet av firkanten eksakt.
Løsningsforslag
Jeg tenker
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2.
Arealsetningen
For en trekant er arealet gitt ved .
Vi kan finne arealet av hver av trekantene
Arealsetningen sier at for en trekant er arealet gitt ved
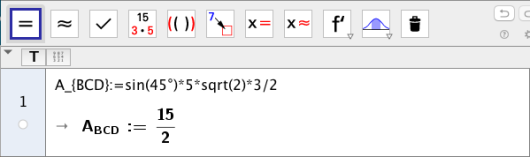
I trekant kjenner vi og sidene og kan sette rett inni arealsetningen:
Vi bruker CAS til å regne ut arealet eksakt:
Videre ser vi på trekanten . Her kjenner vi og , men trenger å vite lengden til for å bruke arealsetningen. For å finne denne siste sidelengden, bruker vi
Cosinussetningen
La være en trekant. Anta at vi kjenner sidene , og mellom dem. Da er
NÅ kan vi bruke CAS til å regne ut :

Vi vil finne lengden på AD, så vi kan se bort fra den negative verdien og får da at .
Nå kan vi bruke arealsetningen
til å finne arealet til trekant og deretter kan vi summere sammen de to arealene:

Summen av arealet til de to trekantene er .
Svar: Arealet er .
Mer om
Denne oppgaven handler om
Arealsetningen
For en trekant er arealet gitt ved .
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
For flere forklarigner og eksempler se artiklene Arealsetningen og Cosinussetningen i lynkurset Trigonometri.
For å øve mer, se oppgavesettet om cosinussetningen i Treningsleiren.




