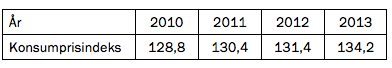Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1011 2014 Høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Skatteoppgjør: (http://www.tu.no/, 4.07.2016)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4AMA
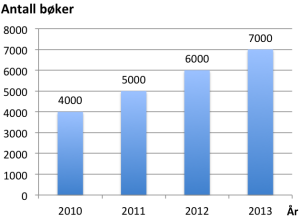
Diagrammet ovenfor viser hvor mange bøker en forfatter har solgt hvert år de fire siste årene.
Når var den prosentvise økningen i salget fra et år til det neste størst?
Oppgave 2 (1 poeng) Nettkode: E-4AMC
Ifølge en oppskrift trenger du 500 g kjøttdeig for å lage middag til fire personer.
Hvor mye kjøttdeig trenger du for å lage middag til ni personer?
Oppgave 3 (2 poeng) Nettkode: E-4AME
I basisåret kostet en vare 600 kroner. I 2013 kostet varen 720 kroner. Vi antar at prisen for varen har fulgt indeksen.
Bestem indeksen for varen i 2013.
Oppgave 4 (2 poeng) Nettkode: E-4AMG
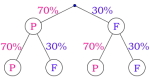
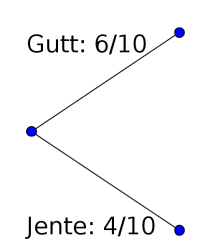
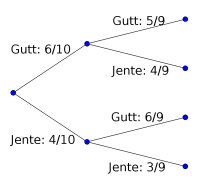
I en klasse er det seks gutter og fire jenter. To elever velges tilfeldig til å være med i en spørreundersøkelse.
Tegn et valgtre, og bruk dette til å bestemme sannsynligheten for at én jente og én gutt velges ut.
Oppgave 5 (2 poeng) Nettkode: E-4AMJ
Trond påstår at antall kiwi du kjøper i denne butikken, og beløpet du betaler for kiwiene, er proporsjonale størrelser. Therese mener det ikke er grunnlag for å påstå dette.
Hvordan kan Trond og Therese argumentere?
Oppgave 6 (3 poeng) Nettkode: E-4AML
I 2006 kostet en vare 600 kroner. I 2014 koster varen 1 000 kroner.
a)
I løpet av disse åtte årene har prisen økt lineært. Forklar hva det vil si.
b)
Vi antar at prisen fortsetter å øke lineært.
Bestem en funksjon som viser prisen kroner for varen år etter 2006.
c)
Hvor mye vil varen koste i 2018 ifølge funksjonen i oppgave b)?
Oppgave 7 (4 poeng) Nettkode: E-4AMQ
Julie har fått følgende oppgave:
«En formiddag i barnehagen var det fem ganger så mange barn ute som inne. Etter lunsj kom tre barn til ut. Da ble det åtte ganger så mange barn ute som inne.
Hvor mange barn var det i barnehagen denne dagen?»
Hun arbeider med teksten, og setter først opp en tabell:
| Inne | Ute |
Så setter hun opp denne likningen:
a)
Forklar hvordan Julie kommer fram til uttrykkene som er satt inn i tabellen, og hvordan hun kommer fram til likningen.
b)
Løs likningen.
Hvor mange barn var det i barnehagen denne dagen?
Oppgave 8 (4 poeng) Nettkode: E-4AMU
a)
Hva kjennetegner et annuitetslån?
Hva kjennetegner et serielån?
b)
Siv tar opp et annuitetslån på 2 000 000 kroner. Solveig tar opp et serielån på
2 000 000 kroner. Begge får samme rentesats, og de skal betale ned lånene over like lang tid.
Hvorfor må Siv totalt betale mer tilbake til banken enn Solveig?
c)
Hvorfor kan det for noen være gunstig å velge et annuitetslån framfor et serielån?
Oppgave 9 (4 poeng) Nettkode: E-4AMZ
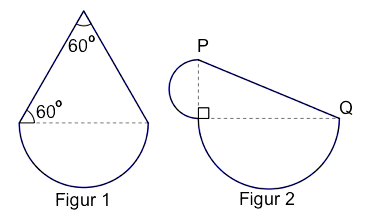
Figur 1 ovenfor er sammensatt av en trekant og en halvsirkel. Halvsirkelen har radius 5,5.
Figur 2 er sammensatt av en trekant og to halvsirkler. Den minste halvsirkelen har radius 2,5 og den største har radius 6,0.
a)
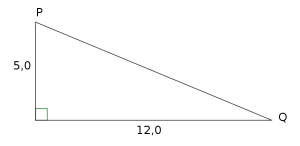
Vis at linjestykket PQ har lengde 13.
b)
Gjør beregninger, og avgjør hvilken figur som har størst omkrets.
DEL 2 Med hjelpemidler
Oppgave 1 (4 poeng) Nettkode: E-4AN3
Da skatteetaten la ut det foreløpige skatteoppgjøret på nett 19. mars i år, var dette en av overskriftene på nettsidene til Teknisk Ukeblad:
selvangivelsen 2013
45 pålogginger hvert sekund for å sjekke skatten
Anta at pågangen var like stor hele denne dagen.
a)
Hvor mange hadde da logget seg på i løpet av én time?
b)
Omtrent 900 000 skattytere fikk skatteoppgjøret sitt elektronisk denne dagen.
Hvor lang tid ville det gått før alle hadde logget seg på?
c)
Nedenfor ser du et annet sitat fra nettet i forbindelse med skatteoppgjøret.
Onsdag 19. mars kan nær 900 000 skattytere sjekke selvangivelse...
«I denne omgang er det bare elektroniske brukere (e-brukere) som får tilgang til selvangivelsen. Resten, det vil si rundt 3,7 millioner innbyggere, må vente til 1. april før de får skattedommen.»
Hvor mange prosent av skattyterne i Norge er elektroniske brukere?
Oppgave 2 (4 poeng) Nettkode: E-4AN9
Funksjonen er gitt ved
a)
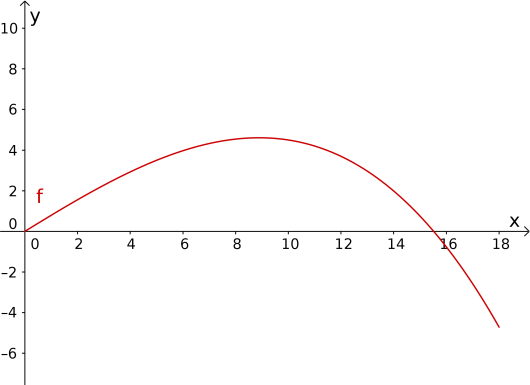
Tegn grafen til .
b)
Bestem nullpunktene til .
Bestem toppunktet på grafen til .
c)
En sommernatt begynte det å snø i en fjellbygd. Når viser funksjonen
snødybden cm i bygda timer etter midnatt.
Hva forteller svarene du fant i oppgave b) om snødybden i fjellbygda?
Oppgave 3 (5 poeng) Nettkode: E-4ANU
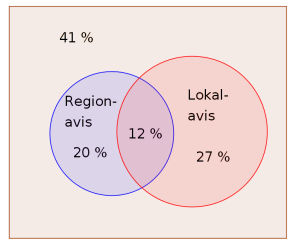
I en by abonnerer av husstandene på lokalavisen, mens av husstandene abonnerer på regionavisen. av husstandene abonnerer ikke på noen av de to avisene.
a)
Systematiser opplysningene ovenfor i et venndiagram eller en
Krysstabell
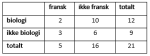
En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.
b)
En husstand i byen abonnerer på regionavisen.
Bestem sannsynligheten for at denne husstanden også abonnerer på lokalavisen.
c)
Tre husstander i byen velges ut tilfeldig.
Bestem sannsynligheten for at akkurat én av husstandene abonnerer på lokalavisen.
Oppgave 4 (6 poeng) Nettkode: E-4ANZ
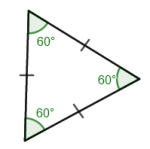
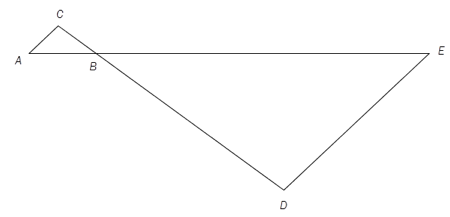
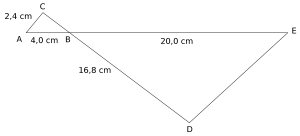
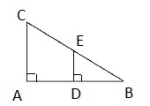
og er formlike.
cm
cm
cm
cm
a)
Bestem lengden av ved regning.
b)
Bestem lengden av ved regning.
c)
Arealet av er .
Bestem arealet av ved regning.
Oppgave 5 (4 poeng) Nettkode: E-4AO4
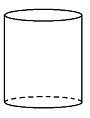
Stanley har laget en sopp som skal brukes i en juleutstilling. Soppen er en sylinder med en halvkule på toppen.
Sylinderen har radius 2,0 dm, og halvkulen har radius 4,0 dm. Høyden i sylinderen er lik radien i halvkulen.
a)
Bestem volumet av soppen.
b)
Stanley skal male soppen. 1 L maling er nok til 6 m2.
Hvor mye maling trenger han?
Oppgave 6 (4 poeng) Nettkode: E-4AO9
I 2011 flyttet Per inn i ny leilighet. Husleien var da 8000 kroner per måned. I leiekontrakten til Per står det blant annet:
a)
Vis at månedsleien fra og med januar 2012 var 8100 kroner.
b)
Hvor mye betalte Per til sammen i husleie fra og med januar 2012 til og med desember 2013?
Oppgave 7 (7 poeng) Nettkode: E-4AOD
Arne opprettet en høyrentekonto i banken 1. januar 2014 og satte inn 75 000 kroner. Renten er 1,75 % per år.
a)
Hvor mye vil han ha i banken 1. januar 2017?
b)
Eirik opprettet en BSU-konto (boligsparing for ungdom) i banken 1. januar 2014 og satte inn 25 000 kroner. Renten er 4,5 % per år. Eirik vil sette inn 25 000 kroner på kontoen 1. januar 2015 og 1. januar 2016.
Hvor mye vil han ha i banken 1. januar 2017?
c)
Eirik får et skattefradrag på 20 % av beløpet han setter inn på kontoen hvert år.
Vis at dette betyr at han til sammen betaler 15 000 kroner mindre i skatt i løpet av disse tre årene enn han ellers ville ha gjort.
d)
Vis at når vi ser på renter og skattefradrag, «tjener» Eirik omtrent 448 % mer enn Arne ved å velge BSU framfor høyrentekonto.
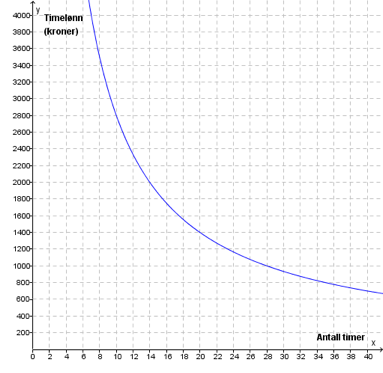
Oppgave 8 (2 poeng) Nettkode: E-4AOJ
Maler Jensen tilbyr en kunde en fast pris for å male et hus. Grafen ovenfor viser sammenhengen mellom antall timer Jensen bruker på jobben, og timelønnen han vil få.
Bestem Jensens timelønn dersom han bruker 64 timer på jobben.