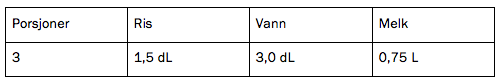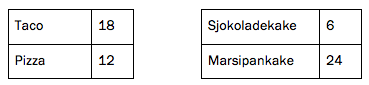Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1011 2013 Vår
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Melk: (http://www.tine.no, 4.07.2016)
- Poteter: (http://www.freeimages.com/, 4.07.2016)
- Ost: (www.tine.no, 4.07.2016)
- Skinke: (http://www.matstart.no/, 4.07.2016)
- Hjort: (http://www.freeimages.com/, 4.07.2016)
- Tørr sand: (http://forskning.no/, 4.07.2016)
Tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (2 poeng) Nettkode: E-4AB4
Hilde skal kjøpe
2 L melk
2,5 kg poteter
0,5 kg ost
200 g kokt skinke
Gjør et overslag og finn ut omtrent hvor mye hun må betale.
Oppgave 2 (2 poeng) Nettkode: E-4AB1
En vare koster nå 210 kroner. Prisen er da satt ned med 30 %.
Hva kostet varen før prisen ble satt ned?
Oppgave 3 (2 poeng) Nettkode: E-4AB6
En vare kostet 150 kroner i basisåret. I dag er indeksen for varen 110.
Hvor mye koster varen i dag dersom vi antar at prisutviklingen har fulgt utviklingen i indeksen?
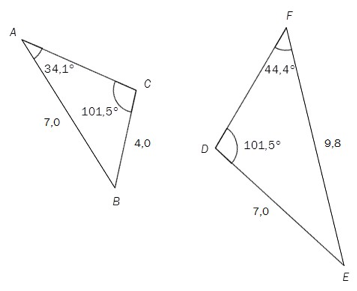
Oppgave 4 (3 poeng) Nettkode: E-4AB9
a)
Vis at de to trekantene ovenfor er formlike.
b)
Bestem lengden av sidene AC og DF .
Oppgave 5 (3 poeng) Nettkode: E-4AE4
På en pakke grøtris står følgende opplysninger:
a)
Hvor mye ris, vann og melk trenger du for å lage 10 porsjoner med grøt?
b)
Du har nok vann og ris, men du har bare 5 L melk.
Hvor mange porsjoner grøt kan du lage?
Oppgave 6 (4 poeng) Nettkode: E-4AGD
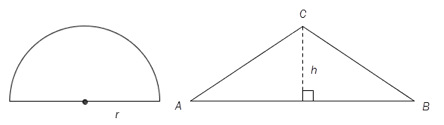
Et område har form som en halvsirkel med radius m. Et annet område har form
som en likebeint , der m og høyden m. Se figurene ovenfor.
Gjør beregninger og svar på spørsmålene under.
a)
Hvilket av de to områdene har størst areal?
b)
Hvilket av de to områdene har størst omkrets?
Oppgave 7 (5 poeng) Nettkode: E-4AHG
I en tank er det 60 L vann. Hver dag tapper vi 5,0 L vann fra tanken.
a)
Hvor mye vann er det igjen i tanken etter åtte dager?
Hvor mange dager går det før tanken er tom?
b)
Bestem funksjonsuttrykket til en funksjon som viser hvor mange liter vann det er igjen i tanken etter dager.
c)
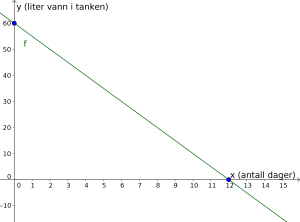
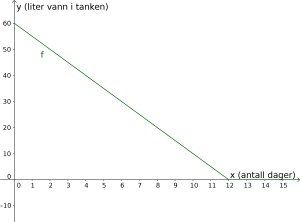
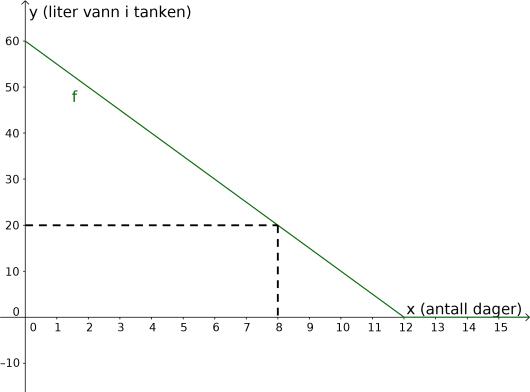
Tegn grafen til .
Vis hvordan du kan bruke grafen til å finne svar på spørsmålene i oppgave 7 a).
Oppgave 8 (3 poeng) Nettkode: E-4AIT
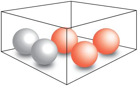
I en eske er det tre røde og to blå kuler. Sondre trekker tilfeldig to av kulene.
a)
Bestem sannsynligheten for at han trekker to røde kuler.
b)
Bestem sannsynligheten for at de to kulene han trekker, har samme farge.
DEL 2 Med hjelpemidler
Oppgave 1 (8 poeng) Nettkode: E-4AIX
Ole arbeider på et mekanisk verksted. Han har en timelønn på 195 kroner innenfor vanlig arbeidstid. Nedenfor ser du hvor mange timer han arbeidet en måned.
a)
Bestem bruttolønna til Ole denne måneden.
b)
Ole betaler 2 % av bruttolønna til en pensjonskasse.
Hvor mye betalte Ole til pensjonskassen denne måneden?
c)
Ole betaler 36 % skatt.
Hvor mye fikk Ole utbetalt etter at skatten var trukket fra, denne måneden?
d)
En periode arbeidet Ole med et prosjekt på kveldstid. For timene han brukte på dette prosjektet, fikk han overtid med 50 % tillegg. Han fikk utbetalt 5045 kroner for arbeidet.
Hvor mange timer arbeidet han med prosjektet?
Oppgave 2 (5 poeng) Nettkode: E-4AJ3
I en klasse er det 30 elever. Klassen skal arrangere fest. Elevene må bestemme seg for om de vil ha taco eller pizza til middag, og om de vil ha sjokoladekake eller marsipankake til dessert.
Hver elev legger en lapp med hvilken middag de ønsker, i én krukke og en lapp med hvilken kake de ønsker, i en annen krukke.
Nedenfor ser du hvordan ønskene fordeler seg.
For å avgjøre hva menyen skal være, trekker læreren tilfeldig en lapp fra hver krukke.
a)
Bestem sannsynligheten for at det blir taco til middag.
b)
Bestem sannsynligheten for at det blir taco til middag og marsipankake til dessert.
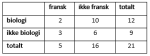
c)
4 elever vil ha pizza og sjokoladekake.
Vi trekker tilfeldig ut en elev.
Bestem sannsynligheten for at eleven vil ha taco og marsipankake.
Oppgave 3 (6 poeng) Nettkode: E-4AK4
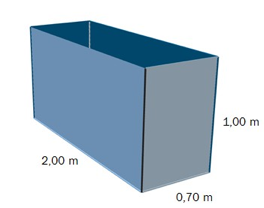
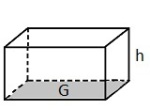
Familien Hansen har hytte på fjellet. I kjelleren har de en beholder der de samler opp regnvann. Beholderen har form som et rett firkantet prisme. Se skissen ovenfor.
a)
Hvor mange liter rommer beholderen?
b)
Når det regner, vil alt vannet som treffer hyttetaket, bli ledet ned i beholderen. Hyttetaket er tilnærmet horisontalt og har et areal på 70 m2. En dag da familien reiser fra hytta, er beholderen tom. I løpet av den neste uken regner det 12 mm.
Hvor høyt i beholderen står vannet når familien kommer tilbake etter denne uken?
c)
En annen dag familien reiser fra hytta, står vannet 10 cm høyt i beholderen. Når de kommer tilbake, står vannet 85 cm høyt.
Hvor mange millimeter har det regnet den tiden de var borte?
Oppgave 4 (8 poeng) Nettkode: E-4AK9
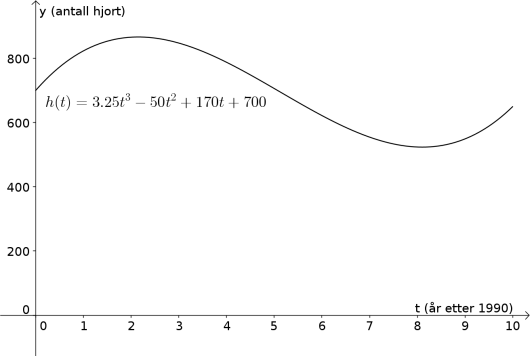
Funksjonen gitt ved
var en god modell for hjortebestanden i en kommune i perioden 1990–2000.
Ifølge modellen var det hjort i kommunen t år etter 1. januar 1990.
a)
Tegn grafen til for
b)
Når var hjortebestanden størst, og hvor mange hjort var det i kommunen da?
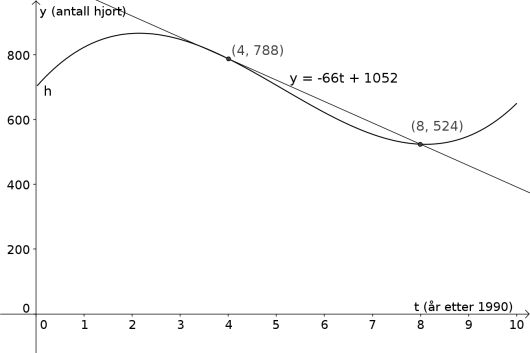
c)
Løs likningen grafisk, og forklar hva løsningen forteller om hjortebestanden.
d)
Hvor stor var den gjennomsnittlige endringen i antall hjort per år i perioden
1. januar 1994–1. januar 1998?
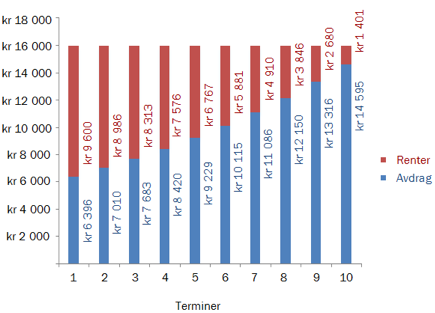
Oppgave 5 (5 poeng) Nettkode: E-4ALE
Ovenfor ser du nedbetalingsplanen for et lån som betales ned i løpet av 10 terminer.Hver termin er 1 år. Renten i prosent er den samme i hele nedbetalingsperioden.
a)
Forklar hvilken type lån dette er.
b)
Hvor stort er det totale lånebeløpet?
c)
Hvor mange prosent er renten på?
Oppgave 6 (4 poeng) Nettkode: E-4ALK
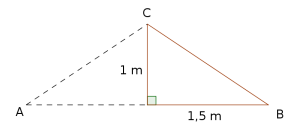
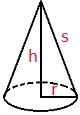
En haug med tørr sand har form tilnærmet lik en kjegle. Radius i kjeglen er 1,5 ganger så stor som høyden i kjeglen.
a)
Bestem volumet av haugen med tørr sand dersom radius i kjeglen er 1,35 m.
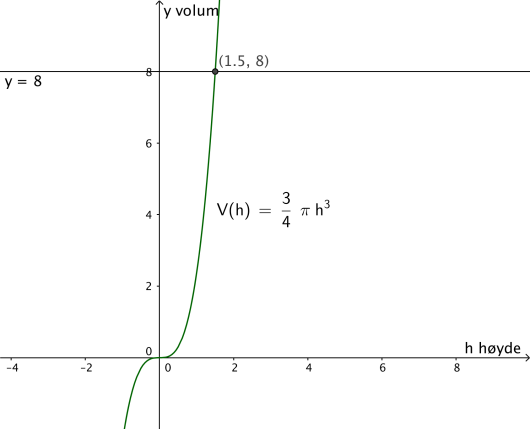
b)
Bestem hvor høy kjeglen er dersom haugen med sand har et volum på 8,0 m3.