Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.
Våre samarbeidspartnere:

MAT1011 2013 høst
Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.
Hjelpemidler:
Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
Framgangsmåte:
Du skal svare på alle oppgavene.
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.
Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du
- viser regneferdigheter og matematisk forståelse
- gjennomfører logiske resonnementer
- ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
- kan bruke hensiktsmessige hjelpemidler
- vurderer om svar er rimelige
- forklarer framgangsmåter og begrunner svar
- skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
Andre opplysninger:
Kilder for bilder, tegninger osv.
- Fisk: http://www.imr.no/nyhetsarkiv/2009/august/flere_grunner_til_gode_fiskebestander_i_barentshavet/nb-no (13.01.2013)
- Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet
DEL 1 Uten hjelpemidler
Oppgave 1 (1 poeng) Nettkode: E-49RZ
Per har lest 150 sider i en bok. Dette er 30 % av sidene i boka.
Hvor mange sider er det i boka?
Oppgave 2 (1 poeng) Nettkode: E-49S4
På et kart er avstanden fra et punkt A til et punkt B 2,0 cm. I virkeligheten er avstanden i luftlinje mellom disse to punktene 10 km.
Bestem målestokken til kartet.
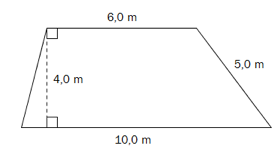
Oppgave 3 (2 poeng) Nettkode: E-49TC
Et område har form som vist på figuren ovenfor.
Bestem arealet av området.
Oppgave 4 (2 poeng) Nettkode: E-49TQ
Et år hadde Ole en reallønn på 500 000 kroner. Konsumprisindeksen dette året var 130.
Bestem den nominelle lønna til Ole dette året.
Oppgave 5 (2 poeng) Nettkode: E-49TW
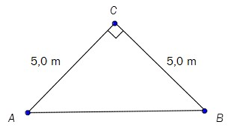
Et område har form som vist på figuren ovenfor.
Avgjør ved regning om avstanden fra A til B er lengre enn 7,0 m.
Oppgave 6 (2 poeng) Nettkode: E-49TY
Skriv av, gjør beregninger, og sett inn tallene som mangler i hver av linjene:
_____________ L
og _____________ min
Oppgave 7 (3 poeng) Nettkode: E-49U0
Sammenhengen mellom maksimal puls M (antall slag/min) og alder A (antall år) er gitt ved formelen
a)
Hva er maksimal puls til en person som er 20 år, ifølge formelen ovenfor?
b)
Svein har en maksimal puls på 179 slag/min.
Hvor gammel er Svein ifølge formelen ovenfor?
Oppgave 8 (4 poeng) Nettkode: E-49U6
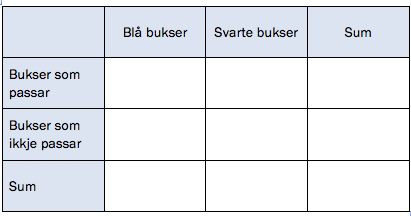
Siv har fire blå og seks svarte bukser i skapet. Én av de blå og tre av de svarte buksene passer ikke lenger.
a)
Tegn av tabellen nedenfor, og fyll inn tall i de hvite rutene.
b)
Siv tar tilfeldig én bukse fra skapet.
Bestem sannsynligheten for at buksen passer.
c)
Siv har tatt en bukse som passer.
Bestem sannsynligheten for at denne buksen er blå.
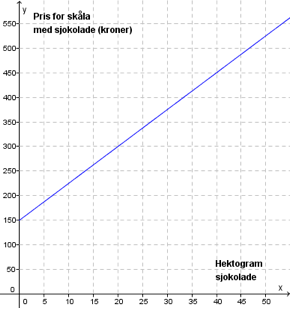
Oppgave 9 (3 poeng) Nettkode: E-49UD
Terje kjøper en skål og fyller den med sjokolade. Den rette linjen i koordinatsystemet ovenfor viser sammenhengen mellom antall hektogram sjokolade Terje kjøper, og hvor mye han må betale for skålen med sjokolade.
a)
Hvor mye koster selve skålen?
Hvor mye koster 1 hg sjokolade?
b)
Bestem likningen for den rette linjen.
Oppgave 10 (2 poeng) Nettkode: E-49UK
Ovenfor ser du hvor mye tre ulike pakker kjøttdeig koster i en butikk.
Er vekt og pris proporsjonale størrelser her?
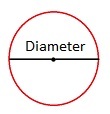
Oppgave 11 (2 poeng) Nettkode: E-49UR
Maria lurer på hvor stor diameter en ball har. Hun måler langs ballens overflate og finner at det er ca. 100 cm fra A til B. Se bildet ovenfor.
Gjør overslag, og bestem omtrent hvor stor diameter ballen har.
DEL 2 Med hjelpemidler
Oppgave 1 (6 poeng) Nettkode: E-49UV
Tabellen ovenfor viser konsumprisindeksen (KPI) hvert år fra 2008 til 2012.
a)
Hvor mange prosent har konsumprisindeksen økt med i denne perioden?
b)
I 2010 kjøpte familien Johnsen matvarer for 8000 kroner per måned. Vi antar at prisen på disse matvarene har fulgt utviklingen i konsumprisindeksen.
Hvor mye betalte familien per måned for tilsvarende matvarer i 2012?
c)
I 2008 var inntekten til familien Johnsen 45 000 kroner per måned. I 2012 var inntekten økt til 49 000 kroner per måned.
Gjør beregninger og avgjør om familien hadde større kjøpekraft (bedre råd) i 2012 enn i 2008.
Oppgave 2 (4 poeng) Nettkode: E-49V3
En undersøkelse har vist at 20 % av alle syklistene i en by sykler uten lys i mørket. Vi velger tilfeldig to syklister fra denne byen.
a)
Bestem sannsynligheten for at begge sykler uten lys i mørket.
b)
Bestem sannsynligheten for at nøyaktig én av dem sykler uten lys i mørket.
Oppgave 3 (4 poeng) Nettkode: E-49V7
Øystein har kjøpt bil. Bilen kostet 250 000 kroner. Vi regner med at verdien har sunket, og at den vil fortsette å synke, med 15 % per år.
a)
Hvor mye vil bilen være verd om fem år?
b)
Hvor mye var bilen verd for fem år siden?
Oppgave 4 (5 poeng) Nettkode: E-49VG
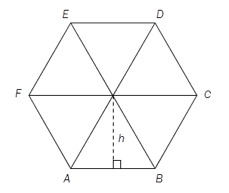
En regulær sekskant er satt sammen av seks likesidede trekanter. Sidene i trekantene er 3,0 cm. Se figuren ovenfor.
a)
Bestem .
b)
Bestem høyden i trekantene ved regning.
c)
Bestem arealet av sekskanten ved regning.
Oppgave 5 (8 poeng) Nettkode: E-49W8
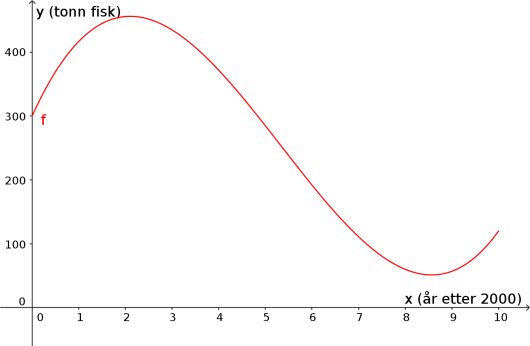
Funksjonen gitt ved
viser hvor mange tonn fisk det var i en fiskebestand år etter år 2000.
a)
Tegn grafen til for .
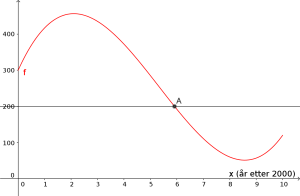
b)
Når var fiskebestanden minst?
Hvor mange tonn fisk var det i fiskebestanden da?
c)
Bestem skjæringspunktet mellom grafen til f og linjen med likning .
Hva forteller koordinatene til dette punktet om fiskebestanden?
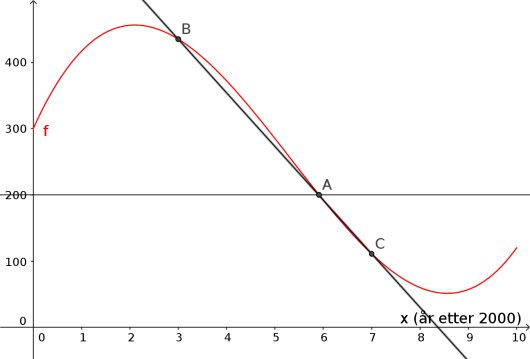
d)
Hvor stor var den gjennomsnittlige endringen i fiskebestanden per år i perioden 1. januar 2003 – 1. januar 2007?
Oppgave 6 (4 poeng) Nettkode: E-49WK
Jonny er rørlegger. Han har en timelønn på 215 kroner.
Jonny betaler 2 % av bruttolønna til en pensjonskasse. I tillegg betaler han hver måned 250 kroner i fagforeningskontingent.
En måned arbeidet Jonny 150 timer.
a)
Hvor mye betalte Jonny til pensjonskassen denne måneden?
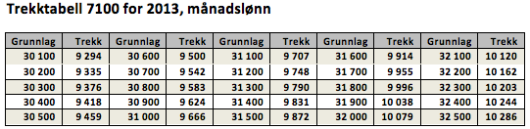
b)
Jonny har tabelltrekk. Se nedenfor.
Hvor mye betalte han i skatt denne måneden?
Oppgave 7 (5 poeng) Nettkode: E-4EI6
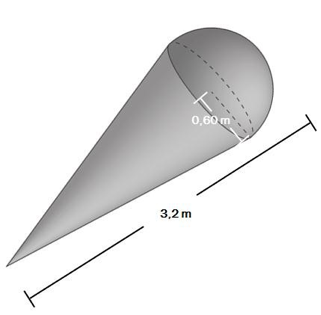
Tore har laget en stor modell av en kuleis. Modellen har tilnærmet form som en kjegle med en halvkule i enden. Toppen av kjeglen har radius , og modellen er lang. Se skissen ovenfor.
a)
Regn ut volumet av modellen.
b)
Modellen skal lakkeres. En boks lakk er nok til 2,2 m2.
Hvor mange bokser vil gå med for å lakkere modellen?