Jean Baptiste Joseph Fourier

Jean Baptiste Joseph Fourier
Fourier ble regnet som Newton nummer 2, og utviklet teknikker som brukes den dag i dag både i ren og anvendt matematikk. Du har kanskje hørt om Fourier-rekker og -transformasjoner?
Joseph Fourier var født i Auxerre i Frankrike i 1768 som tolvte barn i en skredderfamilie. I tiårsalderen ble han foreldreløs, men hans begavelse hadde allerede vist seg, og han fikk gratisplass ved en skole drevet av Benediktinerordenen. Han ville bli artillerist, men fikk vite at denne karrieren var forbeholdt adelig det fikk ikke hjelpe om han var en Newton nummer to. Denne opplevelsen styrket ikke Fouriers tiltro til den eksisterende samfunnsorden, og han sluttet han seg helhjertet til den franske revolusjonen i 1789. Etter hvert som revolusjonen utviklet seg til en innbyrdes kamp mellom ulike fraksjoner, ble Fourier vekselvis arrestert og løslatt. Flere ganger sto han i fare for å bli henrettet, og en gang skal han bare ha blitt reddet av Robespierres fall. Istedenfor å miste hodet fikk Fourier stilling ved den nye eliteskolen Ecole Normal, der han fikk flere av tidens ledende matematikere som kolleger.
I 1798 deltok Fourier i Napoleons felttog til Egypt. Hans hovedinnsats var å organisere arbeidet med en beskrivelse av Egypts geografi og historie, og han skrev selv en innledning som ennå idag regnes som et gjennombrudd i egyptologien. Senere ble han ivrig støttespiller i Jean François Champollions (1790-1832) arbeid med å tyde hieroglyfene. I Egypt hadde Fourier flere administrative poster, og ved tilbakekomsten til Frankrike gjorde Napoleon ham til prefekt i området rundt Grenoble. Fourier var utvilsomt en dyktig administrator, og da Napoleon falt i 1814 og makten gikk tilbake til Bourbonfamilien, lot kong Ludvig XVIII ham beholde posten.
I 1815 vendte Napoleon tilbake fra det lille keiserdømmet han hadde fått beholde på Elba, og marsjerte mot Paris med en styrke på 1100 mann. Uten at et skudd ble løsnet, deserterte kongens soldater og gikk over til keiseren, og Napoleons styrke vokste gradvis mens han nærmet seg Paris. Grenoble var den første store byen han kom til på sin ferd. Fourier gjorde sitt beste for å organisere væpnet motstanden, men alt var nytteløst, og sammen med sine medarbeidere forlot han byen i det øyeblikket Napoleon red inn gjennom hovedporten. Keiserens triumferd må ha gjort inntrykk på Fourier fem dager senere byttet han side, ble adlet og utnevnt til prefekt i Rhône-området. Men Napoleons nye styre skulle bare vare i hundre dager, og da Ludvig XVIII vendte tilbake etter slaget ved Waterloo, var det slutt på Fouriers administrative karriere. Han ble nektet den pensjonen han normalt ville ha fått, og det så mørkt ut inntil en av hans tidligere elever skaffet ham stilling som direktør ved det statistiske kontoret for Seinedalen. Også på dette området gjorde Fourier et praktisk reformarbeid som fortsatt huskes. I 1816 ble han valgt inn i vitenskapsakademiet i Paris, men kongen nektet å godkjenne utnevnelsen. Året etter gikk imidlertid utnevnelse igjennom, og i 1822 ble Fourier valgt til akademiets permanente sekretær.
Hans viktigste matematiske bidrag ble formulert allerede i 1807 da han innleverte en avhandling om varmeledning til det franske vitenskapsakademiet. Fouriers utgangspunkt var spørsmålet om hvordan varme brer seg i faste stoffer. Varmer du opp en metallstang i den ene enden, vil varmen etterhvert bre seg til hele stangen, men hvor fort vil dette skje, og hvor store temperaturforskjeller vil det være langs stangen? Fouriers mål var å besvare alle slike spørsmål ved å finne et uttrykk u(x, t) for temperaturen i punktet x ved tiden t.
Fourier oppdaget at han kunne løse problemet ved å skrive generelle funksjoner som uendelige summer av sinus-er og cosinus-er. Men Fourier greide også det Bernoulli og Euler før ham ikke hadde greid, nemlig å finne de tallene som skal til for at summen
skal bli lik en gitt funksjon .
Dessverre klarte ikke Fourier å bevise at metoden hans fungerte, og ledende franske matematikere som Lagrange og Laplace var skeptiske. Fouriers ideer ble derfor først publisert i 1822 i hans hovedverk "Theorie analytique de la chaleur". Da teknikkene først var publisert, fikk de raskt stor utbredelse, og idag er Fourier-rekker og Fourier-transformasjoner hovedverktøy både i ren og anvendt matematikk.
Fourier var mest opptatt av de praktiske anvendelsene av sine resultater. At de ikke var fullstendig bevist, brydde han seg lite om, men det ergret ham at andre kviet seg for å bruke teknikker som virket så utmerket i praksis. På slutten av sitt liv uttalte han seg negativt om matematikere som Abel og Jacobi som arbeidet med teoretiske problemer fremfor å vie seg til de praktiske konsekvensene av varmeledningsteorien.
Fourier døde i Paris i 1830.
Del på Facebook
Begrep
-
Cosinus
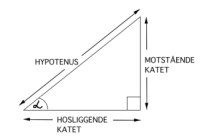
Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus. -
Fourier-rekker
Uendelige rekker av sinus og cosinus funksjoner som brukes til å beskrive og regne med periodiske funksjoner.
-
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.













