Pappus av Alexandria

Pappus av Alexandria
Pappus av Alexandria er den siste av de store greske geometerne, og et av hans teoremer regnes som fundamentet for den moderne projektive geometrien.
Vår viten om Pappus' liv er nesten lik null. Han ble født i Alexandria, og levde antagelig der hele livet. Pappus' store verk innen geometri er "Synagoge" eller "Mathematical Collection", som er en samling av matematiske tekster i åtte bøker som man tror ble skrevet rundt 340 (selv om noen historikere tror at Pappus hadde fullført arbeidet innen 325 e.Kr.).
Bok I og II dekker aritmetikk. Bok III inneholder et bevis for at de fem regulære polyedre kan innskrives i en sfære. Bok IV inneholder egenskaper til kurver inkludert spiralen til Arkimedes. I Bok V diskuterer Pappus de tretten semiregulære polyedre oppdaget av Arkimedes. Han beviser et sitat av Zenodorus om at sfæren har større volum enn hvilket som helst regulært legeme med samme overflateareal. Han beviser også det beslektede resultatet om at, for to regulære polyedre med samme overflateareal, har den med det største antall flater det største volumet. Bok VI og VII kommenterer bøker av andre forfattere (Theodosius, Autolycus, Aristarchus, Euklid, Apollonius, Aristaeus og Erathostenes).
Det er i Bok VII at Pappusproblemet dukker opp. Dette problemet hadde stor innvirkning på utviklingen innen geometri. I Bok VIII tar Pappus for seg mekanikk. Arbeidet viser ikke så mye originalitet, men det viser at Pappus hadde dyp forståelse for en rekke matematiske temaer, og at han mestret alle de viktigste tilgjengelige matematiske teknikkene.
Del på Facebook
Begrep
-
Arkimedes' spiral
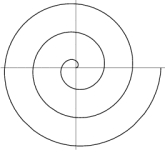
Spiralkurven er grafen til funksjonen (i polarkoordinater) r =v , der r er avstand til sentrum, og v er vinkelen mellom posisjonsvektor og positiv x-akse. Funksjonen kan også skrives som (kartesiske koordinater).
-
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
-
Pappus-problemet
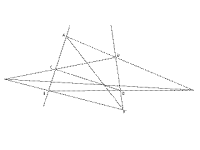
Pappus' problemet ble vist av Pappus og kalles derfor Pappus' setning. Denne setningen har spilt en viktig rolle i utviklingen av geometri, og da særlig analytisk og projektiv geometri.
Pappus' setning sier at dersom hjørnene til en sekskant ABCDEF ligger vekselvis på to linjer, vil skjæringspunktene mellom diagonalene også ligge på linje. -
Projektiv geometri
En gren av geometrien som ble utviklet på 1700- og 1800-tallet. Delvis inspirert av perspektivtegning, og er en utvidelse av Euklids plan- og romgeometri som tar med uendelig fjerne punkter. Dermed er parallelle linjer i planet linjer som møtes i et uendelig fjernt punkt.
-
Regulære polyedre
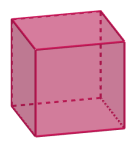
Polyedre der alle sideflatene er like og alle vinklene er like store. Kalles også Platonske legemer. Det finnes nøyaktig fem forskjellige: Tetraeder, heksaeder (kube), oktaeder, dodekaeder og ikosaeder.
-
Semiregulære polyedre
Polyedre der alle sideflater er regulære mangekanter, og alle hjørner er like.
Se Platonske legemer









