Cavalieris prinsipp

I denne teksten ser vi på romfigurer og volumet deres. Til dels må vi også se på flate figurer og deres areal. Vi skal først se på enkle figurer som rette prismer og kuber, deretter også på legemer som kan ha krumme overflater. Denne typen matematikk krever vanligvis en viss mengde infinitesimalregning. I infinitesimalregningen utvikler man metoder for å hanskes med uendelig små eller uendelig store størrelser, dvs. ganske avanserte og noe abstrakte metoder og symboler som det kan være trettende og vanskelig å komme inn i.

Bonaventura Cavalieri utviklet på 1600-tallet en måte å beregne volumer og arealer på som innholder mye av disse infinitesimale metodene, men på en intuitiv måte. Ved hjelp av hverdagslige forestillinger som ikke trenger noen videre utdyping og som er opplagte selv for elever på mellom- eller ungdomstrinnet, er det mulig å utvikle kunnskap om kompliserte romfigurer. Derfor ønsker jeg å blåse liv i denne gammeldagse metoden, som heter Cavalieris prinsipp.

Eksperimentér

Ingredienser:

2 like kortstokker, et memoryspill, en bunke med like visittkort
en stabel med kronestykker

Vi legger kortstokken foran oss på bordet. Den forestiller et rett, firkantet prisme med et visst volum. Til sammenlikning legger vi kortstokk nummer to ved siden av. Selvsagt har begge samme volum. Vrir vi litt på den ene kortstokken, kan vi lage flotte krumme romlegemer som ikke lenger behøver å være rette prismer. Men én ting kan vi si med sikkerhet om den nye romfiguren. Volumet må være det samme som i den første. Vi kan nemlig tenke oss hele kortstokkvolumet delt opp i små "skiver", nemlig kortene, som hver har et bestemt volum. Summen av dem utgjør hele volumet. Siden delvolumene i de to figurene vi sammenlikner er parvis like, må også totalvolumet være det samme. Plasseringen, vridningen og retningen av det enkelte kortet spiller her ingen rolle. Argumentet som Cavalieri brukte var litt forskjellig. I et senere avsnitt skal vi se nærmere på det. En stabel med memorykort eller kronestykker gjør forresten samme nytten.

Det samme eksperimentet kan vi nå gjennomføre med visittkortene våre. Vi kan lage både skjeve og vridde tårn, men volumet vil alltid være det samme. Har vi noen foreldete visittkort liggende, kan vi skjære stabelen over og sette sammen de to delstablene som vi da får på en ny måte. Volumet er fortsatt uforandret selv om formen på sammenlikningsflatene i hver ”etasje” er forskjellige. Men arealet er det samme i hver etasje. Konklusjonen er at formen på snittflaten ikke spiller noen rolle bare arealet i begge figurene er det samme.

Til nå har det vært slik at alle romfigurer vi har sett på har et konstant snittareal uavhengig av snitthøyden. Vi lager derfor nå et tårn med pappbiter av minkende størrelse som vi klipper ut og stabler oppå hverandre slik at de største bitene kommer nederst. Til hver pappbit lager vi nå en makker, altså en pappbit med samme areal men gjerne i en helt annen fasong, og stabler også disse bitene oppå hverandre. Igjen vil volumene av tårnene måtte stemme overens siden delene som brukes har samme volum.

Det viktigste ved Cavalieris prinsipp er følgende fire observasjoner:

Plasseringen av ”skivene” i hver etasje er likegyldig.
Formen på snittflaten i hver etasje er likegyldig.
Arealet må gjerne variere fra etasje til etasje.
Hvis arealet (altså måltallet for flateinnholdet) er det samme i begge sammenlikningsfigurene i alle etasjer, så har figurene samme volum.

Denne innlysende ideen om at romlegemer som kan tenkes bygd opp av like store deler må ha like stort volum, ble forfinet av Cavalieri. Han delte sine figurer opp i finere og finere snittskiver. Til slutt så han bare på snittflatene som ikke lenger hadde noen tykkelse. Disse kalte han "indivisibiles". Hvis nå to romlegemer ga like store snittflater når man skar over legemene i samme høyde over grunnflaten, og hvis dette var tilfelle for alle høyder, ja så måtte figurene ha likt volum. Dette kalles for Cavalieris prinsipp. (Cavalieris tankegang var nok en smule forskjellig fra denne framstillingen, men i moderne terminologi kunne man beskrive hans ideer slik).

Teori

Med Cavalieris prinsipp viser det seg at man med utgangspunkt i relativt enkle romfigurer plutselig kan få has på adskillig mer kompliserte legemer som vi i utgangspunkt aldri hadde trodd vi skulle kunne hanskes med. Som utgangsfigurer tar vi de klassiske romlegemene som var kjent allerede for grekerne i antikken, og som dermed også var velkjent for Cavalieri. Disse figurene er følgende.

Firkantet og trekantet prisme.

Volumet til hver av figurene beregnes ved hjelp av formelen $V = G \cdot h$ , der V betegner volumet, G grunnflaten og h høyden av figuren. Den neste grunnfiguren som vi forutsetter som kjent, er kilen.

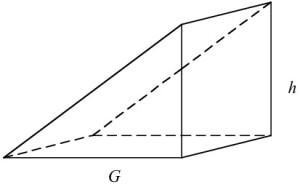
Kile.

Her er volumet bestemt av følgende formel: $V = \frac{G \cdot h}{2}$ .

Det er lett å se at to kiler vil kunne settes sammen til et firkantet prisme, og volumformelen er dermed lett å forstå. Kilen kan også sees på som et prisme hvis vi tar trekanten som grunnflate. Volumet blir det samme.

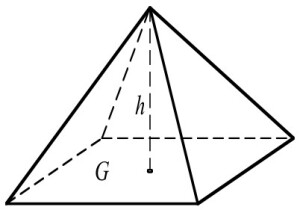
Den siste grunnformen er pyramiden, der volumet beregnes slik: $V = \frac{G \cdot h}{3}$ .

Pyramide.

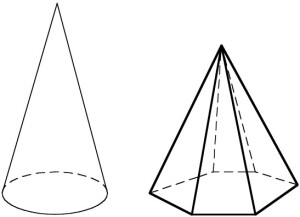
Her er det ikke så lett å se at tre pyramider kan settes sammen til et prisme. Denne problemstillingen kan de som er interesserte jobbe med i undervisningsopplegget som "hører til" denne teksten. I opplegget finner vi at grunnflaten kan være en hvilken som helst flate med krum rand. Hvis snittflaten i høyde h over grunnflaten er en formlik utgave av grunnflaten og flateinnholdet minker kvadratisk med høyden, så er formelen fortsatt korrekt.

Kjegle og pyramide med generell grunnflate.

I dette avsnittet godtar vi bare de ovennevte formlene for volumberegningen, slik at vi nå rår over de tre klassiske grunnformene; prisme/sylinder, kile og pyramide/kjegle. Dette utgjør vårt verktøyskrin i denne sammenhengen. Ved hjelp av disse verktøyene skal vi nå undersøke mer kompliserte og overraskende romlegemer.

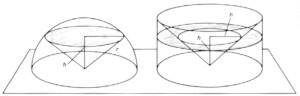
Det første nye eksemplet vi skal se på, er volumet av en kule. Vi tenker oss først en halvkule plassert med snittflaten på et plan. Sammenlikningsfiguren vår er en sylinder med samme grunnflate og høyde som halvkulen, der vi har fjernet en kjegleaktig del slik som tegningen viser. Kjeglen står på hodet, slik at spissen ligger i grunnplanet, mens kjeglens grunnflate er sammenfallende med "lokket" på sylinderen.

Kulen, sylinderen og kjeglen.

I tegningen har vi lagt inn en snittflate som skjærer både halvkulen og den andre romfiguren i en høyde h over grunnplanet. Arealet av snittfigurene er nå lett å beregne.
Ved hjelp av Pytagoras’ setning beregner vi arealet til snittflaten med halvkulen slik: $A = π \cdot s^{2} = π \cdot (r^{2} - h^{2})$ , men sammenlikningsfiguren gir det samme snittflateareal siden sylinderen har radius r, mens snittet gjennom kjeglen har radius h der snittplanet skjærer gjennom den. Dette er tilfelle fordi kjeglens rand har en stigning på 1, eller 45°. Dette gjelder uavhengig av hvilken høyde h vi velger for snittflaten. Ifølge Cavalieris prinsipp må nå volumene av romfigurene være de samme. Volumet av sammenlikningsfiguren, som er en sylinder som mangler en kjegleformet kjerne, er nå lett å beregne ved hjelp av to av de tre klassiske grunntypene som vi har beskrevet ovenfor. For å finne kulens volum må vi doble halvkulens.

$V = 2 (π \cdot r^{2} \cdot r - \frac{π \cdot r^{2} \cdot r}{3}) = \frac{4 \cdot π \cdot r^{3}}{3}$

På en liknende lett måte kan vi nå beregne både ellipsoider, hyperboloider og paraboloider.

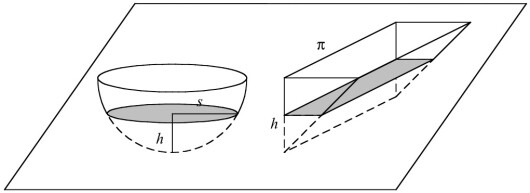
La oss begynne med paraboloiden, som vi kan tenke oss kommer fram når en parabel $y = x^{2}$ snurrer rundt sin symmetriakse.

Paraboloide.

Snittflaten i paraboloiden har areal $A = π \cdot s^{2} = π \cdot x^{2} = π \cdot y = π \cdot h$ , der vi la snittet ved høyden h. Sammenlikningsfiguren er denne gangen en kile med bredde $π$ og stigning 1, dvs. en vinkel på 45° i spissen. På den måten får begge figurene samme snittareal, og Cavalieris prinsipp sikrer oss at volumet er det samme, nemlig $V = \frac{π \cdot h^{2}}{2}$ .

Til slutt prøver vi å finne volumet av en ring med sirkelformet tverrsnitt. Vi tenker oss at ringen framkommer ved å rotere en sirkel med radius r om en akse med avstand R fra sirkelens sentrum.

Ring, kalles også ofte for torus.

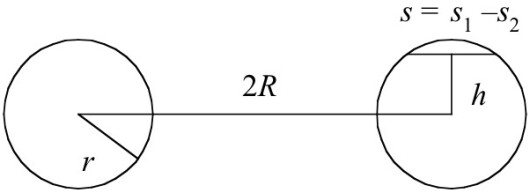
Vi legger nå ringen på et plan og snitter den med et nytt plan parallelt med det første. Snittfalten blir en "ringflate", alstå en sirkel med sirkelformet hull. De to radiene betegner vi med $s_{1}$ og $s_{2}$ . Arealet kan beskrives på følgende måte:

$A = π \cdot (s_{1}^{2} - s_{2}^{2}) = π \cdot (s_{1} - s_{2}) \cdot (s_{1} + s_{2}) = 2 \cdot π \cdot R \cdot (s_{1} - s_{2})$

I formelen inngår R, som er konstant (dvs. uavhengig av høyden der snittet foretas), og størrelsen $s = (s_{1} - s_{2})$ , som kan tolkes som lengden av en sekant hvis avstand fra senteret er h.

Snitt gjennom ringen.

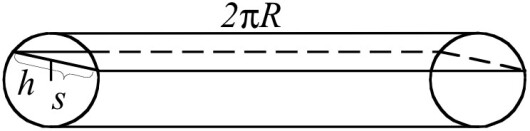
Til sammenlikning tenker vi oss en sylinder med høyde $2 \cdot π \cdot R$ og med sirkelformet tverrsnitt, der radius er r. Sylinderen står ikke på grunnplanet, men ligger der som et rør.
Snittflaten blir her et rektangel med sider $2 π R$ og s. Arealet blir derfor $A = 2 π R s$ , der s er lengden av korden med avstand h fra senteret. Det betyr at ringen har samme volum som en sylinder med samme tverrsnitt og lengden lik omkretsen av en sirkel som kan tenkes å gå midt gjennom ringen, altså $V = 2 \cdot π \cdot R \cdot π \cdot r^{2} = 2 π^{2} r^{2} R$ .