Pascals trekant
I Europa har denne trekanten bestående av (uendelig mange) rader av tall fått navn etter den franske matematikeren Blaise Pascal, men både kineserne og araberne kjente til talltrekanten lenge før Pascal.
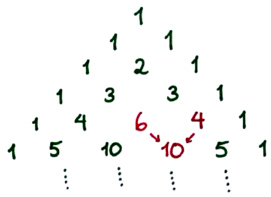
Figur 1: De seks første radene i Pascals trekant.
Pascals trekant er uendelig mange rader av tall som, danner en (uendelig) trekant. Trekanten bygges opp ved å sette 1-ere på kantene, og la hvert tall innenfor 1-erne være summen av de to tallene i raden over som er på hver side av tallet. For eksempel får vi tallet 10 i rad 5 (det øverste 1-tallet er rad 0) ved å legge sammen 4 og 6, som vist i figur 1. Neste rad i figur 1 blir derfor 1, 1+5, 5+10, 10+10, 10+5, 5+1, 1, altså 1, 6, 15, 20, 15, 6 og 1.
Blaise Pascal genererte trekanten på en litt annen måte når han først publiserte sine ideer om dette i 1665. Han så på en (uendelig) firkant med tall, figur 2:
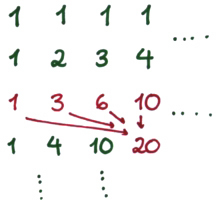
Figur 2: Pascal satte opp sammenhengen i en firkant.
Øverste rad består igjen av 1-ere. Hvert av de andre tallene i firkanten fikk han ved å ta summen av alle tallene som ligger i samme posisjon og i posisjonene til venstre for tallet i raden over. For eksempel får vi tallet 20 i rad 4 ved å legge sammen 1, 3, 6 og 10 i raden over, som vist på tegningen. De fire første tallene i neste rad blir 1, 1+4, 1+4+10 og 1+4+10+20, altså 1, 5, 15 og 35. Diagonalene nedover mot venstre i firkanten gir radene i Pascals trekant.
I Europa har altså trekanten vi startet med fått navnet Pascals trekant, men vi nevner at både kinesiske og arabiske matematikere kjente til arrangementet av disse tallene lenge før Blaise Pascal. I Kina kalles trekanten Yanghui-trekanten. Uansett, trekantens tall dukker opp i mange sammenhenger, og trekantformen er en nyttig måte å holde orden på disse tallene. For eksempel fins fibonaccitallene blant trekantens tall.
Hovedbruksområdene for Pascals trekant er algebra og kombinatorikk. Begge områdene gjør bruk av at tallene i Pascals trekant er binomialkoeffisienter
der n er radnummeret, n ≠ 0, og k er posisjonen i raden.
For eksempel er tallene i 5. rad 1, 5, 10, 10, 5, og 1, som er henholdsvis binomialkoeffisientene
.
Formelen for en binomialkoeffisient er
der og 0!=1
I kombinatorikk dukker disse tallene opp veldig ofte. Binomialkoeffisienten gir oss nemlig antall forskjellige måter å trekke k ting fra en mengde av n ting på. I algebra dukker de opp som koeffisienter når vi regner ut potenser av polynomer med to ledd. For eksempel er
.
På http://mathforum.org kan du utforske Pascals trekant. Du kan gjøre mye rart med den. For eksempel viser det seg at det første tallet etter 1-eren i hver rad er en faktor i de andre tallene ≠ 1 i raden hvis, og bare hvis, tallet er et primtall. Du kan også se hvordan trekanten dukker opp i konstruksjonen av regulære polygoner, og i forbindelse med Sierpinski-trekanten. Vi skal se litt nærmere på det sistnevnte.
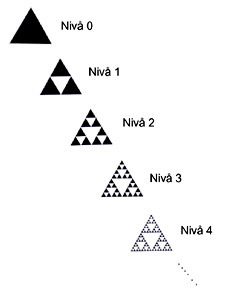
Sierpinski-trekanten hører inn under en klasse matematiske objekter kalt fraktaler. Vi kan konstruere Sierpinski-trekanten, som ble konstruert av Waclaw Sierpinski i 1915, ved å starte med en likesidet trekant (nivå 0). Trekk deretter streker mellom midtpunktene på de tre sidene slik at du får fire like store trekanter i den store trekanten (alle er formlike). Så lager du et hull i den store trekanten ved å fjerne det indre av den midterste trekanten. Nå har du nivå 1 i konstruksjonen av Sierpinski-trekanten. For å få nivå 2, gjentar vi nivå 1 på hver av de tre trekantene vi har igjen. Når denne prosessen gjentas uendelig mange ganger, blir resultatet Sierpinski-trekanten. I figur 3 ser vi konstruksjonen opp til nivå 4:
Figur 3: Sierpinski-trekanten til nivå 4.
Vi ser at vi lager neste nivå ved å erstatte en trekant med tre like store mindre trekanter, slik at alle er formlike (alle er likesidede, og lengden på sidene halveres for hvert nivå). Antall trekanter blir dermed tredoblet fra et nivå til det neste. Sierpinski-trekanten inneholder altså uendelig mange likesidede trekanter: Uansett hvor mye vi forstørrer Sierpinski-trekanten, kommer det nye slike trekanter til syne.
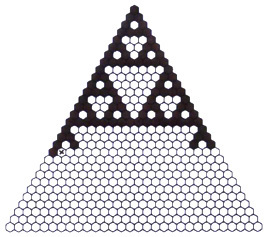
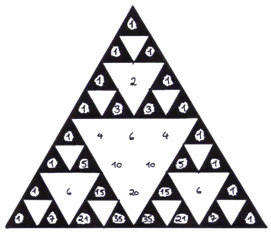
Hvordan kan vi lage Sierpinski-trekanten fra Pascals trekant? En måte er å bruke regulære sekskanter som utgangspunkt: Vi tegner like store sekskanter rundt alle tallene i Pascals trekant, og setter dem inntil hverandre slik at vi får en trekant (med litt "ruglete" kanter). Deretter fargelegger vi alle sekskantene der det står et partall med en farge, og oddetalls-sekskantene med en annen farge (vi sier at vi fargelegger Pascals trekant modulo 2). I figur 4 har vi gjort fargeleggingen for de 19 første radene med svart for oddetall og hvitt for partall:
Figur 4: Pascals trekant rammet inn av sekskanter hvor alle oddetallene er farget mørkt og alle partallene er hvite.
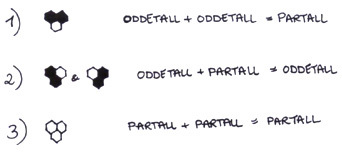
Legg merke til at vi har fjernet tallene, da vi egentlig ikke trenger dem: Vi vet at vi har 1-ere på kantene og i de to første radene, så disse sekskantene blir svarte. Dessuten vet vi hvordan trekanten er bygd opp; hvert av tallene er summen av de to tallene i raden over som er på hver side av tallet. Dermed kan vi fargelegge trekanten ved å bruke følgende tre mønstre:
Den øverste sekskanten representerer den likesidede trekanten vi startet med i konstruksjonen av Sierpinski-trekanten. De 4 øverste radene med sekskanter / tall i Pascals trekant gir oss første nivå i Sierpinski-trekanten, de 8 øverste radene gir oss andre nivå, og hvis du fortsetter fargeleggingen ved å bruke de tre mønstrene, ser du at de 16 øverste radene gir tredje nivå, osv. Sekskanten med et kryss i figur 4 er forøvrig binomialkoeffisienten , som er et oddetall.
For å få vekk de "ruglete" kantene i tegningen over, kan vi bruke regulære trekanter (likesidede) istedenfor regulære sekskanter, men for at puslespillet skal passe sammen nå, får vi hvite trekanter snudd opp-ned mellom alle tallene. Vi farger trekantene med oddetall svarte og får resultatet som vist i figur 5:
Figur 5: Pascals trekant innrammet med trekanter.
Del på Facebook
Eksterne lenker
-
Interaktiv Pascal-trekant
Her kan du teste Pascals' trekant og se hvordan den blir hvis du bytter ut antall rader.(mathforum.org)