Palindromer

Vi er kjent med at geometriske former kan være symmetriske på ulike måter. Men ord kan også sees på som symmetriske. Vi kan kalle et ord symmetrisk hvis det blir det samme ordet enten du leser fra venstre mot høyre eller fra høyre mot venstre. Navnet ANNA er et slikt eksempel. Ordet RADAR er et annet. Slike ord kalles palindrom. Ser vi på ordet INNI, er det symmetrisk på enda en måte. Det blir nemlig det samme enten vi leser det forfra eller bakfra eller opp ned (altså geometrisk snur bokstavene opp ned).

Tall kan selvfølgelig også være palindrom. Noen er dessuten symmetriske både bak-fram og opp-ned, slik som for eksempel

1888081808881

Dette palindromet er dessuten et primtall!

Det er ikke uten grunn at jeg velger å skrive om palindromer nettopp i Abelåret 2002. Ikke fordi Niels Henrik Abel arbeidet med palindrom, men fordi tallet 2002 er et palindrom. Sist det var et palindromår var i 1991. Kanskje det ikke er så sjelden? Da tar du feil. Det er MEGET uvanlig at det er to palindromår i løpet av et menneskes liv. Sist gang det var så kort avstand mellom var i 999 og 1001. Neste gang er i 2992 og 3003. Så det skjer ca hvert 1000. år. Neste gang det er et palindromår er i 2112. Det finnes dessuten en helt spesiell dato dette året, som er et større palindrom: den 20. februar, og hvis vi i tillegg tar med klokkeslettet 20:02, blir det enda mer spesielt, og særlig hvis vi kutter ut tegnene:

2002 2002 2002

I det magiske kvadratet nedenfor får vi summen 2002 enten vi summerer vannrett, loddrett eller diagonalt.

494	501	500	505
508	497	502	495
501	496	507	498
499	506	493	504

 

Da vil vi selvsagt som nysgjerrige matematikere begynne å lure på: Hvor lenge er det siden sist vi hadde et slikt fenomen, med klokkeslett, dato og år som dannet et tredobbelt palindrom? Svaret er klokka 11:11, den 11.11 år 1111. Hvis vi ikke krever tredobbelt palindrom, har vi også klokka 12:21 den 21.12 år 1221. Det blir

1221 2112 1221

Men hvis vi skriver datoen som i USA, med måned før år, blir det et tredobbelt palindrom:

1221 1221 1221

Neste gang blir klokka 21:12 den 21.12 år 2112. Etter dette vil det aldri skje igjen, for klokka går bare til 24 og vi har bare 12 måneder.

Men nå er det slik at nesten alle tall kan forvandles til palindromer. Hvis vi for eksempel tar for oss årstallet neste år: 2003. Så snur vi det bak-fram til 3002 og legger sammen de to tallene. Da får vi 5005 som er et palindrom. Det gikk jo fort. Men hva hvis det ikke er to 0-er som de midterste sifrene? Ta for eksempel 2318. Snu det og legg sammen. Det blir 2318 + 8132 = 10450. Snu og legg sammen: 10450 + 5401 = 15851. Kan vi alltid holde på å snu og legge sammen, og få et palindrom bare vi holder på lenge nok? Det vet vi faktisk ikke! Dette er et av de uløste problemene i tallteori. Vi vet ikke om tallet 196 kan bli et palindrom!

Men om vi følger prosedyren: Ta et hvilket som helst helt tall med to siffer eller mer. Bytt om rekkefølgen på sifrene, slik at det siste blir først, det nest siste nummer to osv. og summer dette tallet med det opprinnelige. Hvis svaret du får ikke er et palindrom gjentas prosessen helt til du ender opp med et palindrom.

 

 

Tallet 196 er det minste hele tallet som muligens ikke ender opp i et palindrom.

Av de 900 3-sifrede tallene som finnes, er 90 palindromer. 735 3-sifrede tall må ha 1 til 5 gjentakelser med omvending og addisjon. Av de siste 75 3-sifrede tallene, vil de fleste til slutt ende i et palindrom. Blant disse er 187, 286, 385, 583, 682, 781,869, 880 og 968. Men for eksempel tallene 196, 887, 1675, 7436, 13783 vet vi ikke om vil ende opp i et palindrom. Til nå har letingen endt opp i tall med mer enn 27 millioner siffer, men det har altså ennå ikke endt opp i et palindrom. De som synes det er morsomt å finne noen som tar lang tid, kan prøve med 10911. Det tar 55 gjentagelser og ender med palindromet

4668731596684224866951378664.

Oppgave:
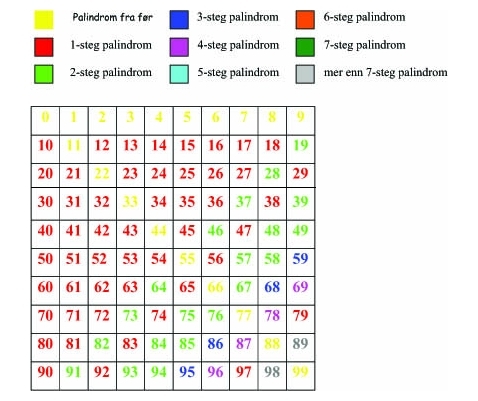
Fargelegg tallene i 0-99-kartet slik at det viser hvor mange steg som skal til før tallet du starter med er gjort om til et palindrom!

Nedenfor har jeg laget et forslag til hvordan det kan se ut når det er ferdig utfylt.

Eksempel:
1. 69+96=165     2. 165+561=726     3. 726+627=1353         4. 1353+3531=4884

PALINDROM I ET 0-99 KART

Hvilke farger bruker du? Fargelegg de små kvadratene for å vise hva fargene betyr:

Finnes det trekanttall som er palindromer?

 

Det er 40 palindromer blant de 10 000 000 første trekanttallene. Det tiende trekanttallet, 55, er det minste palindromet blant denne tallmengden. Det neste er nummer 11, som er 66. Både trekanttall nummer 11 og 111111 er palindromer, men så er det slutt på systemet, for trekanttall nummer 11111111 er ikke et palindrom. Trekanttallene er på formen 1, 1+2, 1+2+3, 1+2+3+4, osv., så de 11 første trekanttallene er 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66.

Vi kan også tenke på regnestykker eller tallsetninger som palindromer:

 

Regnestykker som er palindrome.

Nedenfor finner du ideer til oppgaver. Legg merke til mønsteret etter hvert som du regner.

 

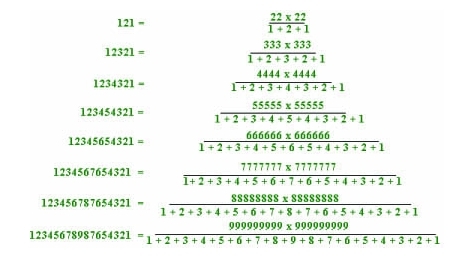
Palindrome brøker som gir palindrome heltallssvar.

 

Det finnes mange forskjellige mønstre og sammenhenger som er spennende å lete etter. Vi blir veldig fascinert av slike mønstre og denne fascinasjonen gjør at vi gjerne bruker tid på utforsking. Matematisk har også dette større verdi enn bare å øve på tallregning. Det handler om å finne mønster og system, og ikke minst opparbeide en god tallfølelse.

Prøv med følgende tall:
11, 11² , 11³, 11⁴, 101, 101² , 101³ , 1014⁴, 1001, 1001² , 1001³ , 1001⁴

En annen morsom sammenheng er denne:
Start med 121. Del på 11. Det gir 11. Del på 11 igjen. Det gir 1.
Gjør det samme med 1234321. Det gir palindromene 112211 og 10201.

Forsøk med 12345654321 og 123456787654321!

8 x 8 + 13 = 77
88 x 8 + 13 = 717
888 x 8 + 13 = 7117
Fortsett videre!

Primtall kan også være palindromer. Første ramme viser tre eksempler på at tre etterfølgende primtall har en sum som er palindrom. Alle tallene i nederste ramme er primtallspalindromer.

 

Tre etterfølgende primtall har palindrom sum (tre eksempler). Alle tallene i denne rammen er primtallspalindromer.