Tallet i

Hvilke tall x passer inn i ligningen $x^2+x+1=0$ ?

Hvis vi bruker formelen for løsning av en andregradsligning, får vi et negativt tall under et rottegn. Når dette skjer blir vi på skolen ofte bedt om å skrive "Ingen løsning".

Hva betyr det at ligningen har "Ingen løsning"? Det betyr at vi ikke har noen tall som passer inn i ligningen blant de tallene vi kjenner til (de reelle tallene). Men "Ingen løsning" er ingen tilfredsstillende løsning, så vi må utvide tallbegrepet vårt slik at tallene som er roten av negative tall også får sin naturlige plass. Når vi har gjort det, viser det seg at vi har alle tall vi trenger for å løse polynomligninger! Tallet i spiller hovedrollen i denne utvidelsen, og vi skal nå se litt nærmere på dette:

De gamle greske matematikerne måtte også utvide sitt tallbegrep: Som vi har vært inne på i andre artikler regnet de gamle grekerne med lengder og forhold mellom dem. Grekerne trodde derfor lenge at alle tall kunne skrives som et forhold mellom positive hele tall, altså at de var rasjonale. Men så oppdaget de tallet vi kaller $\sqrt{2}$. Ved Pytagoras' setning er det lengden av hypotenusen i en rettvinklet likebeint trekant der katetene er av lengde 1. Etter hvert innså man at dette ikke er et rasjonalt tall, og at det derfor fantes andre tall enn de rasjonale. De nye tallene ble kalt irrasjonale. Skrevet som en ligning skulle altså grekerne løse $x^2=2$ , og løsningen fantes ikke blant tallene de kjente til.

Hva om vi skal løse ligningen x + 3 = 1 ? Da trenger vi et negativt tall. I artikkelen om tallet null så vi at araberne satte opp regneregler for null og negative tall slik at de passet inn med de positive tallene. Da matematikken "gjenoppsto" i Europa på 1200-tallet, tok det likevel lang tid før de negative tallene ble akseptert, akkurat som det tok tid å akseptere de irrasjonale tallene.

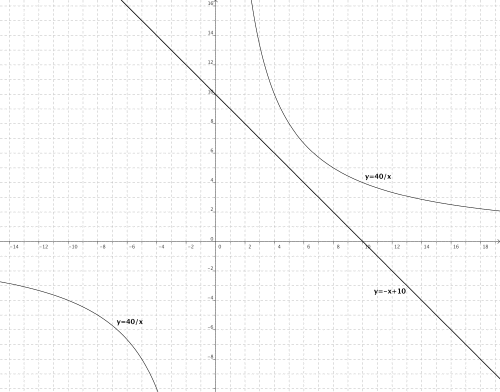
Og historien gjentar seg: I "Ars Magna" fra 1545 prøver Girolamo Cardano å løse ligningssystemet

$x+y=10$

$xy=40$

Hvis vi prøver å finne en løsning på dette ligningssystemet geometrisk, kan vi tegne kurvene i det reelle planet:

Vi ser at vi ikke har noen reelle tall som løsning (ingen skjæringspunkter mellom kurvene). Cardano løste imidlertid ikke ligningssystemet geometrisk, men algebraisk, og fikk løsningene $x=5+\sqrt{(-15)}$ og $x=5-\sqrt{(-15)}$ . Dette var første gangen at roten av et negativt tall dukket opp.

Det største tallsystemet man hadde på Cardanos tid var det vi i dag kaller de reelle tallene. De reelle tallene er et større tallsystem enn for eksempel de hele tallene siden de reelle inneholder de hele, og i tillegg (uendelig) mange ekstra tall. Cardano antok at røttene av negative tall fulgte de samme regnereglene som tallene han kjente til, og på den måten sjekket han at løsningen han hadde fått faktisk var en løsning ved innsetting i ligningssystemet. Han manipulerte også løsningene av en kubisk ligning som involverte $\sqrt{(-121)}$ på tilsvarende måte, men han innså ikke at dette var starten på noe stort.

I sin bok "Algebra" (1572), manipulerte Raphael Bombelli Cardanos uttrykk slik at Cardanos løsning av $x^3=15x+4$, nemlig $x={(2+\sqrt{(-121)})}^{\frac{1}{3}}+{(2-\sqrt{(-121)})}^{\frac{1}{3}}$ , ble x = 4. Dette var det første hintet om at disse nye tallene kunne bli nyttige for å løse reelle matematiske problemer.

Etter Bombelli fulgte en del år der man fortsatt regnet og manipulerte med roten av negative tall som om de var "vanlige" tall. I dag bruker vi tallet i om roten av −1. Ved å multiplisere i med positive og negative tall (de tallene vi hadde før vi innførte i), får vi nye tall som er slik at kvadratet av hvert av tallene er et negativt tall. Disse nye tallene ble kalt imaginære tall, og de man allerede hadde ble kalt reelle tall. Det var Rene Descartes som først skilte mellom reelle og imaginære tall (1637).

Mye av dagens matematiske notasjon stammer fra Euler, og igjen er det Euler som først bruker i om den imaginære enheten $\sqrt{(-1)}$ . Han oppdaget også flere formler, bl.a. $e^{i\pi }=-1$ (i 1748). Euler var en matematiker med stor innflytelse. Han talte varmt for bruken av imaginære tall, og mot slutten av 1700-tallet var det mange matematikere som brukte tall på formen $x+yi$ . Her er x et reellt tall (den reelle delen) og yi et produkt (den imaginære delen) der y er et reellt tall og $i^2=-1$ .

Det ble også vanlig å representere tallene $x+yi$ som punkter i (x,y)-planet, der den reelle delen var plassert på x-aksen, og den imaginære delen på y-aksen. For eksempel er tallet i punktet som ligger en enhet rett opp fra origo, på y-aksen. Det var flere som oppdaget denne geometriske tolkningen. Blant dem var Wessel, Argand og Gauss, som alle jobbet med dette rundt århundreskiftet 17-1800. John Wallis representerte tallene  $x+y\sqrt{(-1)}$ geometrisk allerede i 1673, men av en eller annen grunn ble dette ignorert.

Vi kan altså tolke de reelle tallene som 1-dimensjonale tall som ligger på en linje (x-aksen / tallinjen), og tallene $x+yi$ , som etter hvert ble hetende komplekse tall, som 2-dimensjonale tall liggende i (x,y)-planet. Vi ser dermed hvorfor vi ikke kan se løsningen av Cardanos ligningssystem i det reelle bildet vi tegnet: Løsningen er paret (x,y), der både x og y er 2-dimensjonale tall. Dermed er det to ekstra dimensjoner som ikke kommer frem i det reelle bildet.

Utviklingen av matematikken frem mot slutten av 1700-tallet hadde altså sett en stadig utvidelse av tallbegrepet, fra de positive hele tallene til de reelle og imaginære tallene. Man kunne nå løse ligninger der man hadde roten av negative tall, for eksempel var  $\sqrt{(-15)}$  tallet  $\sqrt{15}$ multiplisert med i, som igjen var punktet $\sqrt{15}$ enheter opp fra origo på y-aksen i (x,y)-planet. Det store spørsmålet var nå om det fantes flere ligninger der koeffisientene kunne være tall man kjente, men der man fikk løsninger som involverte tall man ennå ikke kjente?

Svaret ble gitt av Gauss i 1799: En polynomligning av grad n har n røtter, alle på formen $x+yi$ der x og y er reelle tall. Dette kalles algebraens fundamentalteorem, og det sier altså at vi ikke trenger flere tall enn tallene  $x+yi$ for å løse algebraiske ligninger (polynomligninger)! Fra nå ble tallene på formen $x+yi$ kalt komplekse tall (siden de er alle løsninger vi kan ha av algebraiske ligninger), og (x,y)-planet ble kalt det komplekse plan.

I 1837 publiserte William Rowan Hamilton dagens algebraiske definisjon av komplekse tall uten bruk av tallet i: De komplekse tall er mengden av ordnede par av reelle tall som følger visse regneregler. La (a,b) og (c,d) være komplekse tall. Da er a, b, c og d reelle tall og vi har

$(a,b)+(c,d)=(a+c,b+d)$
$(a,b)-(c,d)=(a-c,b-d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$
$\frac{(a,b)}{(c,d)}=(\frac{(ac+bd)}{t},\frac{(bc-ad)}{t})$ , der $t=c^2+d^2$

Vi har nå utvidet vårt tallbegrep: De komplekse tallene er et større tallsystem enn de reelle tallene; de komplekse inneholder de reelle og (uendelig) mange ekstra tall.