Sfærisk geometri

Når vinkelsummen er mer enn 180º

I riktig gamle dager trodde folk at jorda var flat og at sola på en eller annen måte ble heist over himmelen hver eneste dag. I dag vet vi selvfølgelig bedre: Vi lever på en rund klode som svever rundt i verdensrommet uten alt for mye mål og mening (?).

Plangeometrien som matematisk disiplin er svært gammel, faktisk blant de eldste delene av det som i dag går under samlebetegnelsen matematikk. Plangeometrien, eller læren om punkter, linjer, vinkler og figurer i planet, ble tidlig studert grundig og Euklid satte faktisk det hele i en ordentlig setting allerede for 2 500 år siden. Euklid var på jakt etter plangeometriens egenskaper, dvs. hvilke regler som gjelder og hva som skal til for å beskrive plangeometri.

Euklid definerte punkter og linjer og satte opp et sett av postulater, eller grunnsetninger, som skulle gi en komplett beskrivelse av geometrien. Det mest kjente av disse postulatene er det såkalte parallellpostulatet. Vi skal komme tilbake til det senere. Først skal vi se på noen av de egenskapene som beskriver geometri i planet. Her kunne vi brukt Euklids formuleringer, men det er lettere å sette seg inn i de mer moderne språklige versjonene. Beskrivelsen vil ikke være komplett, men kun gi et innblikk.

Vi trenger noen begreper, og vi har allerede nevnt punkter og linjer. En viktig egenskap ved en plangeometri er det at en rett linje deler planet i to. Det er kanskje ikke så merkelig, men det som er viktig er at dette er en egenskap som er spesielt for plangeometri. Det er lett å se at dette ikke gjelder for romgeometri, i rommet kan vi gå rundt linja fra den ene siden til den andre, det går ikke i planet. Vi må jo holde oss i planet og har ikke muligheten til å hoppe over linja til den andre siden. Vi skal også ta med en insidens-egenskap, nemlig det at hver gang vi har to punkter så finnes det en rett linje gjennom dem, og det finnes bare én slik linje. Husk at rette linjer går uendelig langt i hver retning og at definisjonen av en rett linje gjennom de to punktene er den korteste veien mellom de to punktene.

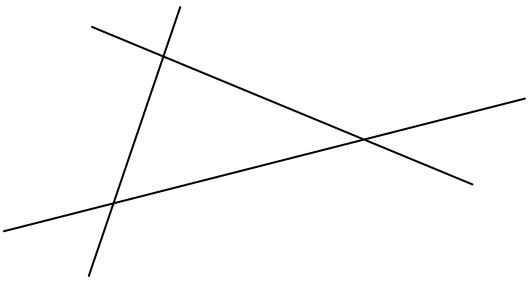
Et annet begrep som er viktig i geometri er vinkler. Når vi har to forskjellige rette linjer har vi to muligheter, enten er de parallelle, dvs. at linjene ikke har felles punkter, eller så møtes de i ett punkt. Dersom linjene har to punkter felles så er linjene like, slik vi har sett over. Men hvis vi nå tar for oss to rette linjer som ikke er parallelle, dvs. at de skjærer hverandre i ett punkt, så vil linjene ha en bestemt vinkel mellom seg. Det er mange måter å angi slike vinkler på, vi kan f.eks. bruke grader. En rett vinkel er da 90º, mens vinkelen går mot 0º når linjene blir mer og mer parallelle. Vi kan se på tre rette linjer som alle skjærer hverandre, men ikke i ett punkt. Det skal altså se sånn ut:

Tre rette linjer som alle skjærer hverandre, men ikke i ett punkt.

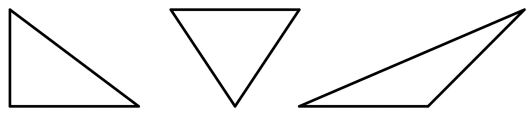
De tre linjene danner som vi ser en trekant. I hvert hjørne danner de to linjene som skjærer hverandre en vinkel, og på skolen lærer vi at summen av de tre vinklene alltid 180º. Dette er tilfellet, uansett hvordan trekanten ser ut. Hvis dere måler vinklene i disse trekantene vil dere få det samme svaret, 180º.

Alle trekantene har vinkelsum 180 grader.

Alt det vi har sagt til nå kan for mange fortone seg som opplagtheter, og det er også meningen. Det vi har gjort er bare å finne forskjellige egenskaper ved plangeometri som kan være med på å beskrive geometrien. Nå skal vi bevege oss fra planet og over til andre geometrier.

Innledningsvis nevnte vi at man en gang i tida risikerte å bli brent på bålet for å hevde at jorda var rund. Nå skal vi lage geometri på denne runde jorda, eller på alle andre kuler for den saks skyld. Det første problemet er de rette linjene. Det er jo ingen rette linjer på en kuleflate, vi vil jo at de skal følge overflaten og da blir de automatisk krumme. Men det vi mener med en rett linje på en kuleflate er egentlig det samme som vi mener med en rett linje i planet, nemlig den korteste vei mellom to punkter. Men denne gangen skal linjene følge overflaten og det er en bestemt linje som gir den korteste avstanden. Bare prøv. Ta en hyssingstump og strekk den langs en rund ball. Når den er helt stram har du funnet en rett linje på kuleoverflaten. Det viser seg at alle disse rette linjene vi får er deler av såkalte storsirkler. Storsirkler er sirkler som går rundt hele kula, akkurat som en ekvator.

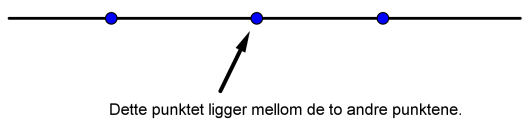
Når vi nå vet hva rette linjer på en kuleflate er kan vi begynne å kikke på forskjeller mellom kulegeometri og plangeometri. En morsom forskjell er det som ofte kalles mellomhet. Hvis vi har tre punkter på en rett linje i planet, så vil alltid en av dem ligge mellom de to andre.

Sirkel med tre punkter - alle punktene ligger mellom de to andre.

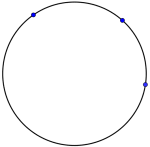
På en kuleflate har vi ikke denne egenskapen. Husk at en rett linje er en storsirkel rundt hele kula. Et hvilket som helst av tre punkter på en linje ligger mellom de to andre.

Neste egenskap vi tar for oss er parallelle linjer. Vi husker at i planet har vi to muligheter, enten er linjene parallelle eller så skjærer de hverandre i ett punkt. På en kuleflate, hvor de rette linjene er storsirkler har vi kun én mulighet. Hver gang vi plukker ut to linjer så vil de skjære hverandre, og de vil faktisk skjære hverandre i to punkter. Dette er altså helt annerledes enn i en plangeometri. Den siste forskjellen vi skal kikke på er vinkelsummen i en trekant. I planet er denne summen 180º, så hva er den på en kuleflate? Er den 180º, eller mer eller mindre? Vi kan ta et eksempel på jordoverflaten. De tre hjørnepunktene i trekanten er Nordpolen, og to punkter på ekvator. Vinkelen mellom en rett linje fra ekvator til nordpolen og ekvator er rett, dvs. 90º. Ekvator går jo rett øst-vest, mens en linje mot nordpolen nødvendigvis går nord-sør. Dette gjelder selvfølgelig for begge de to punktene på ekvator og vinkelsummen er derfor minst 90º+90º=180º. I tillegg kommer vinkelen mellom de to nord-sør-linjene opp på Nordpolen og denne vinkelen kan være hva som helst. Dermed får vi en vinkelsum som er større enn 180º. Og det får vi alltid på en kuleflate. Jo mindre trekanten er i forhold til kula, jo nærmere 180º er vinkelsummen, men uansett er den større enn 180º. Vi kan forklare det med at trekanten "buler" opp på midten og derfor får større vinkler. Man kan faktisk bruke denne egenskapen til trekanter til å fastslå at jorda er rund. Vi velger ut tre punkter på jordoverflaten, f.eks. i Kristiansand, i Hirtshals og i Newcastle og trekker de rette linjene mellom de tre byene (langs overflaten). Da får vi en trekant som rammer inn en stor del av Nordsjøen. Hvis vi måler vinklene i de tre byene og legger sammen får vi litt mer enn 180º... Det er bare å prøve.