Koordinatsystemer
Tenk om du var skipbrudden midt ute på havet og drev omkring på en liten flåte. Det eneste lyspunktet var at du hadde en radio slik at du kunne kommunisere med redningssentralen. Hva ville du si? "Her er jeg, kan dere plukke meg opp?" Redningssentralen ville selvfølgelig spørre om hvor du befinner deg, men det er vel tvilsomt om stedsangivelsen "På havet!" vil være tilstrekkelig til at redningshelikopteret kunne komme til unnsetning. På en eller annen måte måtte du oppgi din posisjon.
Hvis du hadde en klokke og mulighet til å måle solhøyde på ulike tidspunkt så ville du faktisk ha vært i stand til å beregne din posisjon med relativ stor presisjon, men det er ikke den type gammel sjømannsskap kombinert med matematikk vi skulle diskutere her, vi skal være mye mer grunnleggende.
Referansesystem
For i det hele tatt å kunne angi en posisjon trenger vi en eller annen form for referansesystem. Vår måte å bestemme posisjoner på er sånn sett relativ. Vi tar utgangspunkt i noe vi på en eller annen måte vet hvor er og en retning. Ved hjelp av dette referansepunktet, en gitt retning og en målestokk kan vi nå angi alle punkter på en plan overflate. For å ha en slik presisjon i rommet trenger vi nesten det samme, bare to retninger i stedet for én. Merk at dette i prinsippet er det samme som vi bruker i dagligtale, Et flott soppsted kan f.eks. være beskrevet ved: "Gå til stiskillet ved den store furua, rett nedenfor Hyggeligtoppen. Ta til venstre, rett inn i skogen og gå ca. 50 meter. Da kommer du til et sted med mye sopp:" I prinsippet er det det samme angivelsen vi bruker når vi snakker om punktet (1,1) i et rettvinklet koordinatsystem. Forskjellen er at den siste angivelsen er mer abstrakt. Vi må selv bestemme oss for hvor origo er, vi må selv plassere x-aksen og vi må selv bestemme oss for lengdeenheten. Når dette er gjort er stedsangivelsen entydig. Koordinatsystemer er funnet opp nettopp for dette formålet, å kunne gi en entydig og enkel beskrivelse av steder, enten på arket eller i naturen.
Kartesiske koordinater
Våre vanlige kartesiske (rettvinklede) koordinater er oppfunnet for på en enkel måte å kunne angi posisjon i en flat verden, hvor punktet (1,1) er det samme uansett hvilken rekkefølge vi beveger oss til koordinatene. Dette er ikke tilfelle på en sirkelflate. På en plan flate er det det samme om man går én meter i en retning og deretter i én meter i en annen som om man bytter om hvilken retning man går i først. Men hvis vi prøver oss på det samme på en kuleflate går det helt galt. Starter vi på et bestemt punkt på ekvator og beveger oss 1 000 km østover for deretter å bevege oss 1 000 km nordover så kommer vi ikke samme sted som hvis vi starter på samme punktet og først går 1 000 km nordover og deretter 1 000 km i rett østlig retning. Prøv på en globus og husk at rette linjer på en kuleflate er storsirkler, altså sirkler som går diametralt rundt hele jorda.
Kulekoordinater
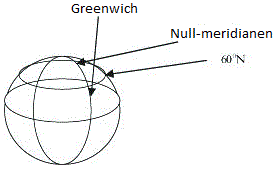
Dette betyr at kartesiske koordinater ikke er særlig smarte å bruke på jordoverflaten. Det går bra på et lite område hvor jordkrumningen ikke gir så store utslag, men på havet ville det ikke fungere. Derfor bruker man et litt annet system for koordinater. Slike koordinater som fungerer på en kuleflate kalles rett og slett kulekoordinater. Kulekoordinater er slike som brukes for å angi en posisjon på et kart eller en globus. En typisk koordinatangivelse i kulekoordinater er 58grader18,0´N, 06grader40,0´E. Dette er en by i Norge! Det første tallet er nordlig bredde. Det starter med 00graderN på ekvator og går til 90graderN på nordpolen. Tilsvarende på den sørlige halvkule. Det er altså 180 grader mellom de to polene. Fra alle steder som befinner seg på 60 grader N er det dobbelt så langt til ekvator som til Nordpolen (60 grader til ekvator og 90-60=30 grader til Nordpolen. Det andre tallet angir østlig/vestlig lengde. Her er det også 360 grader rundt hele og den såkalte null-meridianen er den storsirkelen fra Sørpolen til Nordpolen som går gjennom Greenwich-observatoriet i London.

Null-meridianen.
Dette systemet gir entydig stedsangivelse, og det er uvesentlig hvilke koordinat vi gir først, vi kommer til samme sted om vi først finner breddegraden (nord-sør) og deretter lengdegraden (øst-vest) eller motsatt.
Dette var to typer av koordinatsystemer. Begge to er laget for den verden de befinner seg i. De kartesiske koordinatene er skreddersydd for en plan flate, mens kulekoordinatene er tilpasset en kule.
Polarkoordinater
En plan variant av kulekoordinater er det som kalles polarkoordinater. Disse tar utgangspunkt i et punkt og en retning slik som de kartesiske koordinatene, men i dette tilfellet angir den ene koordinaten avstanden fra det valgte punktet og den andre vinkelen med den utvalgte retningen
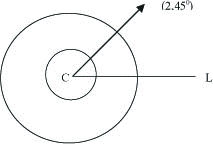
Polarkoordinater.
som betyr avstand 2 fra C og vinkel 45 grader med linja L
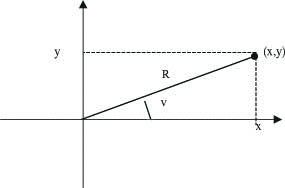
I dette systemet er første koordinat et positivt tall og den andre koordinaten er en vinkel mellom 0 og 360 grader eller 0 og 2þ målt i radianer. Dette systemet er nesten entydig, det eneste unntaket er sentrum C, som er gitt ved koordinatene (0,v) for en hvilken som helst vinkel v. Utenfor C er koordinatene entydig. Vi kan komme fra det kartesiske koordinater til polarkoordinater ved enkle regneoperasjoner. La (x,y) være de kartesiske koordinatene til et punkt og (R,v) polarkoordinatene til samme punktet
Kartesiske og polare koordinater til ett punkt.

Dermed har vi:
og den andre veien
![]()
Kartesiske koordinater passer for plan, mens kulekoordinater passer for kuler. Hva da med andre flater? Det er faktisk mulig å lage egne koordinater på mange forskjellige flater, det eneste vi trenger er en pen måte å beskrive flaten på. Når vi har det kan vi skreddersy et koordinatsystem for akkurat denne flaten. Disse koordinatsystemene har de to vesentlige egenskapene som vi har understreket flere ganger
i) Det må være hipp som happ hvilken av de to koordinatene vi måler ut først
ii) Det må være en entydig beskrivelse av hvert eneste punkt på flaten
Sylinderkoordinater
Et eksempel på slike skreddersydde koordinater er sylinderkoordinater, hvor den ene koordinaten beskriver hvor langt inn i røret vi går, mens den andre koordinaten angir en vinkel rundt røret. Et annet eksempel er det som matematikere kaller en torus.

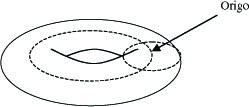
Torus.
En torus har samme form som en smultring eller et bildekk. Et koordinatsystem på en slik torus er gitt ved to vinkler, dvs to tall mellom 0 og 2þ. Vi bestemmer oss først for et punkt, origo, og en retning. Origo kan vi f.eks. legge slik det er angitt på figuren og retningen er det naturlig å ha rundt oppå toppen. Den andre retningen, vinkelrett på den første blir dermed rundt slangen, slik de to stiplede linjene angir.
Del på Facebook
Skrevet av
Institusjon
Begrep
-
Kartesisk koordinatsystem
Et koordinatsystem der aksene står vinkelrett på hverandre.
-
Sfære
En sfære er en kule og er definert som alle punktene i rommet med en fast avstand, r, fra et fast punkt.