Matematiske bevis
I enhver matematisk teori er bevis noe av det som har størst betydning. En setning eller et teorem, som det vi skal formulere her, må bevises for å ha noen mening, men hva betyr det å bevise en matematisk setning?
Et grunnleggende spørsmål i så måte er hva et bevis er. For å kunne svare på dette må man ta et skritt tilbake og si noe om hva slags vitenskap matematikk er.
I motsetning til naturvitenskapene, som forsøker å forklare og forstå naturen, går matematikk i en annen retning. Riktignok ligger mye av motivasjonen for matematikk i naturen, i naturlovene og i intuisjon knyttet til naturlige prosesser og fenomener, men matematikk er en aksiomatisk vitenskap, dvs. at all teori baserer seg på et sett av aksiomer, eller grunnsetninger. Disse grunnsetningene forsøker vi ikke å bevise, vi trenger ikke å ta stilling til om de er sanne eller ikke, vi bare sier at de utgjør vårt grunnlag og så baserer vi vår teori på det. En slik grunnsetning kan være: To vilkårlig valgte linjer er enten parallelle, sammenfallende eller så skjærer de hverandre i ett punkt. Dette aksiomet er motivert fra plangeometri, fordi vi oppfatter at det er slik geometrien er. Men når vi skal lage teorien forsøker vi ikke å bevise dette, i stedet bestemmer vi oss for at sånn er det og så bruker vi det som grunnlag for å bevise andre plangeometriske setninger. Matematikken blir på denne måten relativ og ikke absolutt; gitt følgende sett av grunnleggende antakelser (aksiomer), da gjelder slik og slik. Ett aksiom kan gjelde for en teori, men ikke for en annen. F.eks. vil aksiomet "Enhver rett (uendelig lang) linje deler planet i to deler," som passer godt i en plangeometrisk setting, ikke ha noen fornuftig motsats i romgeometri.
Et eksempel på en matematisk setning er setningen som sier at kvadratroten til 2 ikke er noe rasjonalt tall.
En matematisk setning
Det finnes tall som ikke er rasjonale (se begrepsspalten), et eksempel er løsningen av likningen . Dette tallet kalles kvadratroten til 2, .
Det aksiomatiske grunnlaget i denne sammenhengen er aksiomene for hele tall. Gitt en mengde av elementer (kalt tall) som er slik at vi har to forskjellige regler som til ethvert par av tall tilordner et annen tall (addisjon og multiplikasjon). Aksiomene krever nå at vi skal ha kommutativitet , assosiativitet (2 + (3 + 4) = (2 + 3) + 4) , distributivitet, negative tall, 0, 1 og at disse oppfyller de vanlige regnereglene. En mengde som oppfyller alle disse egenskapene og noen til kalles rasjonale tall. En av tilleggskravene er forholdstallegenskapen, for elementer og i mengden av rasjonale tall og hvor ikke er lik 0, så finnes forholdet også som element i mengden.
På dette grunnlaget kan vi ved hjelp av små skritt som er logisk sett holdbare bevise setningen over.
Bevis for setningen
Vi starter med å anta det motsatte av det vi skal bevise og viser så at da får vi ut en motsigelse. Siden verden ikke skal inneholde motsigelser kan vi fra dette slutte at antakelsen var gal.
Anta derfor at kvadratroten av 2 er et rasjonalt tall, som vi skriver og hvor vi har forkortet mest mulig (dette er helt vesentlig for bevisets gang). Dersom vi nå kvadrerer dette tallet får vi likheten , eller . Nå bruker vi en egenskap ved hele tall som sier at dersom 2 deler et produkt, så deler 2 minst en av faktorene, dvs siden deler så er delelig med 2. Vi kan derfor skrive . Setter vi dette inn i stedet for får vi og det følger at som igjen betyr at deles av 2. Men da er både og partall (delelige med 2), noe som strider mot vår antakelse, og vi har en motsigelse. Konklusjonen blir dermed at kvadratroten av 2 ikke kan skrives som et rasjonalt tall. Denne bevisteknikken kalles kontrapositiv; dette er et kontrapositivt bevis.
I de enkelte skrittene i beviset bruker vi logisk korrekte avledninger, eller implikasjoner. Vi skriver en implikasjon som en dobbelt pil ().
Et eksempel på en implikasjon er utsagnet:
er et partall er delelig med 4
I dette tilfellet har vi attpåtil en ekvivalens, altså en implikasjon begge veier, siden påstanden
er delelig med 4 er et partall.
I slike tilfeller skriver vi
er delelig med 4 er et partall
Slik er det ikke alltid. For eksempel er det sant at:
er et positivt tall er et positivt tall,
men nå er ikke den motsatte implikasjonen riktig. Vi kan ikke slutte at er et positivt tall bare fordi er positivt.
Setter vi sammen flere implikasjoner kan vi lage et direkte bevis (i motsetning til kontrapositivt, som vi kan oversette med et ”motsatt” bevis). Som et eksempel på et direkte bevis kan vi se på påstanden:
For alle hele tall , så er delelig med 10.
For å bevis dette kan vi argumentere som følger. Vi trenger bare å sjekke det siste sifferet i tallet og avgjøre om dette alltid blir 0. For er det opplagt riktig. Nå legger vi til 1 til og ser hva som skjer.
I den siste parentesen er alle tallene delelige med 5. Men mer enn det, hvis er et partall så er alle delelige med 10, og hvis er et oddetall så er også et oddetall, og summen av første og siste ledd er dermed delelig med 10. Det betyr at hele den siste parentesen alltid er delelig med 10. Men det betyr at dersom er delelig med 10, så er også delelig med 10. For stemmer det, derfor også for , men da stemmer det også for og dermed for , osv. Med andre ord - det stemmer for alle tall.
Dette er et eksempel på et direkte bevis, men det er også et eksempel på det som kalles et induksjonsbevis. Kjennetegnet for et induksjonsbevis er at dersom noe gjelder for et bestemt helt tall, og det samme alltid gjelder for tallet som er 1 større, så vil resultatet gjelde for absolutt alle hele tall (fra og med det tallet vi begynte med).
Del på Facebook
Begrep
-
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
-
Irrasjonale tall
Et reellt tall som ikke kan skrives som en brøk satt sammen av to heltall.
Eksempel: ,
-
Kontrapositiv
Av en gitt implikasjon "hvis P, så Q" kan man danne den kontrapositive implikasjonen "hvis ikke Q, så ikke P" ved å bytte om og negere premisset P og konklusjonen Q i den gitte implikasjonen. En implikasjon og dens kontrapositive er logisk ekvivalente.
Eksempel: "Et dyr som mjauer er en katt" er ekvivalent med det kontrapositive "Et dyr som ikke er en katt mjauer ikke". -
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Plangeometri
Studiet av geometriske figurer i planet. I den analytiske plangeometrien studeres plane figurer ved bruk av koordinatsystem og algebraiske metoder. Læren om kjeglesnitt er et viktig emne innenfor plangeometri.
-
Primtall
Positive hele tall større enn 1, som kun er delelig med 1 og seg selv.
Ti fem første primtallene er: 2, 3, 5, 7, 11.
-
Punkt
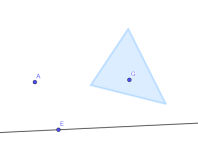
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
-
Rasjonale tall
Et tall som kan skrives som en brøk på formen der m og n er hele tall og n forskjellig fra 0. Mengden av rasjonale tall er ℚ.
Eksempel:
0,42, kan skrives som
2, kan skrives som