Pytagoras' læresetning
Det er mye morsomt man kan gjøre med vinkler og trekanter. Ut av en rettvinklet trekant kommer for eksempel en av de eldste og mest kjente matematiske læresetningene. Denne setningen har også gjort Pytagoras' navn kjent over hele verden.
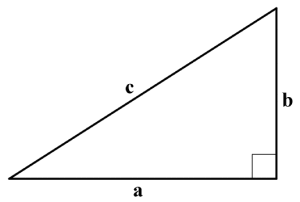
Rettvinklet trekant.
Vi skal nå se litt på rettvinklede trekanter, dvs. trekanter der en av vinklene er rett (90º). Sidene som danner den rette vinkelen kalles katetene, mens den tredje siden kalles hypotenusen. Pytagoras' setning sier at i en rettvinklet trekant er summen av kvadratene av katetenes lengder lik kvadratet av hypotenusens lengde, dvs. hvis lengdene på katetene kalles a og b og lengden på hypotenusen kalles c, må vi ha :
Hvis vi vet hvor lange to av sidene i en rettvinklet trekant er kan vi altså finne lengden av den tredje siden ved å bruke Pytagoras' setning. Setningen er derfor meget nyttig i forbindelse med for eksempel husbygging, og den brukes blant annet når vi regner ut avstanden mellom punkter og når vi regner ut arealer og volumer av diverse geometriske figurer.
Pytagoras' setning brukes også innenfor tallteori: Tegn noen rettvinklede trekanter og mål lengden på sidene. Disse lengdene er ikke så ofte hele tall. Hva hvis vi forlanger at alle sidene skal ha lengde likt et helt tall? Kan vi for eksempel tegne en rettvinklet trekant der sidene har lengder 1, 2 og 3? Ved Pytagoras' setning er dette umulig, mens for eksempel lengdene 3, 4 og 5 er mulige siden . Hvis a, b og c er positive hele tall slik at , kalles trippelet (a,b,c) et pytagoreisk trippel. Som eksempler har vi blant annet (3,4,5), (5,12,13) og (8,15,17) og multipler av disse: (6,8,10) osv. Her er fremgangsmåten for å finne alle slike tripler:
- Velg to positive hele tall A og B.
- Regn ut C = A + B, D = A + 2B.
- Regn ut trippelet (2BC, AD, B2 + C2).
Trippelet i 3) er et pytagoreisk trippel (sjekk det) og vi ser at A, B, C og D er en del av en fibonaccilignenede følge: C er summen av A og B, og D er summen av B og C.
Her passer det med et lite intermezzo om hva som skjer med de pytagoreiske triplene når eksponenten er større enn 2: På 1600-tallet satte Pierre de Fermat frem påstanden om at ligningen der n > 2 og a, b og c er positive hele tall ikke har noen løsning. I margen på Bachets oversettelse av Diofants bok "Arithmetica" skrev han at han hadde oppdaget et vidunderlig bevis for denne påstanden, men at det ikke var plass til beviset i margen. Siden den gang har matematikere jobbet for å bevise påstanden og dermed løse problemet kjent som "Fermats siste setning". På veien har nye felter innen matematikken sprunget frem, og det var Andrew Wiles som endelig ga et bevis på 1990-tallet. Beviset bruker meget avansert matematikk, og har gjort at Wiles regnes som en av nåtidens største matematikere. Han var på besøk i Norge i forbindelse med Abel-jubileet i juni 2002.
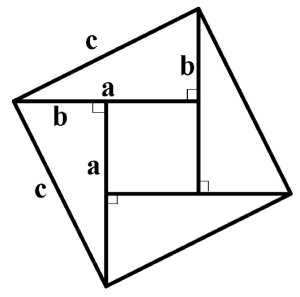
Pytagoras' setning er altså kalt opp etter Pytagoras som levde ca. 569-475 f. Kr. Men sammenhengen mellom lengdene av sidene i en rettvinklet trekant var imidlertid kjent lenge før Pytagoras' tid: Både de gamle babylonerne og kineserne kjente til og brukte setningen. For eksempel stammer følgende "hypotenus-diagram" fra Kina. Det gir et enkelt bevis for hvorfor pytagoras' setning er sann:
Hypotenusdiagram fra Kina.
Del på Facebook