Uendelighet
Hva er uendelig? Kan vi lage et symbol for uendelig og late som om det er et tall vi kan regne med på lik linje med de vanlige tallene?
En litt underlig og fantasifull matematikkhistorie går omtrent slik: Vi tenker oss to hoteller, de er så store at de har uendelig mange rom. Vi kan selvfølgelig ikke bygge slike uendelig store hoteller, men vi antar likevel at vi har gjort det (matematikere er gode til å tenke seg ting som ikke går an). Rommene i begge hotellene er nummerert 1,2,3,4, … og siden vi har uendelig mange tall sier vi at vi har nok til å nummerere alle rommene.
En dag skjer det noe leit; det ene hotellet brenner ned til grunnen. Heldigvis kommer alle gjestene seg ut og ingen blir skadet. Men det er kaldt ute, og hotellet var helt fullt, ikke et eneste ledig rom. Dessverre er det andre hotellet også fullt. Men hotelldirektøren der vet likevel råd. "Selv om mitt hotell er helt fullt skal jeg klare å innlosjere alle gjestene fra det nedbrente hotellet, bare send dem over."
Hvordan klarte hotelldirektøren dette kunststykket, å fylle opp et allerede fullt hotell med uendelig mange nye gjester? Jo, han ba alle sine gjester om å ta med seg sakene sine og gå til rommet med dobbelt så høyt nummer. Så de på rom 1 gikk til rom 2, de på rom 2 til rom 4, de på rom 3 til rom 6, osv. Siden alle flyttet på seg og hotellet hadde uendelig mange rom fant alle gjestene seg et nytt rom. Dermed ble rommene 1,3,5, ... ledige og de brann-rammede gjestene fikk beskjed om å innta rommet med nummer gitt ved å doble det gamle romnummeret og trekke fra 1. Branngjest nr. 1 fikk rom nr. 1, branngjest nr. 2 fikk rom nr. 3, branngjest nr. 3 fikk rom nr. 5, osv. Ingen gjester havnet dermed på samme rom, alle fikk plass og krisen var løst. Hvordan kan dette gå an? To stappfulle hoteller får plass på ett like stort hotell? Svaret ligger i uendelighetsbegrepet. Når vi regner med uendelig som om det var et vanlig tall kan vi omtrent få til alt mulig.
Det første spørsmålet vi stiller, er om begrepet uendelig egentlig har noen mening? Selv om det utvilsomt finnes mengder med uendelig mange elementer, tenk bare på et linjestykke, så kan vi ikke telle elementene (det ville jo ta uendelig lang tid) og da er det spørsmål om det i det hele tatt har mening å snakke om antallet elementer i slike uendelig store mengder. For matematikere har det mening, og det er faktisk nødvendig i mange sammenhenger å kunne snakke om det. Vi har nevnt antall punkter på et linjestykke og vi har sett på alle naturlige tall. Vi kan ikke fornekte disse mengdenes eksistens. Tilsvarende kan man vise at det finnes uendelig mange primtall. Slike ting tvinger oss til å forholde oss til begrepet uendelighet. Hva er så uendelig, finnes det forskjellige former for uendelighet og hvordan kan vi regne med uendelig?
For det første, siden vi har sagt at uendelig er et nødvendig begrep kan det være greit å gi det et navn, og siden 0 er opptatt har matematikere for mange hundre år siden valgt å la tegnet ∞ bety uendelig. For 0 har vi en del gode regneregler, blant annet
,
,
og ikke minst
.
For har vi færre regler. Det vi kan si er at og . Dessuten at og . Prøver vi å trekke fra får vi problemer. Subtraksjonen har rett og slett ikke mening. Svaret kan være 0, et annet tall eller . Hvis uttrykket skulle ha mening måtte det ha blitt det samme hver gang.
Det som kanskje er vel så interessant med begrepet er at det ikke er ett begrep, men mange. Det finnes flere grader av uendelig. Den minste er den som kalles tellbarhet, dvs like mange elementer som det er naturlige tall. En tellbar uendelig mengde har bare "litt" flere elementer enn en endelig mengde.
Det neste uendelighetsbegrepet er det som kalles et kontinuum, eller antallet desimaltall mellom 0 og 1, eller antall punkter på et linjestykke av endelig eller uendelig lengde. Det er nemlig lett å se at det er like mange tall mellom 0 og 1 som det er tall som er større enn 1. For hvert tall x mellom 0 og 1 kan vi se på . Dette tallet vil være større enn 1. Tilsvarende kan vi gjøre for tall y som er større enn 1, tallet ligger mellom 0 og 1. Dermed har vi laget en regel som til et hvert tall mellom 0 og 1 tilordner et tall større enn 1 og omvendt. Følgelig må det finnes like mange av dem. Man skal være litt forsiktig med dette begrepet "like mange av dem" når vi snakker om uendelig store mengder. "Like mange" er egentlig et begrep som er forbeholdt endelige mengder og det blir fort galt når vi bruker det om uendelige mengder. Ta f.eks. mengden av tall mellom 0 og 1. Det er nokså opplagt at vi kan lage en regel som tilordner et tall mellom 1 og 2 til et tall mellom 0 og 1, bare ved å legge til 1. På den annen side kan vi lage en regel som tilordner et tall mellom 0 og 2 til et tall mellom 0 og 1 og omvendt, bare ved å gange eller dele med 2. Med andre ord kan vi til en mengde av tall finne en regel som til ethvert tall tilordner et annet tall i en ekte delmengde av den opprinnelige mengden. Denne regelen går begge veier (som å gange og dele med 2 som i eksempelet over) og med all rimelighet kan vi si at det er "like mange" elementer i mengden som i en delmengde. Det høres litt sprøtt ut, ikke sant? Alle problemene baserer seg på at vi forholder oss til uendelig som om det var et begrep på lik linje med alle andre tall, noe som vi altså ikke kan gjøre.
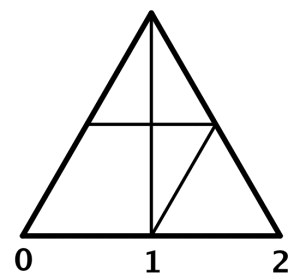
Figur 1Figur 1 viser et geometrisk argument for det samme. Den nederste linja er tallinja fra 0 til 2, mens linja i midten er like lang som tallinja fra 0 til 1, den er som vi ser parallellforskjøvet ned på den nederste tallinja. Samtidig kan vi trekke linjer fra toppunktet og ned på den nederste linja. Disse linjene tilordner et punkt på den nederste linja til et hvert punkt på den midterste linja, og omvendt. Vi kan med andre ord finne en regel som identifiserer et linjestykke med en delmengde av seg selv. Hvis dere ser nøye på dette geometriske eksemplet så ser dere at det er en illustrasjon av det vi har skrevet over. De to uendelighetsbegrepene vi har sett på er altså ikke like. For det første, hva betyr et slikt utsagn? Det betyr at vi ikke kan finne en regel som til ethvert element i en tellbar mengde tilordner et element i en kontinuumsmengde og omvendt (se artikkelen om tellbarhet).
Et veldig berømt spørsmål som matematikere har syslet med i mange år kalles kontinuumshypotesen. Det var matematikeren Georg Cantor som først stilte spørsmålet: Kan vi finne en uendelig delmengde av de reelle tallene som ligger mellom tellbar og kontinuerlig? Dvs. den skal være så stor at vi kan bevise at den ikke er tellbar, men så liten at det ikke finnes noen regel som setter den i fram-og-tilbake forbindelse med alle desimaltall mellom 0 og 1. I dag er det ingen som tror at det er mulig å lage en slik mengde, men ingen har vært i stand til å bevise det!
Del på Facebook
Tilsvarende emner behandles også i
Begrep
-
Endelige mengder
En mengde som har et endelig antall elementer, og det må i prinippet være mulig å telle antall elementer.
Eksempler: Mengden av barn i en klasse eller mengden av alle sandkorn på jorda. Mengden av naturlige tall er derimot ikke endelig.
-
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
-
Kontinuumshypotesen
Hypotesen om at det ikke finnes noe kardinaltall mellom kardinaltallene for de rasjonale tallene og de reelle tallene.
Et kardinaltall er et tall som besvarer spørsmålet "hvor mange?", som for eksempel en, to, tre osv. Kardinaltall brukes også om antall elementer i en uendelig mengde, som mengden av de rasjonale tallene eller de reelle tallene. Kardinaltallet for mengden av reelle tall er størst av disse to, men fins det noe kardinaltall mellom dem? -
Linje
En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.
-
Punkt
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
-
Tellbar
En tellbar mengde er en mengde som kan avbildes med en-til-en korrespondanse med de naturlige tallene. En ikke tellbar mengde er en uendelig mengde.
Omtalt person