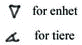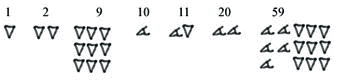Babylonsk tallsystem
Mens egypternes matematikk var praktisk rettet, viste babylonerne en teoretisk interesse for matematiske problemer. Ulempene med med det babylonske tallsystemet var blant annet at de kun hadde to tallsymboler, og ingen av disse var tallet 0.
På samme måten som Nilen i Egypt skapte Eufrat og Tigris grunnlaget for den babylonske sivilisasjonen i Mesopotamia.
Mellom år -3000 og år -2000 var det sumererne som regjerte i den sørlige delen av Mesopotamia. Deres kultur hadde nådd et høyt nivå, og deres folk var blant de første som hadde et skriftspråk. Etter hvert ble de dominert av folk fra Akkad lenger nord, som overtok mye av deres kultur. Omkring år -1800 kom kong Hammurabi fra byen Babel til makten, og han grunnla det første babylonske dynasti.
De eldste kjente tekstene fra Mesopotamia stammer fra år -3000, mens de eldste babylonske tekstene vi kjenner, er fra perioden -1900 til -1600.
Babylonsk tallnotasjon
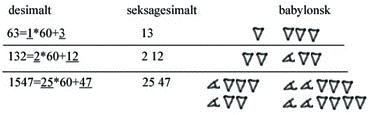
Babylonerne brukte et slags ufullstendig posisjonssystem med grunntall 60 (et seksagesimalt system). Med et fullstendig 60- talls posisjonssystem er det nødvendig med et symbol for null (den "tomme" plassen) og et symbol for hvert av de 59 tallene. Men babylonerne hadde bare to tegn:
Fra 60 av begynte de på nytt, ved å innføre en ny posisjon som skulle angi antall 60'ere osv.
Eksempel:
Som vi ser, skaper et slikt system stor tvetydighet. Er

Systemet mangler tegn for 0, komma og skikkelig posisjonsklarering.
Vår inndeling i minutter og sekunder stammer fra babylonerne. Via grekerne og araberne kom systemet til Vest-Europa ca. år 1200. (Minutt = en sekstidel (av en time) = pars minuta prima (Latin). Sekund = en sekstidel (av et minutt) = pars minuta secunda).
Regning hos babylonerne
Addisjon, subtraksjon og multiplikasjon foregikk som hos oss. Babylonerne trengte multiplikasjonstabeller over for alle tall i, j mellom 1 og 59. Divisjon foregikk slik: 47:3 ble regnet ut ved først å beregne 1/3 og deretter multiplisere med 47.
Babylonerne løste lineære og også noen ikke-lineære ligningssystemer slik vi gjør det, men de brukte ikke bokstavsymboler til å representere tall. Algebraen var retorisk, altså uttrykt med ord og setninger. Likevel var de i stand til å løse f.eks. annengradsligninger.
Et eksempel er ligningen . Babylonerne "omskrev" til (i vår notasjon):
x (x + 6) = 16
x + 6 = y
Altså får vi
xy = 16
Dette løste babylonerne slik: Sett y = a + 3, x = a - 3. Da er xy = a2 - 9 = 16, slik at a2 = 25 og dermed er a = 5. Det gir x = 2 og y = 8.
Hvis vi sammenligner babylonsk matematikk med egyptisk matematikk, kan vi si at egyptisk matematikk er mer direkte rettet mot praktiske anvendelser, mens babylonerne begynner å vise en teoretisk interesse for matematiske problemer. Babylonsk algebra representerer et stort framskritt, for ganske kompliserte ligningssystemer kan løses med den. En alvorlig ulempe er imidlertid dårlig og mangelfull matematisk notasjon.
Del på Facebook