Strekkoder

 

Melkekartong med strekkode.

"Jeg skal bare ha denne, jeg", sier du og gir en liter TineMelk Hel til ekspeditøren i butikken. Ekspeditøren drar strekkoden på melkekartongen forbi en strekkodeleser, og du hører en liten pipelyd samtidig som prisen kommer opp på skjermen i kassa. En sjelden gang kan det oppstå problemer i denne prosessen, og ekspeditøren må dermed taste inn nummeret som står under strekkoden for hånd. Strekkoden er altså tallet som står skrevet under, skrevet med streker. Tallene er forståelige for oss, strekkoden er forståelig for en strekkodeleser. De aller fleste butikker i dagens samfunn krever at leverandørene leverer produktene med strekkoder. Da har man et nummer som entydig identifiserer hvert produkt.

Den enkelte butikk har i dag en database som inneholder alle varer som selges der. Strekkoden inneholder det unike nummeret som brukes til oppslag i denne databasen. Det er i databasen at man finner informasjon om den aktuelle varen, for eksempel pris, varebeskrivelse, enhet, mengde osv. Når melkekartongen leses, slår vi altså opp i butikkens database, der butikkeieren har lagt inn prisen på melken. På en 1-liters kartong med TineMelk Hel står tallet 7 038010 000065. Dette tallet identifiserer produktet 1 liter helmelk fra Tine Meierier og har altså bare indirekte noe med prisen å gjøre.

Når du låner en bok på biblioteket er det flere strekkoder inne i bildet. En strekkode finner du bak på boka du låner. Denne følger med fra forlaget, og til dette nummeret hører ting som tittel, forfatter, opplag osv. På bokas første side finner du en annen strekkode (iallfall på de fleste bibliotek i dag). Den er plassert der av biblioteket og passer inn i bibliotekets egen database, der det ligger opplysninger om hvilken hylle boka står i, om boka er utlånt osv. En tredje strekkode involvert i et lån på biblioteket, finner du på lånekortet ditt. Dette er igjen noe biblioteket står for, og dette nummeret identifiserer deg entydig som en av bibliotekets lånere. I databasen over lånere ligger ditt navn, adresse, purringer osv.

Tanken om å gi et entydig nummer til alt mulig slo an for fullt på 1970-tallet (men vi har for eksempel hatt personnummer her i landet siden 1964, se artikkelen Personnummer). I 1973 innførte handelsnæringen i USA koden UPC (Universal Product Code) som standard strekkode for merking av sine produkter under organisasjonen UCC (Uniform Code Council). Europa fulgte snart etter, og i 1977 ble organisasjonen EAN (European Article Numbering) stiftet av handels- og industribedrifter i 12 europeiske land. EAN utvidet, og ble etterhvert hetende EAN International, representert i nær 100 land. I Norge fikk vi organisasjonen EAN Norge, stiftet i 1978, som arbeider med utvikling og vedlikehold av systemer og registerhold og forvaltning i Norge.

Den 7. juni 2005 fusjonerte UCC og EAN, og ble til GS1 (Global Standards One), og EAN Norge ble til GS1 Norway i 2006. EAN-navnet henger imidlertid fortsatt igjen på navnene på kodesystemene som brukes.

EAN videreutviklet UPC-koden, og EAN-systemet har idag to standarder, EAN 13 og EAN 8. 13 og 8 står for antall siffer som kodes. Den aller vanligste standarden er EAN 13 (EAN 8 brukes på varer med begrenset plass til stekkodesymbolet). Det brukes forøvrig flere andre typer strekkoder i Norge, for eksempel i transport og logistikk brukes Kode 128 som er en videreutvikling av EAN 13. EAN 13-koden er imidlertid den mest brukte strekkoden på forbruksvarer i Norge, og det er den vi skal se nærmere på.

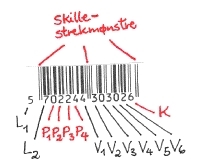
Vi skal skrive de 13 sifrene i EAN 13-koden på formen L₁L₂P₁P₂P₃P₄V₁V₂V₃V₄V₅V₆K.

L₁L₂ angir landkoden, P₁P₂P₃P₄ angir leverandør/produsent-nummeret, V₁V₂V₃V₄V₅V₆ står for varenummeret og K er kontrollsifferet.

 

EAN 13-kode.

Når vi ser en EAN 13-kode, står sifferet L₁ til venstre, foran selve strekkoden. Dette sifferet er ikke strekkodet, men er likevel en del av koden. Vi skal se at L₁ bestemmer og er bestemt av hvordan de andre sifrene kodes. De resterende 12 sifrene er delt i to blokker med 6 sifre i hver. Blokkene er omgitt av tre skille-strekmønstre (visuelt har disse litt lengre streker).

L₁L₂: EAN har en tabell for landkodene. For Norge er koden 70, hvilket betyr at hvis en strekkode starter med 70, er den utstedt i Norge (selve produktet trenger ikke være produsert i Norge). Du kan også finne 20-29 som landkode på produkt dersom det er produsert i Norge (for eksempel finner du det på Kokt Skinke fra Gilde). I EANs landkodetabell er 20-29 såkalte "Butikkfunksjoner". Landkoden kan også ha tre sifre, men da er enten produsent- eller varenummeret kortere. L-ene, P-ene og V-ene utgjør alltid 12 sifre i en EAN 13-kode.

P₁P₂P₃P₄: Leverandør/produsent-nummeret utdeles av den nasjonale EAN-medlemsorganisasjonen (EAN NORGE hos oss). Hvis en produsent ikke har så mange produkter, kan EAN utstede et lengre produsentnummer, slik at man har mindre plass til varenummerne. Dette kan gjøres for å gi EAN flere tallkombinasjoner å bruke på produsentene, og er dermed en mer effektiv bruk av koden.

V₁V₂V₃V₄V₅V₆: Varenummeret bestemmes av produsenten, som kan velge fritt så lenge alle varene med samme produsent har et unikt varenummer (man må for eksempel skille mellom en liter helmelk og en halv liter helmelk).

K: Kontrollsifferet er også strekkodet og regnes ut fra de andre sifrene i koden. K brukes til å kontrollere at strekkodeleseren har lest riktig. Det kan ha oppstått riper i strekkoden o.l., og da er det greit å ha en kontroll. Det er også derfor sifrene må stå under strekkoden slik at de eventuelt kan tastes inn manuelt. For å finne kontrollsifferet regner vi først ut kontrollverdien, som regnes ut fra formelen

L₁+3L₂+P₁+3P₂+P₃+3P₄+V₁+3V₂+V₃+3V₄+V₅+3V₆.

Kontrollsifferet er det sifferet vi må legge til kontrollverdien for å få et tall som er delelig med 10 (når vi skal ha ut et siffer regner vi alltid modulo 10). Hvis utregningen av kontrollsifferet stemmer med avlesningen av K, er det meget stor sannsynlighet for at avlesningen er korrekt.

La oss ta TineMelk Hel som eksempel. Strekkoden er 7 038010 000065. Siden koden starter med 70, betyr det at EAN NORGE har fastsatt produsentnummeret, som for Tine er 3801. Dermed kan Tine bestille strekkoder til produktene sine der alle kodene starter med 7 03801. Varenummeret til helmelken er 000006. Kontrollverdien er

7 + 3·0 + 3 + 3·8 + 0 + 3·1 + 0 + 3·0 + 0 + 3·0 + 0 + 3·6 = 55

Hvis vi legger til sifferet 5, får vi 60, som er delelig med 10, så K=5, noe som stemmer. Nå kan du for eksempel sjekke brunosten og yoghurten også.

Vi har allerede sett litt av matematikken som fins på melkekartongen, og nå skal vi se mer. Hvordan kan vi skrive tall ved å bruke streker og mellomrom? For å forklare dette skal vi bruke tallet "1" til å representere en enkel strek og tallet "0" for et enkelt mellomrom. For eksempel betyr "11101" en trippel strek etterfulgt av et enkelt mellomrom og en enkel strek.

 

11101 – trippel strek, enkelt mellomrom og enkel strek.

Bredden "enkel" varierer litt, avhengig av maskinen som trykker strekkoden, men det er de relative avstandene som teller, så hvis det hele forskyves gjør ikke det noe. Men det er to kriterier: Det må være nok avstand til at leserne kan skille strekene, og strekkoden skal ikke ta for stor plass. Vanligvis er bredden på hele strekkoden mellom 10,4 og 24 mm.

En EAN 13 strekkode har som nevnt tre skille-mønstre (streker som er litt lengre enn de andre). Det første skillet er strekkoden 101, det midterste er 01010, og det bakerste er 101. Alle EAN 13-koder har disse skillene.

Vi sa også tidligere at L₁ ikke er strekkodet, men bestemmer og er bestemt av hvordan de andre sifrene er kodet. La oss kalle blokken L₂P₁P₂P₃P₄V₁ for den venstre blokken og V₂V₃V₄V₅V₆K for den høyre blokken. Alle sifrene i den venstre blokken kan kodes på to forskjellige måter. L₁ bestemmer hvilken av disse måtene hvert av sifrene i den venstre blokken skal kodes på. Her kommer tabellene for å kode de 13 sifrene med 1-ere (streker) og 0-ere (mellomrom):

 

Siffer	Venstre blokk	Venstre blokk	Høyre blokk
	Ulike	Like
0	0001101	0100111	1110010
1	0011001	0110011	1100110
2	0010011	0011011	1101100
3	0111101	0100001	1000010
4	0100011	0011101	1011100
5	0110001	0111001	1001110
6	0110001	0000101	1010000
7	0111011	0010001	1000100
8	0110111	0001001	1001000
9	0001011	0010111	1110100

Tabell 1.

For å vite om vi skal kode sifrene i venstre blokk med "Ulike" eller"Like" kode, bruker vi L₁, og leser av i tabell 2.

 

L1	L2	P1	P2	P3	P4	P5
0	Ulike	Ulike	Ulike	Ulike	Ulike	Ulike
1	Ulike	Ulike	Like	Ulike	Like	Like
2	Ulike	Ulike	Like	Like	Ulike	Like
3	Ulike	Ulike	Like	Like	Like	Ulike
4	Ulike	Like	Ulike	Ulike	Like	Like
5	Ulike	Like	Like	Ulike	Ulike	Like
6	Ulike	Like	Like	Like	Ulike	Ulike
7	Ulike	Like	Ulike	Like	Ulike	Like
8	Ulike	Like	Ulike	Like	Like	Ulike
9	Ulike	Like	Like	Ulike	Like	Ulike

Tabell 2.

Hvis vi ser på melkekartongen igjen er P₂ = 8. Siden L₁ = 7, skal P2 kodes med "Ulike" kode, og P₂ blir derfor 0110111 i strekkode. Kan du skrive ned hele strekkoden til Tine Melk Hel med 0-ere og 1-ere? Se om det stemmer med strekene på kartongen. Her har vi tegnet helmelk-koden på et millimeterark ved å bruke tabellene over:

Koden for helmelkkartongen.

 

Strekene er altså tall som en strekkodeleser forstår. En slik leser er ofte en laser som kan lese slike tall på flere meters avstand. Alle typer strekkoder har tilsvarende tabeller som vi har sett for EAN 13. Disse tabellene blir lagt inn i datautstyret som produserer og leser kodene.

Vi kan gjøre følgende observasjoner fra tabellene:

1. Hvert siffer bruker 7 plasser i strekmønsteret og består av to streker og to mellomrom.
2. Strekene og mellomrommene kan altså ha bredde tilsvarende 1, 2, 3 eller 4 plasser.
3. Alle sifrene i den venstre blokken starter med 0 og alle sifrene i den høyre starter med 1.
4. For hvert siffer er mønstrene under "Høyre blokk" og "Venstre blokk Ulike" like, men med 1-ere byttet ut med 0-ere og vice versa.
5. For hvert siffer får vi mønsteret "Venstre blokk Like" ved å lese "Høyre blokk"-mønsteret fra høyre mot venstre.
6. L₂ er alltid kodet med "Ulike" kode.
7. Når L₁ er forskjellig fra 0, er alltid tre tall i venstre-blokken kodet med "Like" kode og de tre andre med "Ulike" kode.

Dette er altså innmaten i EAN 13-strekkoden. Det er matematikken som får den til å virke:
La oss se på observasjon 1). Sagt på en annen måte sier denne at vi ser på kombinasjoner av fire tall (som representerer to streker og to mellomrom) som kan være 1, 2, 3 eller 4 (som representerer antall plasser, eller tykkelsen på streken eller mellomrommet) der summen av dem skal være 7 (totalt antall plasser). Da kan vi for eksempel ha kombinasjonen 1 1 1 4. Observasjon 2), 3) og 4) sier videre at om vi leser kombinasjonen fra høyre, dvs. 4 1 1 1, skal dette telle som samme kombinasjon. Hvor mange forskjellige kombinasjoner kan vi ha? Jo, vi kan ha nøyaktig 10 (og vi skal jo kode 10 sifre!):

 

Kombinasjon	Siffer
1 1 1 4	6
1 4 1 1	3
1 1 2 3	0
1 1 3 2	4
1 2 1 3	8
1 2 3 1	5
1 3 1 2	7
2 1 1 3	9
1 2 2 2	1
2 1 2 2	2

Videre skal altså L₁ bestemme hvilken paritet sifrene i venstre blokk skal kodes med. Også dette kan sies matematisk:
La L₁ være forskjellig fra 0. Hvis vi ser på sifrene P₁, P₂, P₃, P₄ og V₁, skal vi ha to forekomster av "Like" (ved observasjon 5) og 6)). Vi skal altså ha kombinasjoner av minst to og høyst fem tall som kan være 1, 2 eller 3 og der summen av dem er 5. Dessuten må vi ha at når vi summerer annenhvert tall må denne summen være mindre eller lik 3.

Dette gir følgende kombinasjoner:

 

Kombinasjon	L1
2 3	forekommer ikke
3 2	6
1 2 2	4
2 2 1	5
1 3 1	3
1 1 1 2	1
2 1 1 1	9
1 1 2 1	8
1 2 1 1	2
1 1 1 1 1	7

En strekkode er ikke noe mer mystisk enn en metode å skrive tall (og bokstaver) på. Metoden bruker streker, mellomrom, avstand og tykkelse på disse i forhold til hverandre og matematikk: Vi ser at de ulike tallene brukt i metoden (7 plasser, 2 streker, 2 mellomrom osv.) gir oss akkurat nok kombinasjoner til å bruke i kodingen.